ทฤษฎีบท พีทาโกรัส คิดเร็ว 5 วินาทีได้จริงหรอ? คณิต ม.2

ทฤษฎีบทพีทาโกรัส กล่าวไว้ว่า...

เรื่องนี้เป็นเรื่องที่เราจะประยุกต์สมการการหาความยาวด้านกับ ''สามเหลี่ยมมุมฉาก'' เพราะฉะนั้นจำไว้เลยครับน้อง ว่าถ้าเราเจอโจทย์ที่เกี่ยวกับสามเหลี่ยมมุมฉากเมื่อไหร่ ให้นึกถึงทฤษฎีบทพีทาโกรัสก่อนเป็นอย่างแรกๆ เลย ในทางกลับกัน หากน้องเจอสามเหลี่ยมแต่มันไม่ใช่มุมฉาก ก็ไม่ต้องมานึกถึงทฤษฎีบทพีทาโกรัส

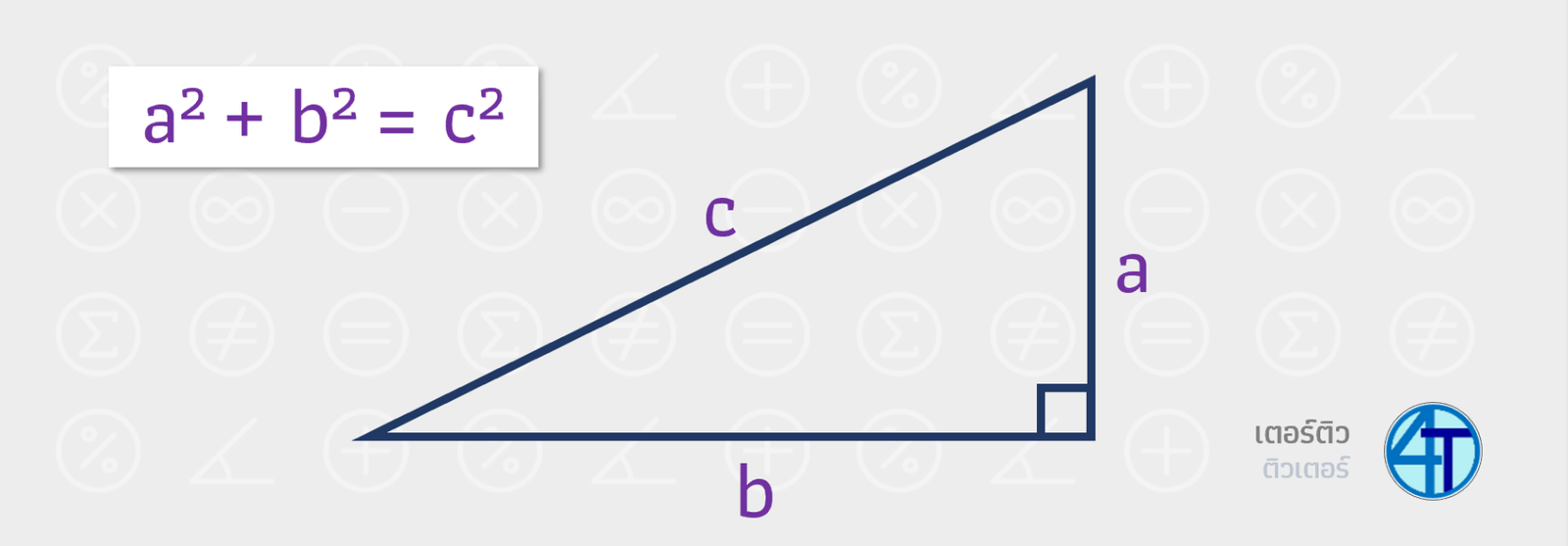
จากรูปด้านบนน้องจะเห็นว่า พี่มีสามเหลี่ยมมุมฉากอยู่ 1 อันประกอบไปด้วยด้าน 3 ด้านได้แก่ \(a,b,c\) ซึ่งโดยปกติแล้ว เรานิยมแทน \(c\) เป็นด้านตรงข้ามมุมฉาก (ด้านที่ยาวสุดของสามเหลี่ยม) ส่วนด้าน \(a,b\) เนื่องจากมันติดกับมุมฉากเลย เราจึงเรียกสองด้านนี่ว่า ด้านประกอบมุมฉาก

พีทาโกรัสกล่าวว่า ''ผลรวมของ(ด้านประกอบมุมฉากกำลังสอง) = ด้านตรงข้ามมุมฉากกำลังสอง'' ซึ่งจากภาพด้านบนก็คือ \(a^2+b^2=c^2\) สมการนี้สมการเดียวเลยน้องที่ต้องจำ! เราเรียกมันว่า สูตรพีทาโกรัส

ตัวอย่างการใช้สมการทฤษฎีบทพีทาโกรัส

ตั้งสมการได้ว่า \(x^2\,=\,1^2\,+\,1^2\) ได้ว่า \(x^2\,=2\) ซึ่งจากที่เรารู้ว่ามันหารากที่สอง ที่ลงตัวไม่ได้ น้องก็ติดรากที่สองได้เลยเป็น \(x=\pm\sqrt{2}\) แต่! เราเอาแค่ค่าบวกเพราะมันเป็นความยาวด้านสามเหลี่ยม ดังนั้นตอบแค่ \(x=\sqrt{2}\)

เสริมน่ารู้: \(\sqrt{2}\) คือ ค่าคงที่พีทาโกรัส (pythagoras constant) ซึ่งเป็นจำนวนอตรรกยะแรกที่ถูกค้นพบขึ้นบนโลก

ที่มาจริงๆ ของทฤษฎีบทพีทาโกรัส

เอาจริงๆ แล้วที่มาของสมการพีทาโกรัสนั้นมาจาก พื้นที่ของสี่เหลี่ยมจัตุรัส น้องๆ ลองดูตามรูปข้างล่างเลย คือพีทาโกรัสเนี่ย เค้าบอกว่าหากเรามีสามเหลี่ยมมุมฉาก ให้เราลองวาดสี่เหลี่ยมจัตุรัสของแต่ละด้านดังรูป

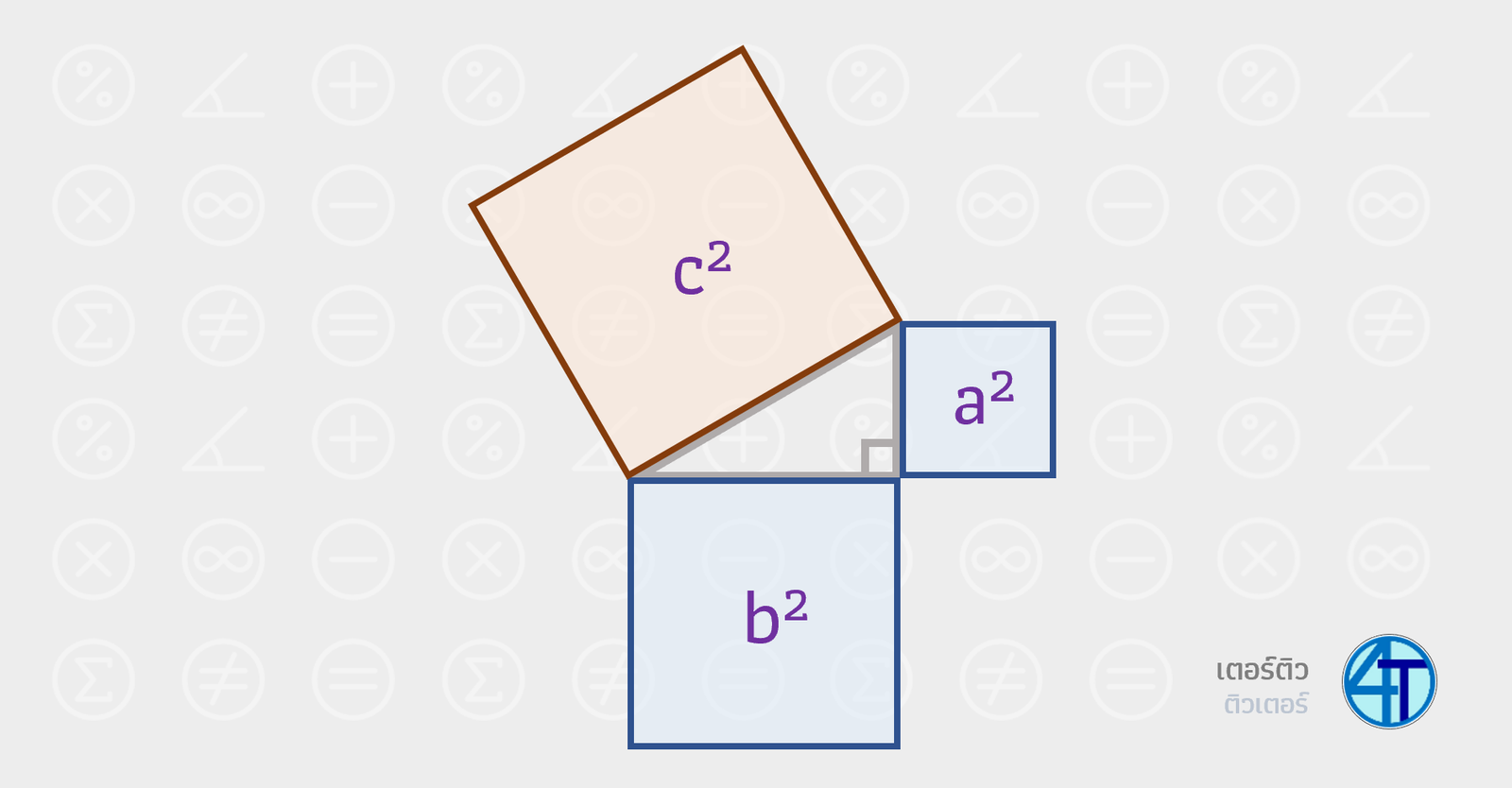
พีทาโกรัสบอกว่า พื้นที่สี่เหลี่ยมของด้านประกอบมุมฉากรวมกัน มีค่าเท่ากับ พื้นที่สี่เหลี่ยมด้านตรงข้ามมุมฉาก (พื้นที่สี่เหลี่ยมก็คือ ด้านกำลังสอง นั่นเอง)

ด้านสามเหลี่ยมมุมฉากที่เจอบ่อยควรจำได้!

เพื่อความรวดเร็วในการทำข้อสอบตั่งต่าง พี่แนะนำว่าสามเหลี่ยมมุมฉากหลักที่น้องควรจำได้มีดังต่อไปนี้ครับ ด้านบนคือ ควรจำอย่างสูงสุด ส่วนใครมีเวลาเพิ่มก็จำทีเหลือข้างล่างได้ เอาตรงๆ คือเวลาเราฝึกทำโจทย์ยิ่งมากเข้าๆ พวกนี้มันจะซึมซับไปในหัวน้องๆ เองเลย เพราะมันเจอบ่อยมาก

คิดด้านที่เหลือพีทายังไงให้เร็ว 5 วินาที

อันนี้ไม่ได้โม้นะน้อง แต่เป็นทริคดีๆ ที่พี่จะเอามาให้น้องดูกันว่าปกติแล้ว ถ้าเราเจอด้านแปลกๆ ของพีทาโกรัสเนี่ย เราจะสามารถหาด้านที่เหลือยังไงได้แบบเร็วๆ ก่อนแรกเลยน้องต้องทำโจทย์บ่อยๆ ให้พอจำได้และว่า ด้านสามเหลี่ยมมุมฉากอย่างง่ายคืออะไร เช่น \((3,4,5)\) หรือ \((5,12,13)\) ไรแบบนี้ คือถ้าพี่ให้สามเหลี่ยมมาและมีด้านยาว \(5\) กับ \(13\) น้องต้องคิดได้ใน 1 วินาทีเลยว่า อีกด้านคือ \(12\)

ต่อมาให้สังเกตแพทเทิร์นกันก่อน สมมติว่าพี่มี \((3,4,5)\) ลองนำด้านไปคูณตัวเลข คูณทุกด้านเท่าๆกัน

• \((3,4,5)\textcolor{blue}{\times 2}\) ได้ \((6,8,10)\)
• \((3,4,5)\textcolor{blue}{\times 3}\) ได้ \((9,12,15)\)
• \((3,4,5)\textcolor{blue}{\times 4}\) ได้ \((12,16,20)\)

หากน้องทำการเช็คสามเหลี่ยมใหม่ที่ได้จากการคูณ ทั้งหมดเป็นสามเหลี่ยมมุมฉาก ดังนั้นในทางกลับกันหากน้องมีสามเหลี่ยมมุมฉาก แต่ด้านที่น้องเจอ มันไม่ใช่ด้านอย่างต่ำ เราสามารถหา หรม. เพื่อตัดทอนเป็นด้านอย่างต่ำก่อนได้ และค่อยคูณกลับ

หากยังรู้สึกงงอยู่ มาดูตัวอย่างกันเลย

จากตัวอย่างให้หาค่า \(x\) หากบางคนไม่มีวิธีลัดก็คิดไปสิน้องตั้งสมการ \(x^2+\,15^2\,=\,39^2\) ย้ายข้างไปมาได้ \(x=\sqrt{39^2-15^2}=\dots\) เสียเวลาทำข้อสอบไปอีกถูกม้ะ กว่าจะมายกกำลังสองของ 39 นู่นนี่ แล้วพอลบได้น้องจะได้ \(x=\sqrt{1296}\) เอ่อะ.. เท่าไหร่หละพี่! ต้องไปถอดรากต่ออีก 5 นาทีกว่างี้ (แอบใบ้ให้ว่าข้อนี้ตอบ \(x=36\))

เนื่องจากเราจะทำข้อสอบแบบสายฟ้าแลบ วิธีข้างบนไม่เวิร์คแน่ๆ ดังนั้นมาดูวิธีดีๆ กันดีกว่า

เราลองสังเกตดูสิครับว่า \(39\) กับ \(15\) มันยังไม่ใช่อัตราส่วนอย่างต่ำนะ เพราะว่า หรม. ของ \(39\) กับ \(15\) คือ 3 ดังนั้นเราหารทุกด้านด้วย 3

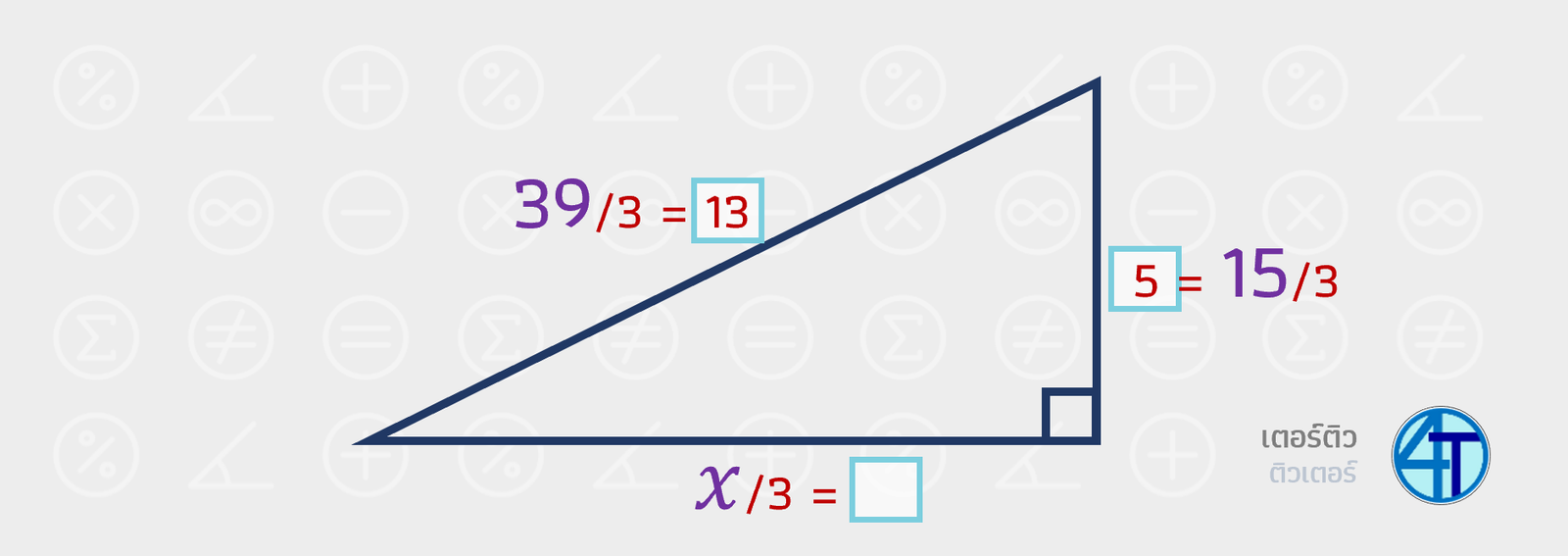
สังเกตในกล่องสี่เหลี่ยมสีเขียวนะ เลขที่เราหารได้ คุ้นๆ กันมั้ยเอ่ย ใช่แล้วน้อง มันคือด้าน \((5,12,13)\) ที่เราคุ้นเคยกันนั่นเอง ดังนั้นตอนนี้เรามี \(5\) กับ \(13\) แล้ว ด้านที่เหลืออีกด้านต้องเป็น \(12\) อย่างแน่นอน ดังนั้นเติม \(12\) ในช่องว่างกันได้เลย

ยังตอบเลยไม่ได้นะน้อง ต้องระวังนิดนึง เราจำได้มั้ยว่าเราเอา \(x\) มาหารด้วย 3 อยู่ ดังนั้น สมการที่เราต้องใช้คือตามอันล่างสุดในรูปเลย \(\frac{x}{3}=12\) ฉะนั้นตอบ \(x=12\times 3=36\) ตรงตามวิธีปกติที่คิดข้างบนเลย

โจทย์แนวนี้มีตัวอย่างเพิ่มให้ดูในวิดีโอโจทย์ประยุกต์พีทาโกรัสนะครับน้องๆ

ประยุกต์ใช้สูตรเพื่อหาความยาวด้านสามเหลี่ยม (แบบฝึกหัด)

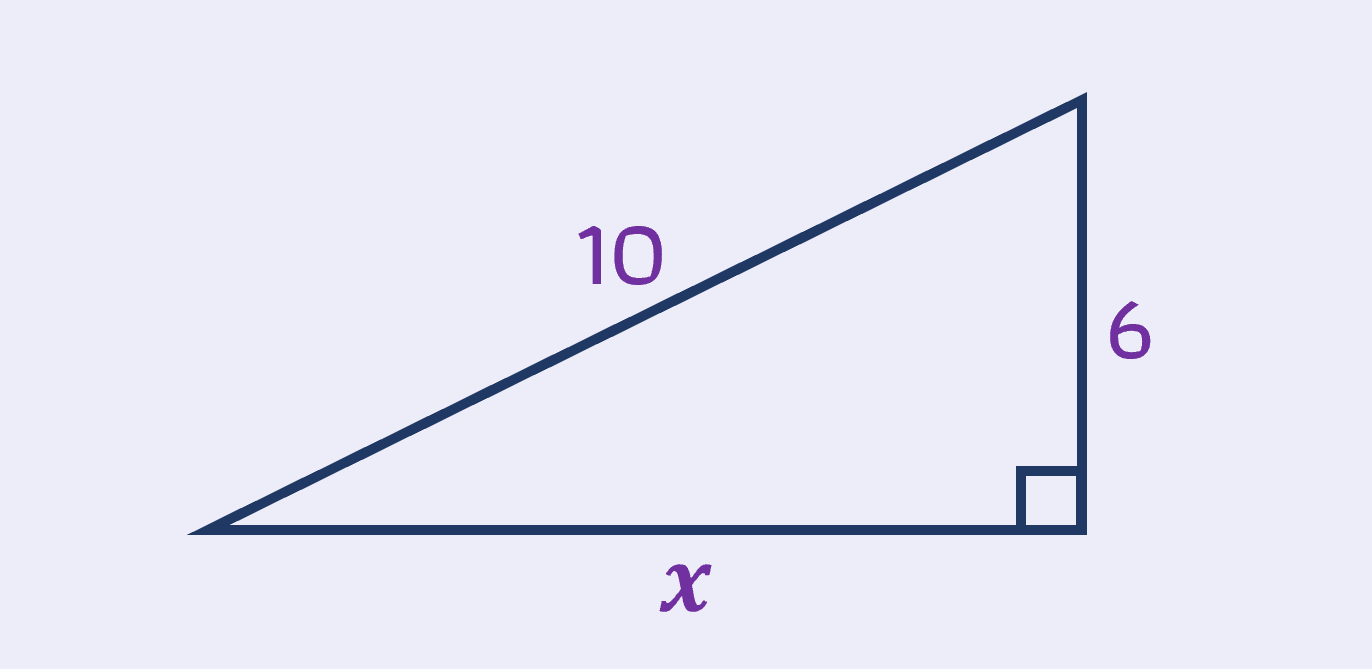
ในแต่ละข้อจงหาความยาวด้าน \(x\)