จํานวนตรรกยะ และ จํานวนอตรรกยะ กับ จำนวนจริง ม.2

เกริ่นนำ

หากเราพูดถึงคณิตศาสตร์ สิ่งที่น้องจะเจอเลยก็คือตัวเลข ดังนั้นในบทนี้ เราจะมาเรียนกันว่าตัวเลขมีแบบไหนบ้าง

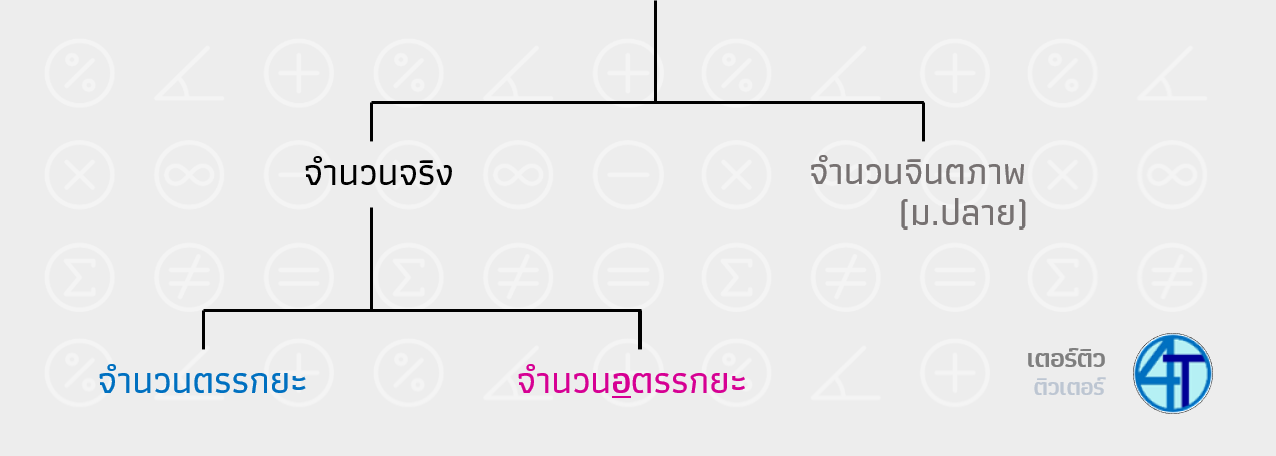
ลองดูแผนภาพด้านบนประกอบกันไปนะครับน้อง ๆ สังเกตว่าในช่วงม.ต้นที่เราเรียนกันอยู่นี้ เราจะเรียกจำนวนทั้งหมดว่า จำนวนจริง เช่น 1, 3.4, 5.34343434..., และอื่นๆ แต่หากน้องสังเกตทางด้านขวาของจำนวนจริง จะเห็นว่า จริงๆ แล้วมันก็มี จำนวนไม่จริง ด้วย เอ๊ะพี่ ไม่จริงยังไง? ในส่วนนี้น้องจะได้เรียนกันตอน ม.5-ม.6 เค้าเรียกว่า จำนวนจินตภาพ ครับน้อง ๆ

ดังนั้นตอนนี้เราสนใจกันแค่ จำนวนจริง ของเราก่อนก็พอ สิ่งที่น้องต้องรู้คือ จำนวนจริง ถูกแบ่งออกเป็น 2 กลุ่ม ได้แก่ จำนวนตรรกยะ และ จำนวนอตรรกยะ ให้สังเกตคำว่า อ- ไว้ดีๆ นะ อ- แปลว่า ไม่ ดังนั้น ทั้งสองกลุ่มนี้ก็คือ ตรงกันข้ามกัน นั่นเอง

จำนวนตรรกยะ

จำนวนตรรกยะ คือ จำนวนที่ มันเขียนในรูปของเศษส่วนได้ แต่แต่แต่ มันมีข้อจำกัดด้วยครับ คือ เศษส่วนที่เขียนออกนี้ สมมติให้เป็น \(\dfrac{A}{B}\) ทั้ง \(A\) และ \(B\) ต้องเป็นจำนวนเต็ม และตามหลักคือ เราไม่สามารถเอาอะไรหารด้วย 0 ได้ เพราะฉะนั้น \(B\neq0\) [ตัวส่วนไม่เป็นศูนย์]

และมันมีจำนวนกี่แบบครับพี่ที่เป็นจำนวนตรรกยะ? 2 แบบครับ

1. จำนวนเต็ม

เช่น \(-5, 7, 19, 256\) จำนวนพวกนี้ก็เป็นจำนวนตรรกยะครับ พี่แต่มันไม่ได้เป็นเศษส่วนนะ? ใช่น้อง แต่ จำนวนเต็มทุกตัว สามารถเขียนเป็นเศษส่วนได้ ด้วยการนำไปหารด้วย 1 เช่น \(-5=\dfrac{-5}{1}\), \(19=\dfrac{19}{1}\), หรือ \(256=\dfrac{256}{1}\) ดังนั้นมันจึงจัดเป็นจำนวตรรกยะด้วยนั่นเอง

2. ทศนิยมซ้ำ

ทศนิยมซ้ำ ยกตัวอย่างเช่น \(6.7878787878787878\dots\) ไปเรื่อย ๆ น้องจะสังเกตเห็นว่า ทศนิยมหลังจุดนั้นซ้ำ \(78\) ไปเรื่อย ๆ ไม่รู้จบ แบบนี้แหละครับที่เราเรียกว่าทศนิยมซ้ำ

แต่การซ้ำของทศนิยมนั้น ไม่จำเป็นต้องซ้ำตั้งแต่ตัวแรกก็ได้ เช่น \(10.43207207207207\dots\) จะเห็นว่าเลขนี้ ตอนเริ่มมาหลังทศนิยม มันไม่ได้ซ้ำตรง \(43\) แต่พอเริ่มเป็น \(207\) มันเริ่มซ้ำกันไปเรื่อยๆ \(207\;207\;207\;\dots\) ดังนั้นการซ้ำไม่จำเป็นต้องซ้ำตั้งแต่ตัวแรกนะครับ แต่สุดท้ายต้องมีช่วงหนึ่งแหละที่เริ่มซ้ำ

ตัวอย่างเดิมครับ น้อง ๆ มี \(6.787878787878\) เรารู้และว่า \(78\) มันคือตัวที่ซ้ำ เราจะนำเครื่องหมายขีดไปใส่ด้านบนและตัดตัวซ้ำที่เหลือออกไป จะได้ \(6.787878787878... = 6.\overline{78}\)

ส่วน \(10.43207207207\) ก็จะได้เป็น \(10.43\overline{207}\) เพราะ \(43\) ไม่ได้ซ้ำ ดังนั้นเครื่อง ขีดด้านบน เราก็จะอยู่แค่ส่วนที่ซ้ำ ซึ่งก็คือ \(207\)

** ในหนังสือเรียนมักจะเขียนแทนด้วย จุดด้านบนปิดหัวท้าย เช่น \(10.43\overline{207}\) = \(10.43\dot{2}0\dot{7}\) ซึ่งก็ถือว่าใช้ได้เหมือนกัน

เพิ่มเติม แล้วจำนวนที่ไม่ใช่ทศนิยมซ้ำล่ะพี่? เช่น 6.25, 1.281 พวกนี้ก็เป็นตรรกยะเหมือนกันครับน้อง ๆ เพราะมันคือจำนวนทั้งหมด หารด้วย 10, 100, 1000, 10000, ... นั่นเอง สังเกตดี ๆ \(6.25=\dfrac{625}{100}\) และ \(1.281=\dfrac{1281}{1000}\) นั่นเอง ในหนังสือเรียนเค้าจะสอนน้อง ๆ ว่า เลขพวกนี้เป็น ทศนิยมซ้ำศูนย์ มองภาพง่าย ๆ คือ \(6.25=6.2500000...=6.25\overline{0}\)

ทีนี้คำถามคือ ถ้า ทศนิยมซ้ำเป็นจำนวนตรรกยะ มันก็ต้องเขียนในรูปเศษส่วนได้เสมอใช่หรือเปล่าครับ? ถูกต้องแล้ว ดังนั้นในพาร์ทต่อไปเราจะมาดูกันว่า เปลี่ยนทศนิยมซ้ำเป็นเศษส่วน ทำอย่างไร

เปลี่ยนทศนิยมซ้ำเป็นเศษส่วน

เรื่องนี้หากเป็นคำพูดอาจจะเข้าใจยากกว่าวิดีโอ ดังนั้นพี่จะแปะวิดีโอประกอบไว้ด้วย หากน้อง ๆ มีเวลาแนะนำให้ดูทางวิดีโอจะได้เห็นภาพมากขึ้นครับ

ในคลิปวิดีโอ พี่จะเล่าจากหลักการและวิธีปกติก่อน จากนั้นจะนำไปสู่สูตรสรุปและการนำไปใช้และกันนะ ให้น้องเข้าใจที่มาก่อน ไม่จำสูตรอย่างเดียว เพราะสอบปุ๊บเดี๋ยวก็ลืม หลักการของเราก็คือ เราจะใช้ความ "ซ้ำไม่รู้จบ" ของจุดทศนิยมนี้แหละมาช่วย

แต่ในเว็บที่เขียนนี้ พี่จะขอข้ามไปที่สูตรและหลักการใช้กันเลย เนื่องจากการอธิบายที่มา วิดีโอสามารถครอบคลุมได้มากกว่า ดังนั้น ใครสนใจก็จิ้มที่วิดีโอด้านบนหน้านี้กันได้เลยนะครับ

สูตรที่เราจะใช้กันคือ

เลขหน้าทศนิยมเราจะไม่สนใจนะ ก็คือตัดทิ้งไปเลย แล้วค่อยนำมาตอบด้วยกันกับคำตอบที่เราหาได้ ตัวอย่าง สมมติพี่มี \(9.707070707...\) ซึ่งมันก็คือ \(9.\overline{70}=9+0.\overline{70}\) เราจะคิดแค่ส่วน \(0.\overline{70}\) จากนั้นก็จะนำเลข \(9\) มาต่อตอนตอบเป็นจำนวนคละ ดังนั้นหลังทศนิยมทั้งหมด คือ \(\textcolor{green}{70}\) และ ตัวไม่ซ้ำ ไม่มี (เป็น 0) เพราะขีดด้านบนมันครอบคลุมทั้งหมด แสดงว่า ตัวไม่ซ้ำ เป็น 0 ตัว และตัวซ้ำมีทั้งหมด 2 ตัว เพราะมันซ้ำ \(70\) ซึ่งมี 2 หลัก

ดังนั้นใส่สูตรได้เป็น \(9.\overline{70}=9\dfrac{\textcolor{green}{70}-\textcolor{purple}{0}}{\textcolor{blue}{99}}\)

ลองดูอีกหนึ่งตัวอย่าง สมมติมี \(1.5667667667...\) เขียนอีกแบบว่า \(1.5\overline{667}\)

ตัวอย่างด้านบน เรารู้ว่า หลังทศนิยมทั้งหมดคือ \(\textcolor{green}{5667}\) แต่ต่างขากข้อที่แล้วตรงที่คราวนี้เรามีตัวไม่ซ้ำ ซึ่งคือ \(\textcolor{purple}{5}\) ดังนั้น จำนวนตัวที่ซ้ำคือ 3 ตัว เพราะ \(667\) ซ้ำและมี 3 หลัก ส่วนที่ไม่ซ้ำ มี 1 ตัว

ดังนั้นแทนได้ดังนี้ \(1.5\overline{667}=1\dfrac{\textcolor{green}{5667}-\textcolor{purple}{5}}{\textcolor{blue}{999}\textcolor{deeppink}{0}}\)

จํานวนอตรรกยะ

แล้วอะไรหล่ะที่เขียนในรูปเศษส่วนไม่ได้? เราบอกกันไปแล้วในหัวข้อที่แล้วว่า หากเป็นทศนิยมซ้ำ จะเขียนในรูปเศษส่วนได้เสมอ ดังนั้น การที่เขียนไม่ได้ ก็คือเป็น ทศนิยมไม่ซ้ำ นั่นเอง แล้วมันมีอะไรบ้าง? ตามมาดูกันครับ

ที่น้องจะได้เจอบ่อยๆ ก็คือพวก ราก (เช่น รากที่สอง, รากที่สาม ตัวที่มันหาค่าลงตัวไม่ได้) เราจะได้เรียนกันในพาร์ทรากที่สอง กับรากที่สามอีกที แบบละเอียด และน้องจะเห็นเลยว่า มันเป็นตัวเลขทศนิยมที่ไม่ซ้ำไม่รู้จบ ข้อควรระวัง: บางรากก็สามารถหาค่าที่ลงตัวได้ ไม่จำเป็นต้องเป็นอตรรกยะเสมอไป นะครับ

อีกอันที่เจอบ่อยมากในคณิตศาสตร์ก็คือ \(\pi\) เพื่อนรักของเรานั่นเอง ใช่แล้วครับ ค่า \(\pi\) โดยประมาณ 3.14 แต่จริง ๆ แล้ว \(\pi\) เป็นทศนิยมไม่ซ้ำ