เลือกอ่านตามหัวข้อ?
เข้าหาบทความพี่ง่ายๆ จาก Google


แผนภาพเวนน์ ออยเลอร์ คืออะไร
แผนภาพเวนน์ ออยเลอร์ คือ การเขียนแทนเซตด้วยแผนภาพ นั่นเอง ปกติเราจะเขียนเป็นแบบ \(A=\{1,2,3\}\) เราก็สามารถที่จะเขียนเซต \(A\) เป็นแบบภาพ เพื่อให้มองง่ายขึ้นได้เหมือนกัน ดังรูปข้างล่างเลย เพื่อให้เข้าใจง่ายขึ้น สมมติว่า \(\mathbb{U}=\{1,2,3,4,5\}\)

\(\mathbb{U}\) = เอกภพสัมพัทธ์
น้อง ๆ จะสังเกตว่า ในวงกลม \(A\) มีเลข 1, 2, และ 3 อยู่ก็หมายความว่า 1, 2, และ 3 \(\in A\) ส่วนตัวที่อยู่นอกวงกลม \(A\) ก็คือ ตัวที่อยู่ใน เอกภพสัมพัทธ์ หรือ ขอบเขตที่เราสนใจ แต่ไม่ได้อยู่ในเซต \(A\) นั่นเอง
จริง ๆ แผนภาพเวนน์ฯ สามารถเขียนเป็นรูปทรงปิดอะไรก็ได้เลย แต่ส่วนมาก 99.99% มักนิยมเขียน
เซต เป็น วงกลม
เอกภพสัมพัทธ์ เป็น สี่เหลี่ยม
ตีความ แผนภาพเวนน์ ออยเลอร์ แบบต่าง ๆ
ไอเดียคือต้องมองให้ออกว่า แต่ละบริเวณมีความหมายว่าอย่างไร
บทความนี้ พี่จะยังไม่เข้าลึกไปถึงการเขียน แผนภาพเวนน์ ออยเลอร์ กับ ตัวดำเนินการทางเซต \(\;\cap\;,\;\cup\;,\;-\;,\;^{\prime}\) จะรวมให้ไว้ทีเดียวในบทนั้นเลย ส่วนบทความนี้ เราจะเน้นการมองแผนภาพเวนน์ ให้ออกว่า ถ้ามีเซต \(A,B,C,\dots\) เราสามารถนำทุกเซตมาเขียนในแผนภาพเวนน์ 1 ภาพ ได้ยังไงกันบ้าง
แบบที่ 1 กรณีมี 1 เซต
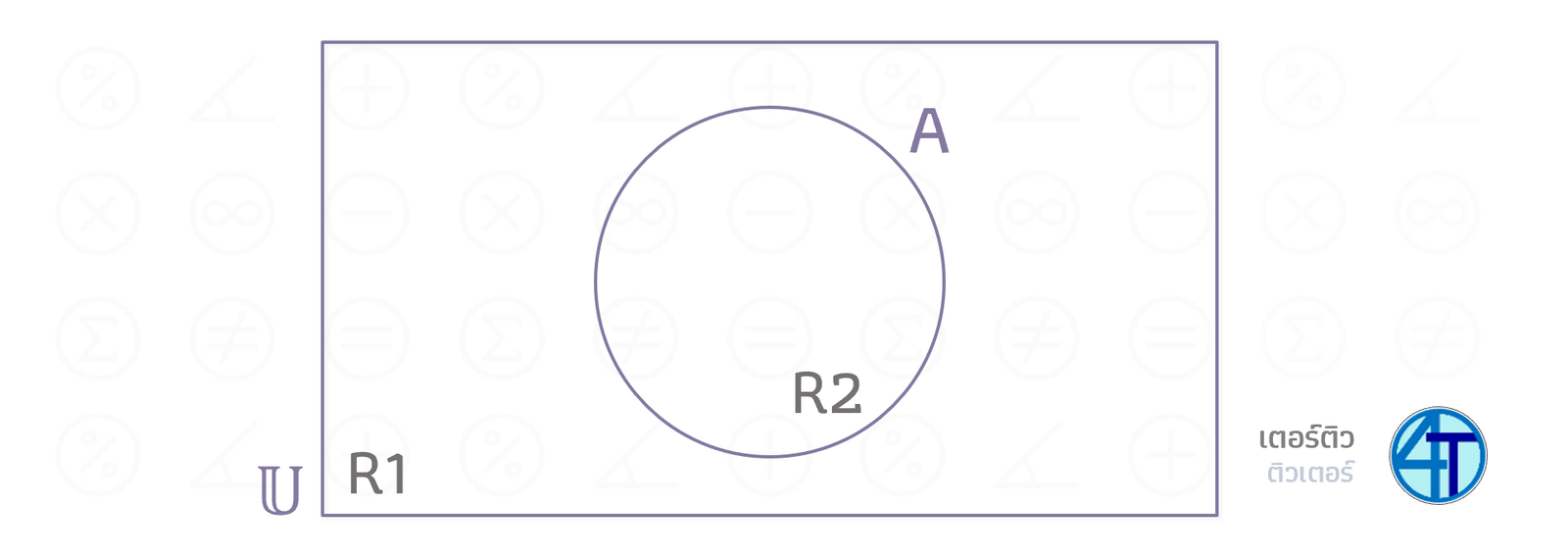
กรณีนี้ก็จะเหมือนในตัวอย่างด้านบนเลย ต่อไปนี้พี่จะขอแทนว่า Region (ย่อด้วยตัว R) มาจากคำว่า บริเวณ คล้าย ๆ กับการแบ่งเขตจังหวัดอะไรประมาณนั้น หากน้องสังเกตรูปด้านบน เราจะเห็นว่ามันมีทั้งหมด 2 Regions ด้วยกัน ได้แก่ R1 และ R2
การตีความหมายของ แผนภาพเวนน์ ออยเลอร์ ก็ไม่ยากเลยครับ ส่วนไหนอยู่ในเซตไหนก็แสดงว่ามันเป็นสมาชิกของเซตนั้น นั่นเอง ลองสังเกตแยกพื้นที่กันดูนะ
พื้นที่ R2 มันอยู่ในวงกลม \(A\) และก็อยู่ในสี่เหลี่ยม \(\mathbb{U}\) ด้วยถูกมั้ยเอ่ย แสดงว่าพื้นที่ R2 นี้คือสมาชิกทั้งหมดที่ อยู่ใน \(A\) และก็อยู่ใน \(\mathbb{U}\) ด้วย (ซึ่งอันนี้มันก็แน่นอนอยู่แล้ว เพราะสมาชิกทุกตัวต้องอยู่ในเอกภพสัมพัทธ์ หรือ ขอบเขตที่เราสนใจนั่นเอง ดังนั้น จากนี้ไปเราจะไม่พูดถึง \(\mathbb{U}\) อีก)
พื้นที่ R1 มันไม่อยู่ในวงกลม \(A\) แปลว่าเป็นสมาชิกทั้งหมดที่ ไม่ได้อยู่ ใน \(A\) นั่นเอง
แบบที่ 2 กรณีมี 2 เซต
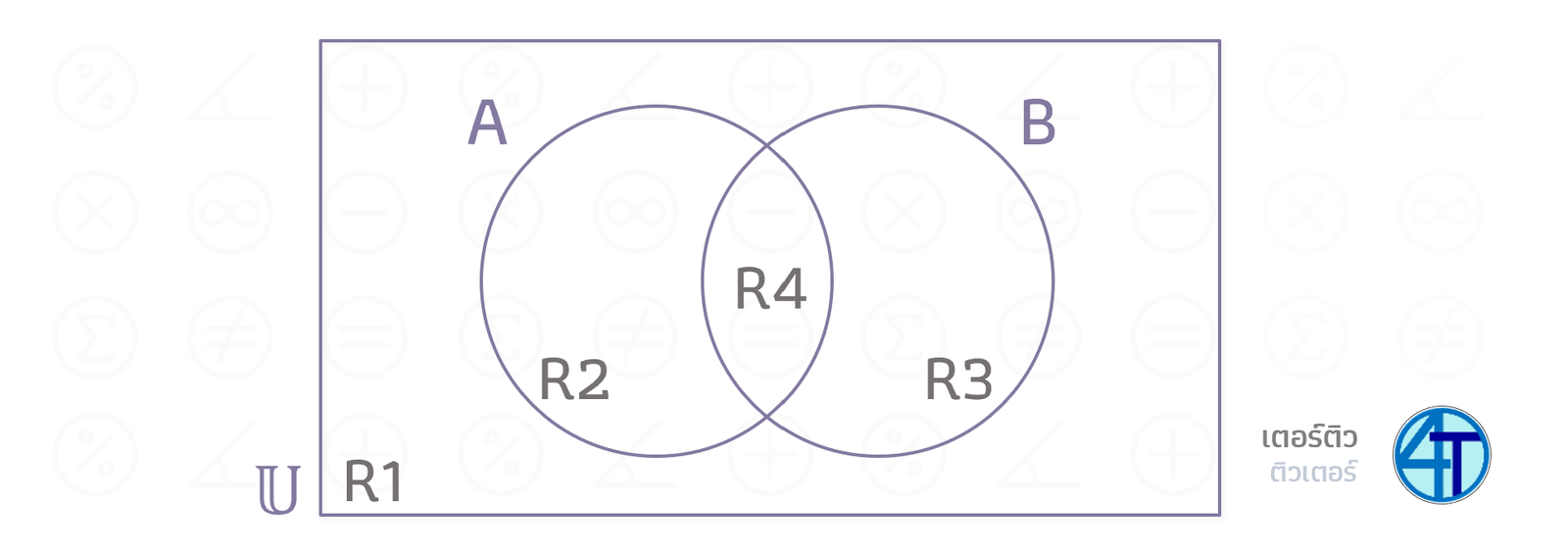
พื้นที่ R1 ไม่อยู่ในวงกลมไหนเลย แสดงว่าเป็นสมาชิกที่อยู่ในขอบเขตที่สนใจ (\(\in \mathbb{U}\)) แต่ \(\notin A\) และ \(\notin B\)
พื้นที่ R2 อยู่ในวงกลม A แค่อันเดียว ไม่ได้อยู่ในวงกลม B แปลว่า \(\in A\) แต่ \(\notin B\)
พื้นที่ R3 อยู่ในวงกลม B แค่อันเดียว ไม่ได้อยู่ในวงกลม A แปลว่า \(\notin A\) แต่ \(\in B\)
พื้นที่ R4 อยู่ในวงกลมทั้งคู่ แสดงว่า \(\in A\) และ \(\in B\)
แถม ถ้าถามว่าทำไมรูปถึงเป็นแบบนี้ ทำไมสองวงกลมถึงต้องมีส่วนที่ทับซ้อนกัน ลองคิดตามดูนะถ้าพี่มี \(3\in A\) และ \(3\in B\) ด้วย หากพี่เขียนวงกลมแยกกัน พี่จะเอา \(3\) ไปไว้ส่วนไหนถูกม้ะ เพราะเราแยกร่าง \(3\) ไม่ได้ เลข \(3\) มันต้องไปอยู่ Region ที่อยู่ทั้งในวงกลม \(A\) และก็ \(B\) ด้วย ดังนั้นมันก็คือ R4 ตามภาพข้างบนนั่นเอง ถ้าไม่มี R4 เราก็จะไม่มีทางนำ \(3\) ไปใส่ให้อยู่ในทั้งสองวงกลมได้
แบบที่ 3 กรณีมี 3 เซต
อันนี้คือแบบสุดท้าย ถ้า > 3 ส่วนมากจะไม่นิยมเขียนแผนภาพเวนน์ เนื่องจากพื้นที่ทับซ้อนจะมองเป็นภาพยากมาก
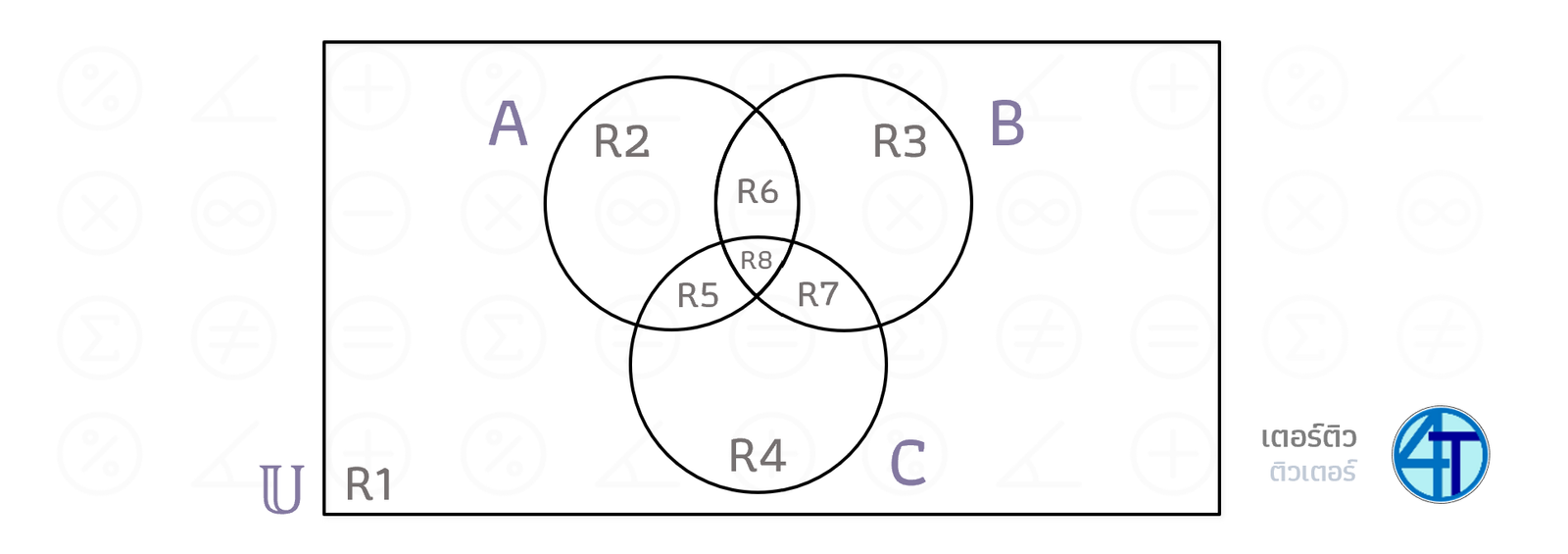
ไม่รู้ว่าน้องๆ ยุคนี้คุ้นเคยกันตราแบบนี้หรือเปล่า มันคือตราเดียวกันกับช่อง 7 สีเลย (สมัยนี้ช่องทีวีดิจิตอลเยอะเกิน แต่ก่อนมันมีให้ดูแค่ 6 ช่องอะ คือยังไงก็ต้องมีเปิดมาช่อง 7 บ้าง) สังเกตว่าเราจะมีทั้งหมด 7 Regions ถ้าไม่รวม R1 ที่อยู่ข้างนอกทุกวงกลม
พื้นที่ R1 เหมือนเดิมไม่อยู่ในวงกลมไหนเลย \(\notin A,\notin B, \notin C\)
พื้นที่ R2 \(\in A, \notin B, \notin C\)
พื้นที่ R3 \(\in B, \notin A, \notin C\)
พื้นที่ R4 \(\in C, \notin A, \notin C\)
พื้นที่ R5 ลองมองดีๆ น้องจะเห็นว่า R5 อยู่ในวงกลม A และ C แต่ไม่อยู่ใน B ดังนั้น \(\in A, \in C, \notin B\)
ลองทำ R6, R7, R8 เองนะ
แผนภาพเวนน์ ออยเลอร์ แบบมีเงื่อนไข
ไม่จำเป็นว่ารูปแบบการทับซ้อนต้องเหมือนกับที่แสดงให้ดูในหัวข้อที่แล้วเสมอไป
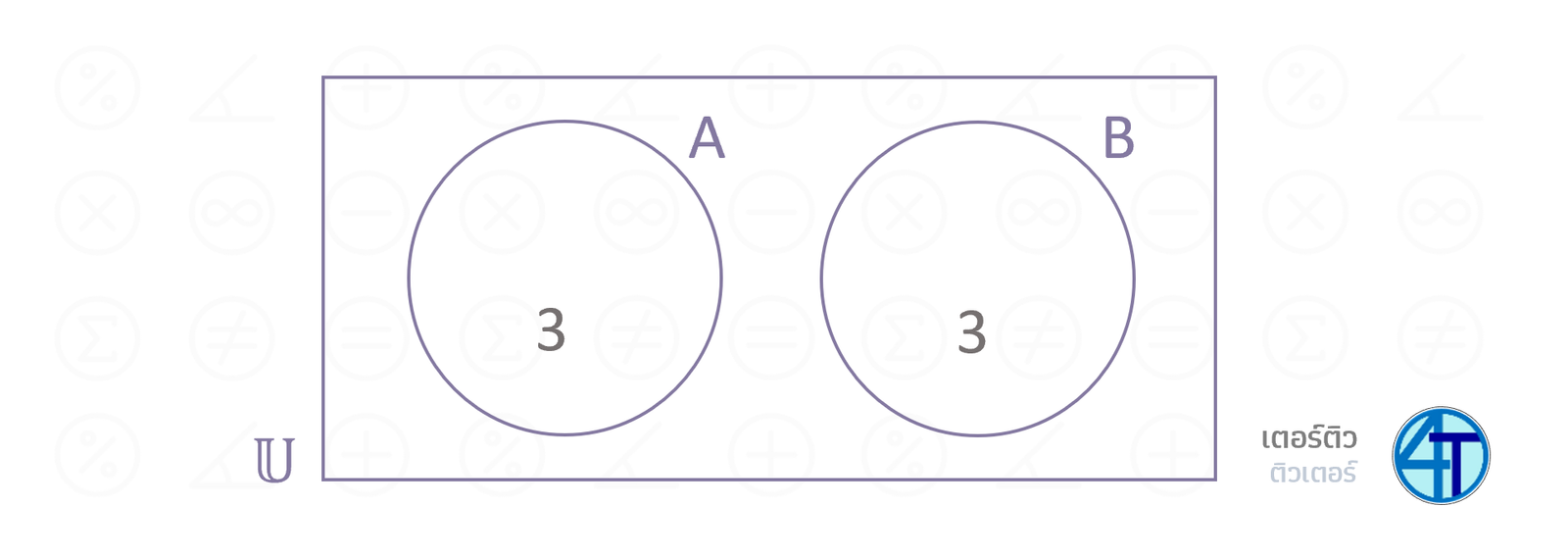
ภาพด้านล่างนี้คือการที่ เซต \(A\) และ \(B\) ไม่มีสมาชิกร่วม กันเลยนั่นเอง จำที่เคยบอกไปข้างบนได้กันไหมเอ่ย ว่าถ้าสองเซตนี้มันมีสมาชิกร่วม เราต้องเขียนมันทับซ้อนกัน เพื่อที่จะสร้าง Region ใหม่ (R4 ในตัวอย่างข้างบน) เพื่อให้เป็น Region ที่อยู่ทั้งใน \(A\) และ \(B\) แต่ถ้าเขียนแยกแบบนี้แสดงว่าสองเซตนี้ไม่มีสมาชิกร่วมกันนั่นเอง

ไม่มีสมาชิกร่วม
ด้านล่างอันนี้ก็ไม่ยาก สังเกตมั้ยว่า วงกลม \(A\) อยู่ข้างในวงกลม \(B\) ทั้งหมดเลย มันหมายความว่า สมาชิกในวงกลม \(A\) (\(\in A\)) ก็อยู่ในวงกลม \(B\) ด้วย (\(\in B\)) แปลว่า สมาชิกทุกตัวของ \(A\) เป็นสมาชิกของ \(B\) ด้วยเช่นกัน คุ้นๆ ประโยคนี้กันหรือเปล่าเอ่ย ใช่แล้ว! มันคือประโยคในเรื่อง สับเซต งั้นก็แปลว่า \(A\subset B\)
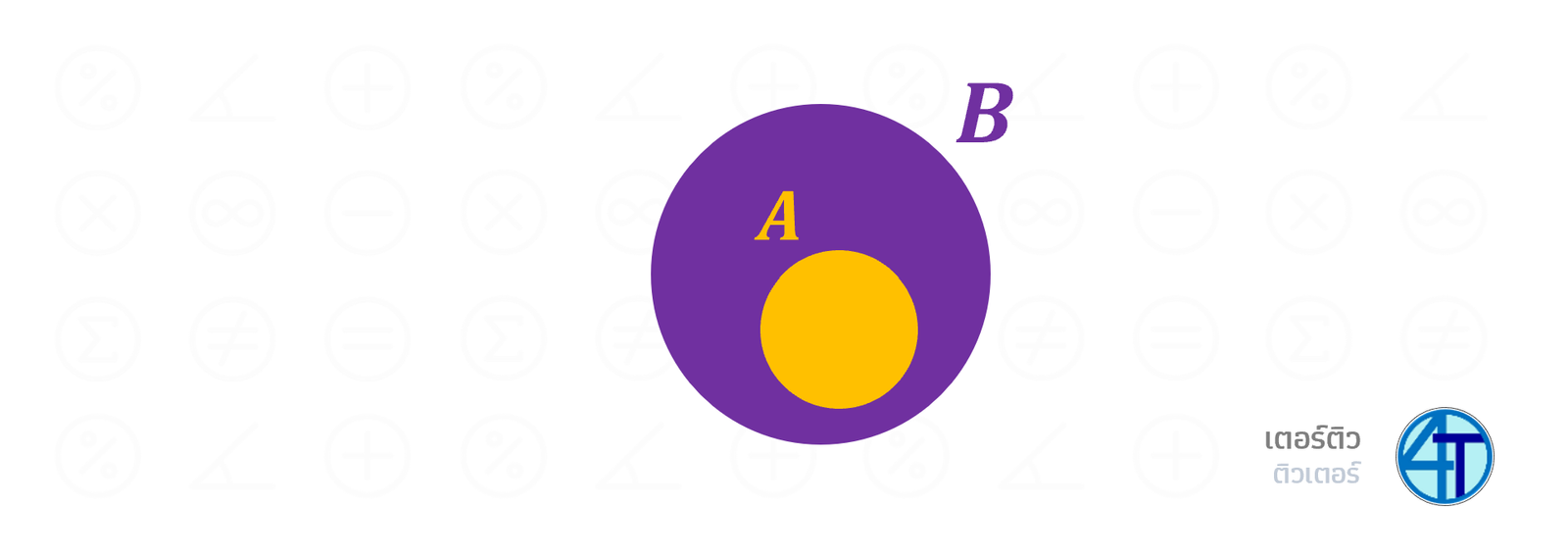
สับเซต
หากบทความพี่เป็นประโยชน์ ฝากแชร์ต่อให้เพื่อนๆ ด้วยนะครับ :')
