สับเซต ม.4 \(\subset\)

สับเซต คืออะไร

สับเซต (subset) อธิบายง่ายๆ มันก็มีความหมายเหมือนรากศัพท์ (sub-) เลยครับน้อง ๆ sub- แปลว่า ภายใต้ อะไรประมาณนี้ ดังนั้นคำว่า สับเซต ก็คือ เซตที่เป็นเซตย่อยภายใต้เซตใด ๆ นั่นเอง ส่วน สัญลักษณ์ที่ใช้ก็คือ \(\subset\) คล้ายๆ เกือกม้าตะแคง

อันนี้ขอนอกเรื่อง ใครเวลาว่างก็อ่านเล่นได้ 55555+ เห็นคำว่า “สับ” ใช่ไหมครับน้องๆ ในเรื่องนี้ เราจำมันง่าย ๆ เหมือนสับหมูบนเขียงก็ได้ ถ้าเราหยิบหมูมาหนึ่งก้อนใหญ่ แล้วเราเอามีดมาสับ มันเป็น ยังไงเอ่ย ใช่แล้ว มันก็จะเล็กลงถูกไหมครับ แต่มันก็ยังเป็นหมูชิ้นเดิม แค่เราสับมันออกมาแค่บางส่วน เรื่องเซตนี้ก็เหมือนกัน สมมุติพี่มีเซต \(A = \{1, 2, 3, 9, 13\}\) พี่เอามาวางบนเขียงแล้วสับ

เราก็จะได้สองเซต เซตแรก (ด้านซ้าย) \(B = \{1, 2, 3\}\) และเซตที่สอง (ด้านขวา) \(C = \{9, 13\}\) ซึ่งทั้ง \(B \subset A\) และ \(C \subset A\) นั่นเอง

ดังนั้น สรุปได้สั้น ๆ ว่า เซต S ใด ๆ จะเป็นสับเซตของเซต T ใด ๆ ได้ก็ต่อเมื่อ ทุกๆ สมาชิกของ S นั้นเป็นสมาชิกของ T ด้วยเช่นกัน สังเกตกันหรือเปล่าครับว่าการที่เรานำเซตใหญ่มา “สับ” ออกมันก็เหมือนกับการที่เราได้เซตที่เล็กลง แต่ สมาชิกของเซตก็ยังคงเป็นสมาชิกที่เรานำมาจากเซตใหญ่นั่นเอง

ดังนั้น สมาชิกทุกตัวในสับเซตก็เลยเป็นสมาชิกในเซตใหญ่ด้วย

ข้อควรจำเกี่ยวกับสับเซต (สมบัติของสับเซต)

ข้อสังเกต ตามนิยามในกรอบข้างบนนั้น เราถือว่าเซตทุกตัวเป็นสับเซตของตัวมันเอง นั่นก็คือ \(A \subset A\) เพราะสมาชิกทุกตัวใน \(A\) ก็ต้องอยู่ใน \(A\) และเราถือว่าเซตว่างเป็นสับเซตของทุกเซต \(\varnothing \subset A\) เมื่อ \(A\) เป็นเซตใด ๆ ก็ตาม

มองภาพง่ายๆ กันแบบนี้ก็ได้ เมื่อกี้พี่ “สับ” เซตถ้าพี่เลื่อนตำแหน่งกรรไกรมาตรงนี้หล่ะ

พี่ถามว่าด้านซ้ายของกรรไกรมีอะไร ก็มีหมูชิ้นเดิมที่ไม่ได้ถูกตัดใช่ไหมครับ และด้านขวาหล่ะ ก็ไม่มีอะไรเลย (ว่างเปล่า)

ดังนั้น มันเลยเป็นที่มาที่ว่า \(A \subset A\) และ \(\varnothing \subset A\) นั่นเอง

สับเซตแท้ คืออะไร

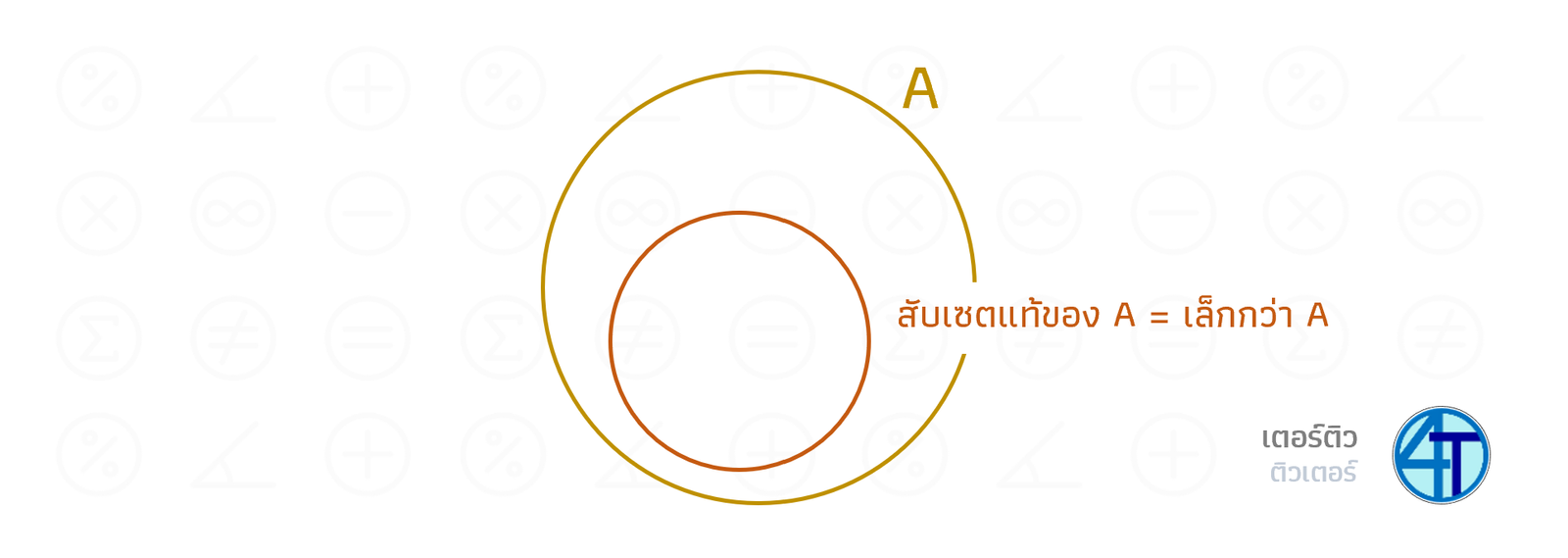
ไหนลองเดากันจากคำพูด “สับเซตแท้” กันดูสิ ว่ามันคืออะไร มันก็คือ สับเซตที่แท้จริง นั่นเองน้อง ๆ บางคนยังมองไม่เห็นภาพว่า พี่คำว่าแท้จริง นี่มันหมายความว่ายังไง คำว่า แท้จริง ก็คือ มันเป็นสับเซต (เซตย่อย) จริง ๆ นะ ซึ่งมันก็หมายความว่า สับเซตแท้เนี่ย มันควรจะมีขนาด เล็กกว่า เซตตั้งต้นนั่นเองครับ

ดังนั้น เราเรียกสับเซตทุกอันของเซต \(A\) ใด ๆ ที่ไม่ใช่ตัวมันเองว่า “สับเซตแท้” (\(A\) เป็นสับเซตของ \(A\) แต่ไม่ใช่สับเซตแท้ของ \(A\))

การเขียนแจกแจงสับเซตทั้งหมดของเซตใดๆ แบบมีหลักการ ไม่ลืมตัวไหนแน่นอน

คราวนี้เราลองมาดูว่าสมมุติเรามีเซต \(A\) ใด ๆ มา เราจะแจกแจงเขียนสับเซตของมันออกมาได้ทุกตัวอย่างไรได้บ้าง สมมติ เรากำหนดให้ \(A = \{1, 2, 3\}\) ให้เรามองแบบนี้ สมาชิกในเซต \(A\) มีกี่ตัว \(n(A)\) = 3 ใครลืมวิธี การนับสมาชิก กลับไปดูบทก่อน ๆ ด่วนเลย

เพราะฉะนั้นเราจะไล่เขียนสับเซตเริ่ม ตั้งแต่สับเซตที่มีสมาชิก 0 ตัวไปต่อที่ 1 ตัว ไปเรื่อยๆ จนถึง 3 ตัว

0 ตัว : \(\{\;\}\)
สมาชิกศูนย์ตัว คือเซตว่าง (เป็นที่มาว่าทำไมเซตว่างเป็นสับเซตของทุกเซต)

1 ตัว : \(\{1\}, \{2\}, \{3\}\)
สมาชิกหนึ่งตัว เราก็ดูว่าถ้าหยิบมา 1 ตัวจาก A มีกรณีไหนเป็นไปได้บ้าง

2 ตัว : \(\{1, 2\}, \{1, 3\}, \{2, 3\}\)
สมาชิกสองตัว เราก็ดูว่าถ้าหยิบมา 2 ตัวจาก A มีกรณีไหนเป็นไปได้บ้าง

3 ตัว : \(\{1, 2, 3\}\)
สมาชิกสามตัว เราก็ดูว่าถ้าหยิบมา 3 ตัวจาก A มีกรณีไหนเป็นไปได้บ้าง

การเช็คว่าเป็นสับเซตหรือไม่

คือพี่ไม่ได้บอกโดยละเอียดในหัวข้อก่อน ๆ ว่าการดูว่าเซตใด ๆ เป็นสับเซตของเซตใด ๆ ทำอย่างไร หัวข้อนี้เลยขออนุญาตแถมสั้น ๆ ว่าจะเช็คได้ยังไงบ้าง ก่อนอื่นจำนิยามสับเซตกันได้หรือเปล่าเอ่ย

คีย์เวิร์ดที่พี่อยากเน้นคือ ทุกๆ สมาชิก ตรงนี้แหละน้อง การเช็คสมาชิก สมมติต้องการเช็คว่า \(B \subset A\) หรือเปล่า เราก็ ไล่ทุกสมาชิกใน \(B\) แล้วนำไปดูว่ามีอยู่ใน \(A\) หรือเปล่า

• หากมีตัวไหนไม่อยู่ แสดงว่า \(B \not\subset A\)
• แต่หากอยู่หมดก็แสดงว่า \(B \subset A\)

ตัวอย่างเช่นหากเรามี \(B=\{4,5,6\}\) และ \(A=\{1,2,4,6\}\) ถ้าเราอยากเช็คว่า \(B\stackrel{?}{\subset} A\) เราจะไล่ทุกสมาชิกใน \(B\) นั่นก็คือ \(4\), \(5\) และ \(6\) เพื่อดูว่าทุกตัวอยู่ใน \(A\) หรือไม่ ซึ่งจะเห็นได้ว่า \(5\notin A\) ดังนั้น \(B\not\subset A\)

แบบฝึกสมอง

แต่ละข้อจงหาว่า \(A\) เป็นสับเซตของ \(B\) หรือไม่