การหาจำนวนสมาชิกของเซต ม.4

การหาจำนวนสมาชิกในเซต (ทั่วไป)

อย่างที่พี่ได้กล่าวไปแล้วในหัวข้อ เซตจำกัดกับเซตอนันต์ เรารู้กันอยู่แล้วถูกไหมครับ ว่าเซตอนันต์มีจำนวนไม่จำกัดหรือที่ เราเรียนกันว่า อินฟินิตี้ (\(\infty\)) กันนั่นแหละครับ เพราะฉะนั้นในหัวข้อนี้เราจะไม่สนใจมัน เพราะนับไปก็ไม่ได้อะไร เนื่องจากมันเป็นค่าอนันต์ (มากมายเหลือเกินจนนับไม่ได้) เราจะสนใจแต่ เซตจำกัด (finite set)

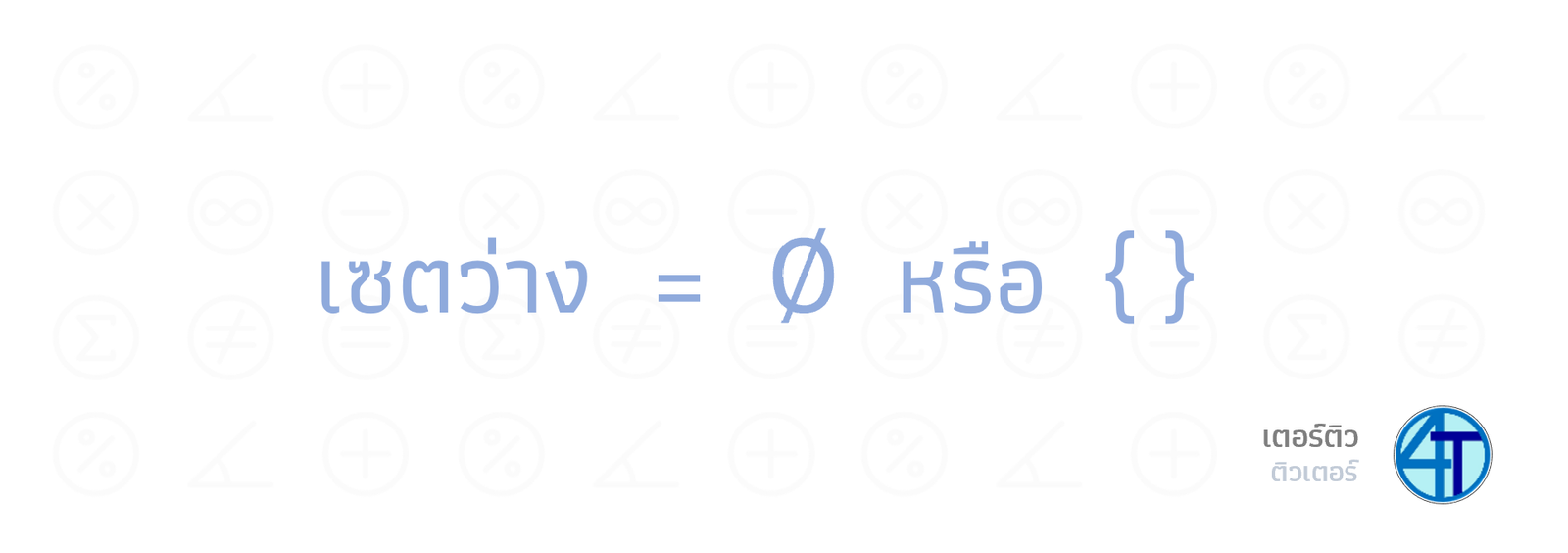
ก่อนอื่นเรามาแนะนำสมาชิกตัวใหม่ในบ้านเราก่อน นั่นก็คือ เซตที่มีจำนวนสมาชิก 0 ตัว อย่าพึ่งงงไปกันครับน้อง เซตนี้ หน้าตาอย่างที่เราคิดกันไว้นั่นแหละครับ มันคือ \(\{\;\}\) แค่ปีกกาแต่ไม่มีอะไรข้างในเลยแม้แต่ตัวเดียว เราเรียกเซต \(\{\;\}\) ว่า เซตว่างซึ่งมีสัญลักษณ์การเขียนเซตว่างอีกรูปแบบหนึ่งคือ \(\varnothing\)

การถามหาจำนวนสมาชิกในเซตนั้นเราใช้ตัว \(n\) เป็นสัญลักษณ์อย่างเช่น \(n(A)\) คือ จำนวนสมาชิกในเซต \(A\) ดังนั้นกลับไปดู ในย่อหน้าที่แล้วกัน \(n(\{\;\})\) หรือ \(n(\varnothing)\) ก็จะเท่ากับ ศูนย์ นั่นเอง เนื่องจากมันไม่มีสมาชิก หรือก็คือมี สมาชิกทั้งหมดศูนย์ตัว \(n(\varnothing) = 0\)

อีกตัวอย่าง หากเรากำหนดให้เซต \(A= \{1, 2, 3, 4, 7, 7\}\) ถามว่ามีจำนวนสมาชิกหรือ \(n(A)\) เนี่ยมีค่าเท่าไหร่ครับ เหมือนจะได้ยินอยู่ 2 คำตอบ บางคนตอบ 6 บางคนก็ตอบ 5 งั้นเรามาดูกันเลยดีกว่า สำหรับ คนที่ตอบ 6 ตัว ก็จะบอกพี่ว่าก็มันมี เลข \(1, 2, 3, 4, 7\) และก็ \(7\) ไงพี่ รวมเป็น 6 ตัว คำตอบนี้ผิด ยังจำ คุณสมบัติเซต กันได้หรือเปล่าครับ ที่บอกว่า เซตไม่นับซ้ำ ในที่นี้เลข 7 ซ้ำเราก็จะไม่สนใจมันและลดตัดทอนมันเหลือแค่ตัว เดียวพอ \(A\) จึงเขียนใหม่ได้เป็น \(\{1, 2, 3, 4, 7\}\) ซึ่ง \(n(A)=5\) นั่นเอง

"ง่ายจังพี่ แล้วแบบที่ยากคือยังไงครับ" ถ้ามันง่ายขนาดนี้เด็กคงทำกันได้ทั้งประเทศและแหละ ใช่ม้ะน้อง อยากรู้ว่าแบบยากนี่คือยังไง เลื่อนไปหัวข้อต่อไปกันเลย

การหาจำนวนสมาชิกในเซตแบบยาก (เซตแจกแจงสมาชิก)

ลองดูตัวอย่างดังต่อไปนี้ครับ \(A=\{1, \{\}, \{2\}, \{\{3\}, 1\}\}\) เซตนี้เป็นแบบแจกแจงสมาชิกถูกไหมเอ่ย ไม่ใช่บอกเงื่อนไขนะ ใครแยกไม่ออกรีบกลับไปดู เนื้อหาพื้นฐาน ก่อนเลย 55555+

เธอเห็นวงเล็บนั่นไหม เยอะเสียเหลือเกิน เห็นยังน้อง ว่ามันมีความยากขึ้นมาอีกเสต็ปอย่างเห็นได้ชัดเลย แล้วทีนี้ถ้าเจอโจทย์แบบนี้หละ เรามีหลักการยังไงในการแก้

หลักการของเราคือ มองคู่วงเล็บให้ออกว่าวงเล็บไหนคู่วงเล็บไหน เพราะคู่วงเล็บ 1 คู่ = 1 เซต เดี๋ยวพี่จะทำสีให้น้องมองให้ง่ายขึ้น

พอเห็นสีกันแล้ว สังเกตกันหรือเปล่าว่ามีทั้งหมด 5 เซตด้วยกัน ในโจทย์ข้อนี้ (เพราะมี 5 สี: แดง ฟ้า เขียว ม่วง ส้ม) โจทย์จะถามเราว่า \(n(A)\) เท่ากับเท่าไหร่ แปลว่า "จำนวนสมาชิกในเซต \(A\)" ซึ่งก็คือเซต สีแดง ที่คลุมทุกอย่างอยู่ มีสมาชิกทั้งหมดกี่ตัวนั่นเอง

หลักการนะน้อง คือ การเขียนเซตเนี่ย เราจะใช้เครื่องหมายจุลภาค (,) ในการคั่นระหว่างตัวสมาชิก ดังนั้น เราจะดูตัวคั่นนี่แหละเพื่อหาคำตอบ แต่อย่าพึ่งรีบดีใจไปว่า แค่นับแล้วจบ น้องลองนับตามในภาพข้างบนดูครับ สังเกตว่า มี , อยู่ทั้งหมด 4 อันแปลว่า จำนวนสมาชิกคือ 5 อย่างนั้นหรอ? (การที่มี , คั่น 2 อัน แสดงว่ามี 3 สมาชิก \(\{1, 2, 3\}\) การที่มี , คั่น 3 อัน แสดงว่ามี 4 สมาชิก \(\{1, 2, 3, 4\}\) โดยปกติ)

คำตอบคือไม่ใช่ 5 ตัว เพราะเราไม่สามารถนับ เครื่องหมาย , ทั้งหมดและนำมาตอบได้ เพราะอะไร ลองสังเกต เซตสีม่วง \(\{\{3\},1\}\) สังเกตว่า เครื่องหมายจุลภาคที่กั้นนั้นมันกั้นสมาชิกใน เซตสีม่วง แต่ไม่ได้กั้นสมาชิกในเซตสีแดง (เซต \(A\)) แสดงว่า จุลภาค อันนี้ ไม่ควรเอามานับด้วย เพราะฉะนั้น น้องต้องมองให้ออกว่า จุลภาคอันไหนบ้างที่กั้นสมาชิก ของเซต \(A\) อยู่นั่นเอง

แสดงว่าหลักการการหาจำนวนสมาชิกคือ (1) จับคู่วงเล็บให้ได้ (2) นับแค่เครื่องหมาย , ที่กั้นสมาชิกของเซตใหญ่ (ในตัวอย่างคือเซต \(A\)) ของเรา เมื่อได้มาแล้ว ก็จับไปบวก 1 (จุลภาค \(n\) ตัวคั่นได้ \(n+1\) สมาชิก) ส่วนคำถามต่อไปคือ แล้วเราจะจับคู่วงเล็บได้ยังไง สำหรับคนที่ไม่เคยทำมาก่อน

หลักการคือ นำวงเล็บนอกสุดออกไปก่อน (ในตัวอย่างคือวงเล็บสีแดง) แล้วไล่จากซ้ายไปขวา และใช้วิธีการ +1 -1 เมื่อเราเจอ วงเล็บเปิดให้ +1 ส่วนวงเล็บปิดให้ -1 แล้วถ้ามันเป็นศูนย์เมื่อไหร่แสดงว่าเจอคู่ แนะนำให้ดูวิดีโอด้านบนเพิ่มเติมสำหรับรายละเอียดและตัวอย่างการหาคู่วงเล็บครับ

ข้อควรระวัง

• อย่าลืมว่าเซตเราไม่นับตัวซ้ำ เพราะฉะนั้นอย่าลืมเช็คด้วยว่า มีสมาชิกไหนซ้ำกันหรือไม่ หากซ้ำให้ตัดออกเหลือเพียงตัวเดียว
• เซตว่างเขียนได้สองแบบ \(\{\;\}\) หรือ \(\varnothing\) ดังนั้นหากเจอทั้งคู่ แสดงว่าเป็นสมาชิกตัวเดียวกัน ตัดออกได้
• แต่! \(\{\}\) กับ \(\{\{\}\}\) ไม่ใช่ตัวเดียวกัน \(\{\}\) คือเซตว่าง มีสมาชิก 0 ตัว แต่ \(\{\{\}\}\) คือ เซตที่มีเซตว่างอยู่ข้างใน เป็นสมาชิกอีกที ดังนั้น \(\{\{\}\}\) มีสมาชิก 1 ตัวคือ เซตว่าง

การหาจำนวนสมาชิกในเซตแบบยาก (เซตบอกเงื่อนไข)

การเขียนเซตแบบบอกเงื่อนไขนี่เจอบ่อยมากในข้อสอบ เพราะว่าโจทย์มัน พลิกแพลงได้เยอะมากๆ เพราะอะไร เพราะเงื่อนไขสามารถเป็นอะไรก็ได้ เช่น \(A=\{x\in I\,|\,|2x-9|\leq 11\}\) ( โจทย์ PAT1 ตุลา 55 ) สังเกตไหมเอ่ยว่า การหาว่ามีสมาชิกกี่ตัวใน \(A\) นั้น ไม่ค่อยจะเกี่ยวกับเซตมากเท่าไหร่เลย มันคือการแก้อสมการซะมากกว่าด้วยซ้ำไป

ใช่แล้วน้องเรื่องการหาจำนวนสมาชิกของเซตแบบบอกเงื่อนไขนั้น ส่วนมากจะใช้ความรู้คณิตฯ ในบทอื่นๆ มาแก้เสียมากกว่า น้องต้องหาให้ได้ว่า มีสมาชิกเป็นใครบ้างตามเงื่อนไขที่โจทย์บอกมา เช่น หากโจทย์ให้ \(B=\{x\,|\,x^2=25\}\) น้องก็ต้องแก้สมการและจะทราบว่า \(5^2=25\) และก็ \(-5^2=25\) แสดงว่า \(B=\{5,-5\}\) ดังนั้น สมาชิกก็มีสองตัวนั่นเองครับ

เพราะฉะนั้น ในส่วนนี้ เราก็จำแค่คอนเซปต์เรื่องเซตไปก่อน และอนาคตโจทย์การหาว่ามีสมาชิกอะไรในเซตบ้าง เราจะใช้เนื้อหาบทอื่นมาช่วยแก้ปัญหากัน

สูตรจำนวนสมาชิกของเซต (แถม)

อันนี้พี่บอกว่าแถมเพราะหากน้องยังเรียนไม่ถึงบท ตัวดำเนินการของเซต สามารถไปทำความเข้าใจก่อนและค่อยกลับมาอ่านตรงนี้นะ

• \(n(A\cup B)=n(A)+n(B)\)\(\,-\,n(A\cap B)\)
• \(n(A\cup B\cup C)\)\(\,=n(A)+n(B)+n(C)\)\(\,-\,n(A\cap B)-n(A\cap C)\)\(\,-\,n(B\cap C)+n(A\cap B\cap C)\)

ที่มาของสูตรอันนี้ก็ไม่ยาก ให้น้องลองนึกถึง แผนภาพเวนน์ฯ จะมองเห็นภาพง่ายมากขึ้น หลักการมันคือ

อย่างเช่น \(n(A\cup B\cup C)\) เริ่มจาก บวกทีละ 1 ตัวก่อน \(+n(A)+n(B)+n(C)\) จากนั้น ลบทีละ 2 ตัว \(-n(A\cap B)-n(A\cap C)-n(B\cap C)\) และก็ บวกทีละ 3 ตัว \(+n(A\cap B\cap C)\)

แบบฝึกสมอง

จงหาจำนวนสมาชิกของเซตต่อไปนี้ (เรียงง่ายไปยาก)