เลือกอ่านตามหัวข้อ?
เข้าหาบทความพี่ง่ายๆ จาก Google


กฎของไซน์ (The Law of Sines)
เดินทางมาถึงเรื่องสุดท้ายท้ายสุดในตรีโกณมิติ ม.5 ซึ่ง เป็นเรื่องที่สูตรไม่เยอะ และค่อนข้างง่าย ดังนั้นไปเริ่มกันเลยครับ
กฎของไซน์กับกฎของโคไซน์นั้นให้น้องจำไว้เลยว่า เกี่ยวกับสามเหลี่ยม ซึ่งใน ม.3 เราเรียนเรื่องสามเหลี่ยมมุมฉาก กันไปแล้วในตรีโกณมิติ ม.3 พอมา ม.5 ก็ไม่ได้เซอร์ไพร์สอะไรมาก โดยเราจะใช้ กฎของไซน์และโคไซน์ กับ สามเหลี่ยมใด ๆ (แปลว่าไม่ต้องเป็นมุมฉากก็ใช้ได้นะ)
รูปสามเหลี่ยมในกฎของไซน์และกฎของโคไซน์ ตามมาตรฐานเลยจะเป็นดังรูปด้านล่างนี้ คือ สามเหลี่ยม \(ABC\) โดยที่ด้านตรงข้ามมุมไหนก็จะใช้ความยาวด้านเป็นอักษรนั้น (แต่ใช้ตัวพิมพ์เล็ก) เช่น ตรงข้ามมุม \(A\) คือ ด้านที่ความยาว \(a\) เป็นต้น
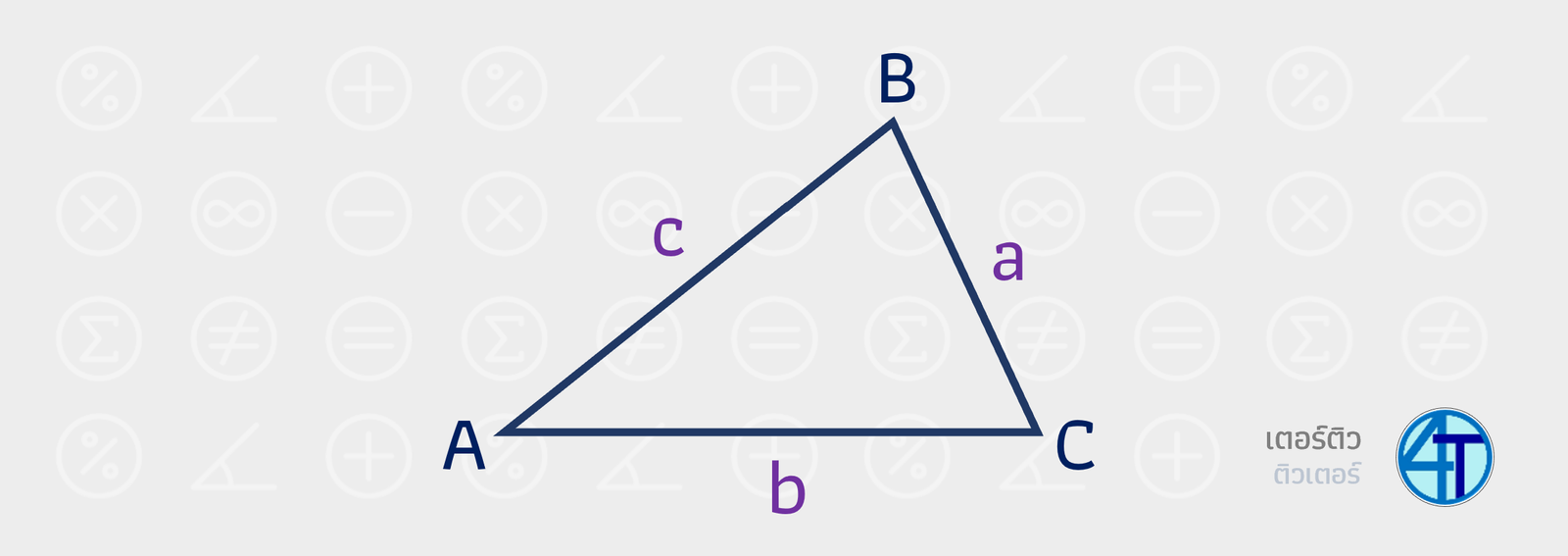
\(\dfrac{\sin{A}}{a}=\dfrac{\sin{B}}{b}=\dfrac{\sin{C}}{c}\)
กฎของโคไซน์ (The Law of Cosines)
เรื่องนี้ให้น้องนึกถึงสามเหลี่ยมพีทาโกรัสที่เราเคยเรียนตอน ม.2 พี่ขอเรียกมันว่า พีทาโกรัสแอดวานซ์ และกัน เพราะสูตรมันล้อกันมาเลย แต่ใน พีทาโกรัสเราเรียนกันว่า มันจะเวิร์คก็ต่อเมื่อเป็น สามเหลี่ยมมุมฉาก
ดังนั้น พี่ว่าน้องพอจะเดาออกกันและ กฎของโคไซน์คือสูตรที่ใช้ได้กับ สามเหลี่ยมทุกรูปแบบ ไม่ว่าจะมุมไหน ใด ๆ ก็ตาม ด้านล่างคือสูตรพีทาโกรัสตอน ม.2
\(c^2=a^2+b^2\)
ให้น้องสังเกตรูปสองอันนี้ให้ดี ๆ และสูตรมันจะเหมือนเดิมแค่เพิ่มพจน์ท้ายมา ดังนี้
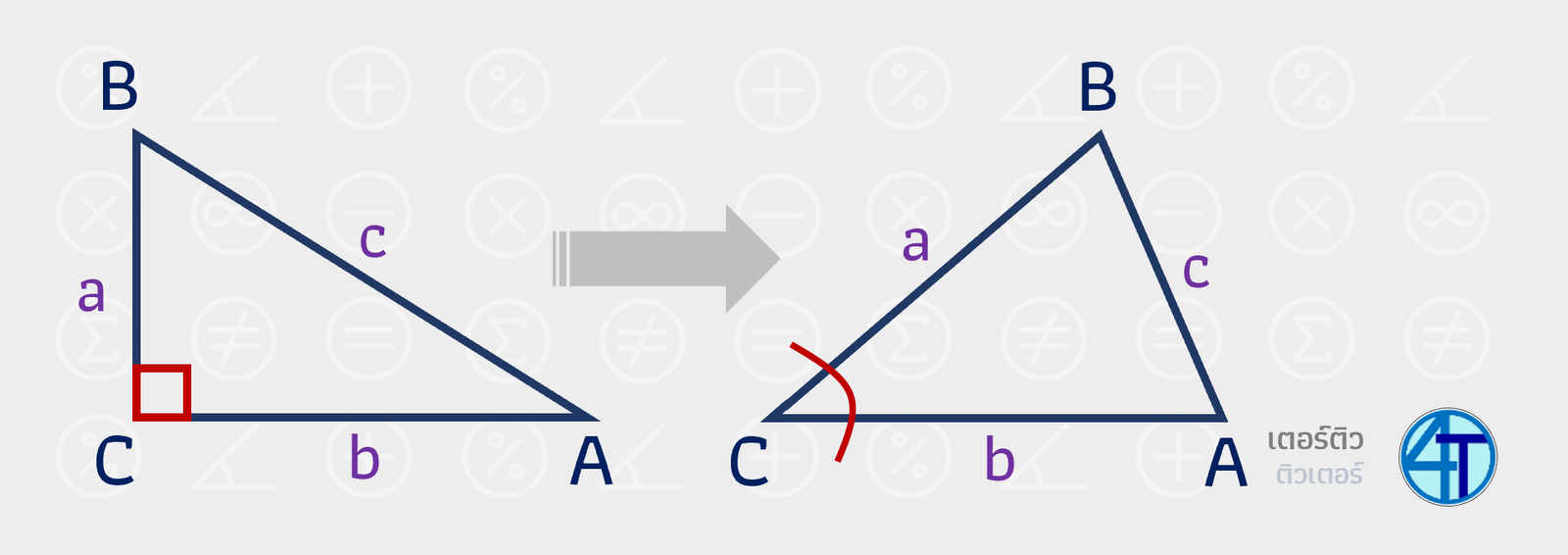
\(c^2=a^2+b^2\textcolor{blue}{-2ab\cos{C}}\)
จุดที่แตกต่างกันก็คือ มุม C มุมระหว่างด้านประกอบ \(a\) กับ \(b\) ที่เรานำมาคิดจะมีส่วนเกี่ยวข้อง จริง ๆ หากน้องย้อนอดีตไปตอนม.2 สมการพีทาโกรัส คือสามเหลี่ยมมุมฉาก ดังนั้นมุม C คือ 90 องศา (มุมฉาก) แต่ \(\cos{90^\circ}=0\) แปลว่า พจน์ \(\textcolor{blue}{-2ab\cos{C}}\) ก็เลยหายไป เอาจริง ๆ มันคือสูตรเดียวกันแหละ แต่กฎของโคไซน์ มีความ "Generalize" หรือในเชิงทั่วไป มากกว่า ก็คือใช้ได้กับสามเหลี่ยมทุกรูปนั่นเองครับ
ในเมื่อมันใช้กับมุมใด ๆ ก็ได้ แปลว่า เราก็สามารถใช้สูตรกับมุม A และมุม B ได้เช่นกัน ดังนี้ (มีสามสูตรที่จริง ๆ ไม่ต้องจำแยก น้องสามารถใช้หลักการเดียวกับ พีทาโกรัสในการจำได้เลย)
\(c^2=a^2+b^2\textcolor{blue}{-2ab\cos{C}}\)
\(b^2=a^2+c^2\textcolor{blue}{-2ac\cos{B}}\)
\(a^2=b^2+c^2\textcolor{blue}{-2bc\cos{A}}\)
เรื่องนี้สูตรง่าย และโจทย์ก็ออกได้ค่อนข้างหลากหลายดังนั้นพี่จะสอนโจทย์ในวิดีโอไปเลยทีเดียว ใครสนใจก็จิ้มที่วิดีโอข้างบนหน้านี้ได้เลยนะครับ
หากบทความพี่เป็นประโยชน์ ฝากแชร์ต่อให้เพื่อนๆ ด้วยนะครับ :')

