เลือกอ่านตามหัวข้อ?

เข้าหาบทความพี่ง่ายๆ จาก Google


ตรีโกณมิติ sin cos tan
หากน้องๆ จำได้ ใน ม.3 ที่เราเรียนกันในอัตราส่วนตรีโกณมิติ sin cos tan ที่เราท่องหรือร้องเพลงกันว่า ''sin คือ ข้ามฉาก cos คือ ชิดฉาก tan คือ ข้ามชิด'' อันนี้เป็นการประยุกต์ใช้ sin cos tan แบบง่ายกับสามเหลี่ยมมุมฉาก
ใน ตรีโกณมิติ ม.5 เราจะมาหาค่า sin cos tan แบบเยอะมุมมากขึ้น อย่างเช่น มุมที่มากกว่า 90 องศา ไปจนถึง มุมที่มากกว่า 360 องศา หรือมุมอื่นๆ ทั่วไป โดยการใช้ ''วงกลมหนึ่งหน่วย'' กันครับน้อง
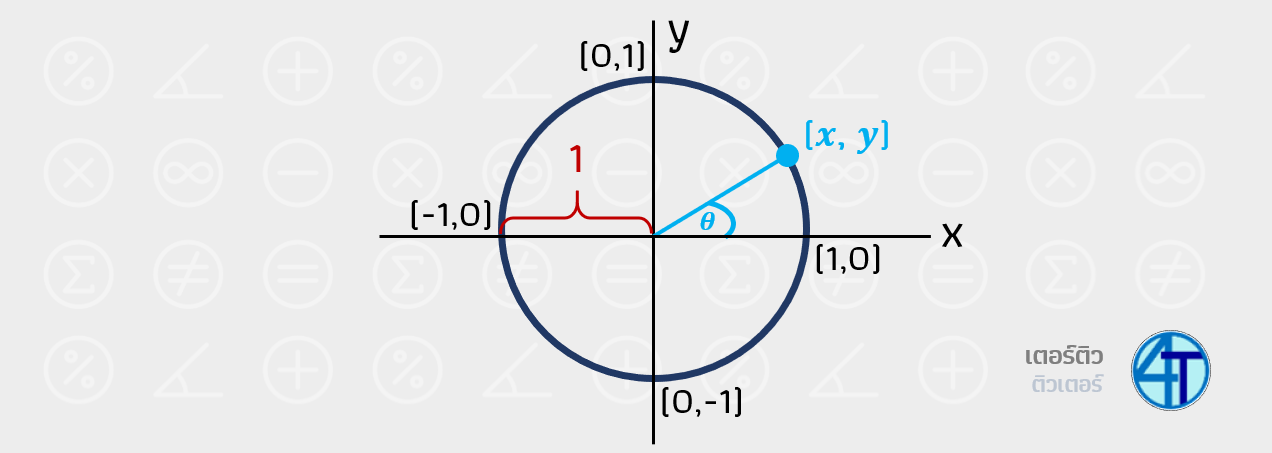
วงกลมหนึ่งหน่วย
จำกันได้หรือเปล่าจากพาร์ทที่แล้ว ว่าเราจะมีค่าสำคัญๆ สามตัวแปรด้วยกัน คือ \(\theta, x, y\) ซึ่งใน ตรีโกณมิติ ม.5 เราจะกำหนดให้ \(\sin(\theta)=y\) และ \(\cos(\theta)=x\)
ท่องว่า cos x sin y
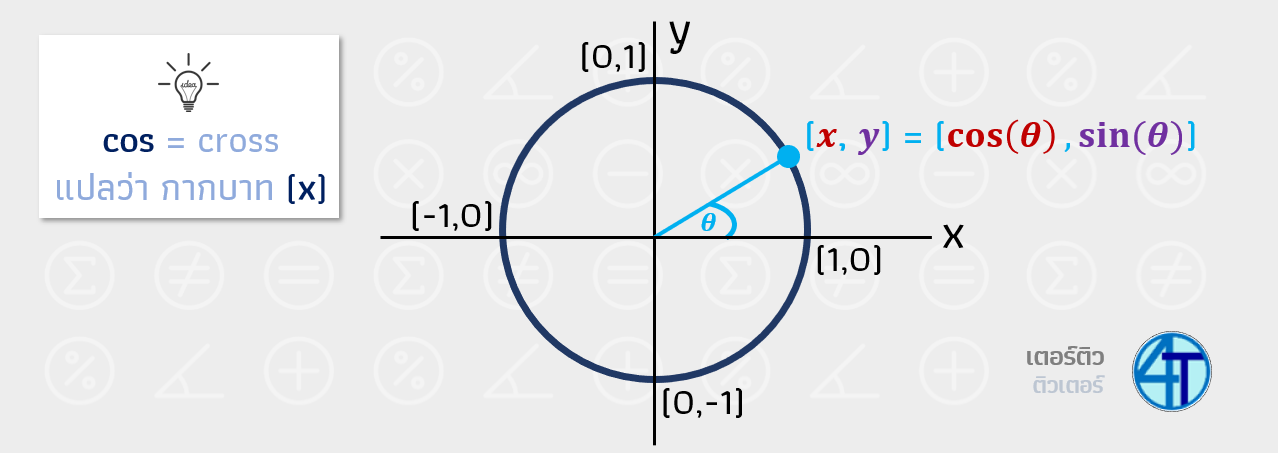
ทริคการจำง่ายๆ (มีความอินเตอร์นิดๆ) คือพี่ใช้วิธีนี้จำมาตลอดเลยคิดว่าน่าจะเป็นประโยชน์ดีสำหรับน้องๆ คือถ้าใครเผลอลืมจริงๆ ว่าเห้ย sin cos อันไหนคือ ค่า x หรือ y นะ ลองนึกถึง cos เป็นคำภาษาอังกฤษคำว่า cross ดูครับน้องๆ เวลาน้องๆ เอาอะไรมา cross กัน (ไขว้กัน) มันก็คือ เครื่องหมายกากบาท (cross) นั่นเอง กากบาทก็คือ x ดังนั้น cos จึงเป็นค่า x ส่วน sin เป็นค่า y อีกวิธีการจำอีกอันคือ sin (ทราย) คล้องจองกับ y (วาย)
ตัวอย่างกันงง: สมมติพี่มีภาพดังด้านล่าง และพี่ต้องการจะหาค่า x กับ y ที่มุม \(\theta =\,60^\circ\)
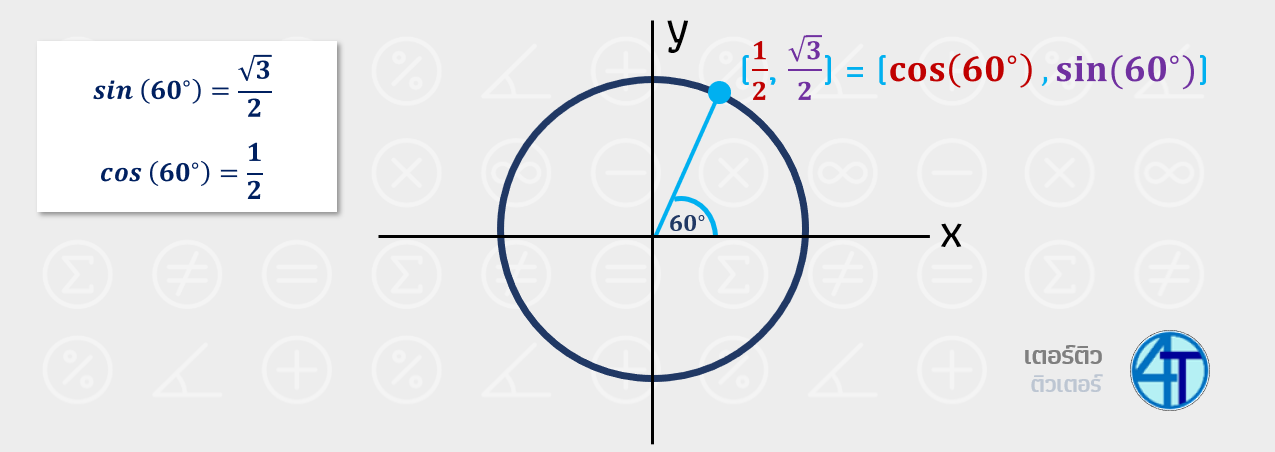
จากความรู้ อัตราส่วนตรีโกณมิติ ม.3 น้องๆ ได้เรียนกันไปแล้วว่า \(\sin(60^\circ)=\dfrac{\sqrt{3}}{2}\) และ \(\cos(60^\circ)=\dfrac{1}{2}\) ซึ่งค่า cos x sin y ดังนั้น ค่า \((x,y)=\left(\dfrac{1}{2},\dfrac{\sqrt{3}}{2}\right)\) นั่นเอง หลักการคือเราจะใช้มุมมาตรฐานที่เราเรียนมาตอน ม.3 มาหาค่า ตรีโกณมิติ ม.5 พวกค่า sin cos tan ของมุมอื่นๆ ในวงกลมนั่นเอง
มุมบนแกน X แกน Y
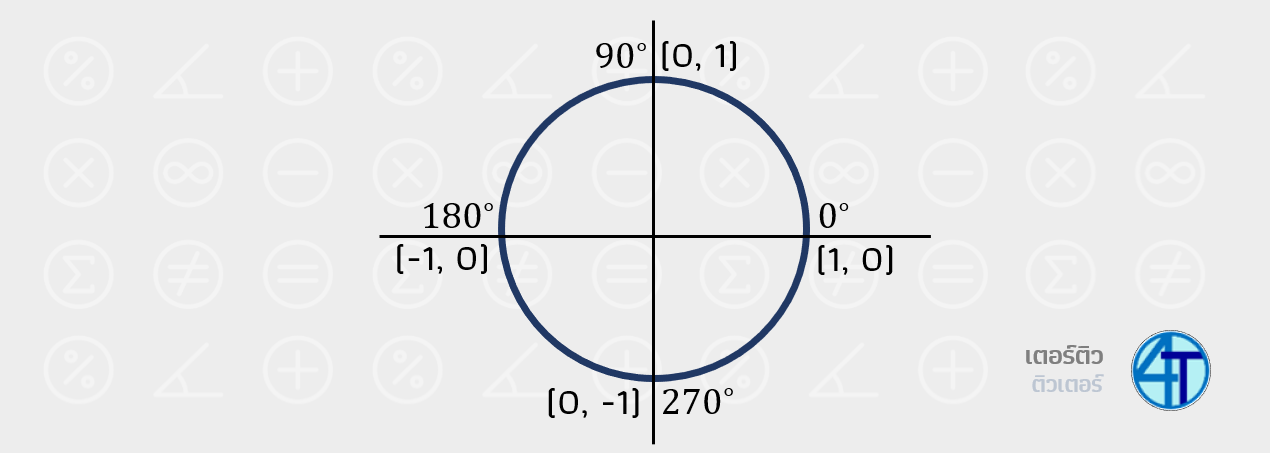
สำหรับมุมบนแกน ก็ไม่ยากครับน้องๆ ลองดูรูปด้านบนประกอบ สมมติพี่ให้โจทย์น้องหา \(\sin(90^\circ)\) สิ่งที่น้องต้องนึกในหัวคือ
- 1) หาค่า sin ก็คือ cos x sin y ดังนั้น น้องต้องหาค่าของ y
- 2) จุดบนวงกลมตอนน้องกวาดไป \(90^\circ\) คือจุดคู่อันดับ \((0,1)\) ดังนั้น ค่า \(y=1\) แปลว่า \(\sin(90^\circ)=1\)
จำได้หรือเปล่าว่าการเขียนมุมเขียนได้ 2 หน่วยด้วยกัน (1) องศา (2) เรเดียน ในพาร์ทวงกลมหนึ่งหน่วย ดังนั้น \(\sin(90^\circ)=1=\textcolor{blue}{\sin\left(\dfrac{\pi}{2}\right)}\) เพราะ 90 องศามีค่าเท่ากับ \(\dfrac{\pi}{2}\) เรเดียน
ลองอีกตัวอย่าง สมมติพี่ต้องการหาค่าของ \(\cos\left(\dfrac{3\pi}{2}\right)\) ในหัวน้องต้องคิดและว่าอยู่จุดไหน จุด \(270^\circ\) นั่นเองครับ ใครยังแปลง เรเดียนองศา ไม่แม่นกลับไปฝึกในพาร์ทที่แล้วก่อนนะ ซึ่งจุด \(270^\circ\) มีคู่อันดับบนวงกลมหนึ่งหน่วยคือ \((0,-1)\) ดังนั้นหาค่า cos จาก cos x sin y ได้ว่า เราต้องใช้ ค่าของ x ในการตอบ เพราะฉะนั้น \(\cos\left(\dfrac{3\pi}{2}\right)=0\)
(1) หาว่าจบตรงไหนของวงกลม
(2) หาคู่อันดับนั้น
(3) cos x sin y
มุมมาตรฐานนอกแกน
ให้สังเกตคำว่า มุมมาตรฐาน เวลาพี่พูดแบบนี้ มันคือมุมที่เราคุ้นเคยนั่นเองครับน้อง เช่นพวกที่เรียนตรีโกณมิติตอน ม.3 ได้แก่มุม \(30^\circ, 45^\circ, 60^\circ\) มุมพวกนี้เรารู้ค่าคำตอบอยู่แล้วจาก ตาราง sin cos tan ที่เรียนในอัตราส่วนตรีโกณมิติตอน ม.3 พี่หวังว่าน้องๆ คงจำกันได้ขึ้นใจกันแล้วนะ ถามปุ๊บตอบปั๊บ ได้ไรงี้
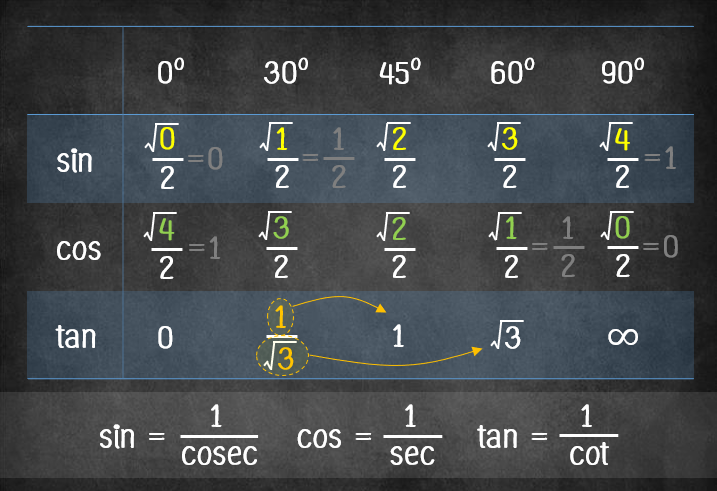
ทวนความจำวัยมัธยมต้น
แล้วมุมมาตรฐานที่พี่หมายถึงคืออะไรหละครับพี่ เพราะถ้างั้นเราก็ตอบได้เลยมั้ยจากตารางด้านบน? มุมมาตรฐานในที่นี้ พี่หมายถึง มุมที่มันอยู่ใน จตุภาคอื่นๆ ที่ไมใช่ จตุภาคที่ 1 หมายความว่า มุมมันไม่ได้อยู่ในช่วง \(0\leq\theta\leq\dfrac{\pi}{2}\) นั่นเอง แต่มันสามารถแปลงไปแปลงมา และใช้คำตอบที่เรารู้จากมุม \(0\leq\theta\leq\dfrac{\pi}{2}\) มาช่วยหาคำตอบได้นั่นเอง ตัวอย่างเช่น มุม \(225^\circ, 135^\circ\)
วิธีการก็ไม่ยากครับน้อง ใช้หลักการเดิม กับมุมบนแกนนั่นแหละ แต่ข้อแตกต่างคือ สมมติน้องหาได้แล้วว่ามันหยุดที่จุดไหน น้องจะยังไม่รู้ว่า คู่อันดับมันคือค่า x y อะไร เพราะ มันไม่เหมือนจุดบนแกนถูกมั้ยเอ่ย จุดบนแกนเรามองกราฟก็ออกและว่าจุดคืออะไร สมมติ ต้องการหา \(\sin(210^\circ)\)
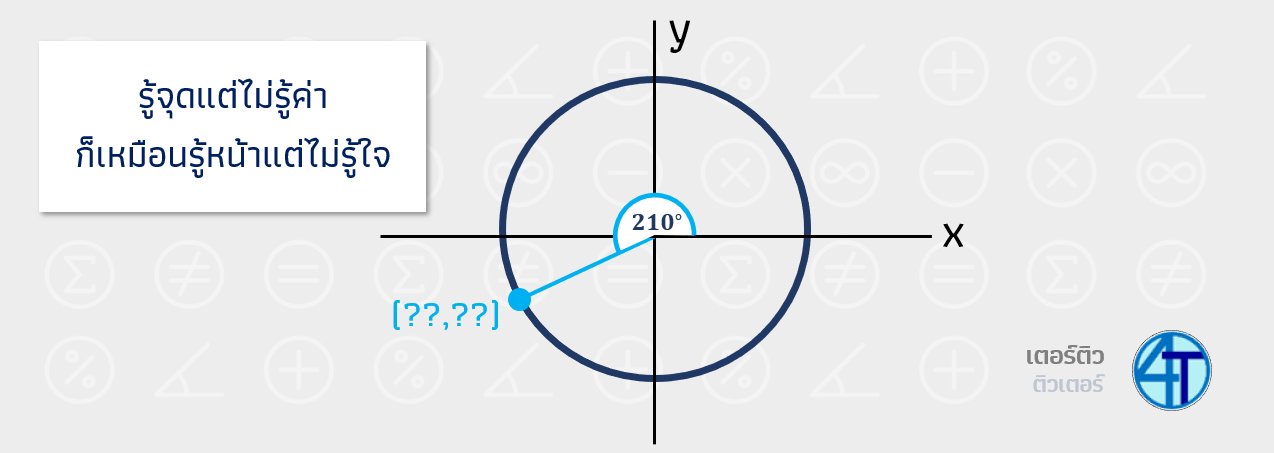
แต่ข้อดีของมุมมาตรฐานที่เราจะนำมาหาค่า sin cos tan ที่มันไม่อยู่ในจตุภาคที่ 1 เนี่ยมันคือ เราสามารถเขียนจุดมาตรฐานในจตุภาคที่ 1 ขึ้นมาได้ จากแกน X Y ที่อยู่ใกล้เคียงกับเรา

พี่ขอเรียกแกนใกล้เคียงว่า แกนเพื่อนบ้าน นะ เพื่อความเข้าใจง่าย จากรูปข้างบนพี่เลือกแกน X ตรง \(180^\circ\) ซึ่งจริงๆ น้องสามารถเลือกแกน Y ตรง \(270^\circ\) ก็ได้ครับ (แบบนี้ยากกว่า ดังนั้น แนะนำให้เอาแกน X เพื่อนบ้านในการหาคำตอบ) หลังจากนี้คือ ปกติเราจะท่องสูตรกันมหาศาลเลย ซึ่งข้อดีก็คือ อนาคตถ้าน้องเข้าใจหลักการ สูตรจะทำให้เราทำโจทย์ได้เร็วขึ้น แต่! ถ้าน้องลืมสูตร หรือจำคลาดเคลื่อน ทำผิดได้ง่ายๆ เลย ดังนั้น พี่ขอสอนวิธีคิดปกติก่อน พี่ที่ใช้มาตลอดจนจบป.ตรี ก็ไม่ต้องจำสูตร แต่ก็ยังทำได้อยู่ พอน้องเข้าใจวิธีคิดแล้ว ต่อไป จะไปจำสูตรหรือทริคเพื่อให้คิด ตรีโกณมิติ ได้เร็วขึ้น ก็ไม่ว่ากันครับ
(1) แกนเพื่อนบ้าน เมื่อน้องได้แกนเพื่อนบ้านแล้ว ให้น้องคำนวณส่วนต่าง จากภาพข้างบน พี่เลือกแกนเพื่อนบ้านคือ \(180^\circ\) ดังนั้นต้อง \(+30^\circ\) ให้ได้ \(210^\circ\) ตามที่เราต้องการหา
(2) สะท้อนไปจนถึงจตุภาคที่ 1 ให้น้องลากเส้นไปจนถึงจตุภาคที่ 1 ลากขนานแกน X และขนานแกน Y
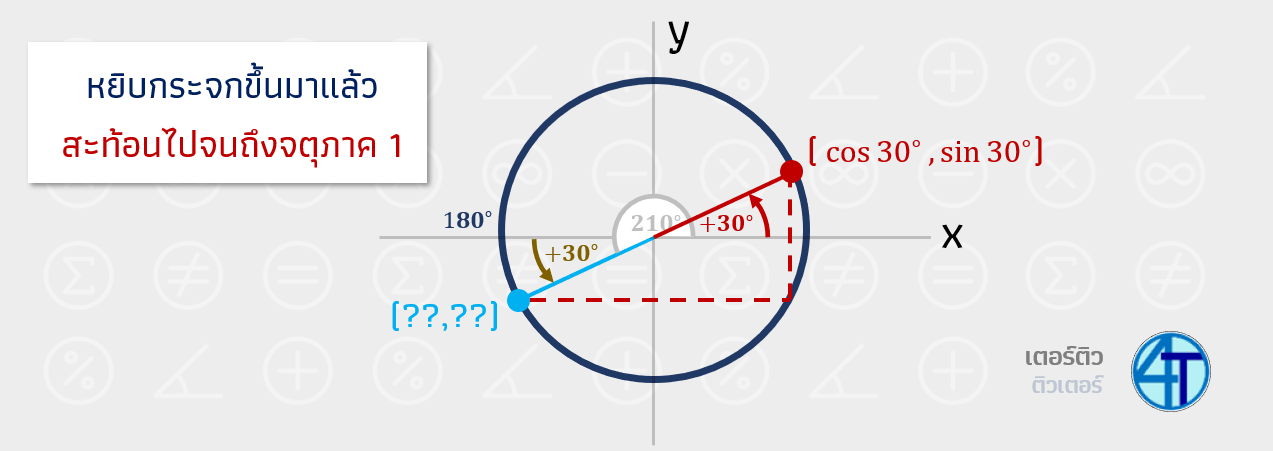
เมื่อสะท้อนแล้วน้องๆ จะได้จุดในจตุภาคที่ 1 ในมุมที่เรารู้ค่า sin cos นั่นเอง อยากข้างบน พอเราสะท้อนมุม \(210^\circ\) ไปเราก็จะได้มุม \(30^\circ\) ถามว่ารู้ได้ไงว่ามุมนั้นเป็นมุม \(30^\circ\)? ก็สังเกตจากรูปเลยครับ มุมตรงข้ามซึ่งกันและกัน
(3) จากนั้นค่อยๆ ไล่กลับ เพื่อหาค่า มุม \(210^\circ\) ของเรา
- ถ้าสะท้อนผ่านแกน X ค่า Y กลับเครื่องหมาย
- หากสะท้อนผ่านแกน Y ค่า X กลับเครื่องหมาย
การสะท้อนแกนข้างบนเป็นความรู้พื้นฐานนะครับ หากน้องๆ คนไหนยัง งงๆ ลองนึกภาพกราฟตามและลองคิดตามดูนะ
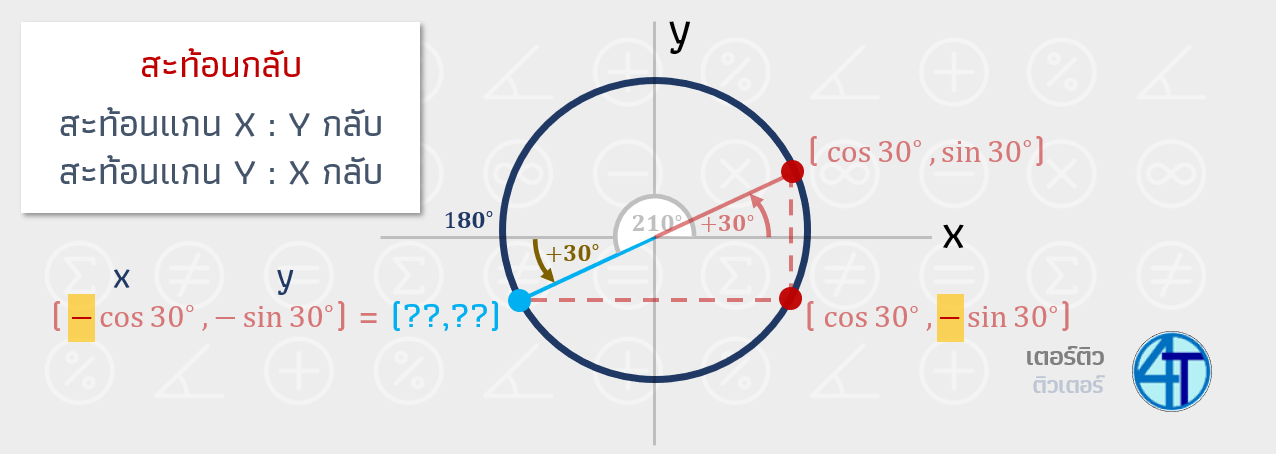
เมื่อน้องสะท้อนกลับมาน้องจะสังเกตเห็นว่า เราได้คำตอบของคู่อันดับตรงมุม \(210^\circ\) เรียบร้อย ซึ่งอยู่ในรูปของ มุม \(30^\circ\) จากโจทย์ถามว่า \(\sin(210^\circ)\) (อ่านมาตั้งนานลืมโจทย์กันไปยัง 5555+) แสดงว่าเราต้องหาค่า? y (ท่องให้ขึ้นใจ cos x sin y) ดังนั้น \(\sin(210^\circ)=-\sin(30^\circ)\) \(=-\dfrac{1}{2}\)
ซึ่งข้างบน น้องๆ จะเห็นว่า \(\sin(180^\circ+30^\circ)=-\sin(30^\circ)\) มันเป็นที่มาของสูตรนี้เลย ล้อกันมาลองสังเกตดู \(\textcolor{blue}{\sin(\pi+\theta)=-\sin(\theta)}\)
แถม: คืออุตส่าห์คิดมาและไงข้างบน สองพิกัดในคู่อันดับ \((x,y)\) หากเราต้องการหา \(\cos(210^\circ)\) คือตอบค่า x ดังนั้น \(\cos(210^\circ)=-\cos(30^\circ)=-\dfrac{\sqrt{3}}{2}\) ล้อกันมาเหมือนเดิมครับ \(\cos(180^\circ+30^\circ)=-\cos(30^\circ)\) ดังนั้น \(\textcolor{blue}{\cos(\pi+\theta)=-\cos(\theta)}\)
\(\sin(\pi+\theta)=-\sin(\theta)\)
\(\cos(\pi+\theta)=-\cos(\theta)\)
ขอรวบรัดเลย สังเกตว่า การใช้แกน X เพื่อนบ้านเนี่ย หากน้องต้องการหาค่า sin คำตอบสุดท้ายก็ยังเป็นค่า sin หากน้องจะหาค่า cos คำตอบสุดท้ายก็ยังใช้ค่า cos ดังนั้น ปกติแล้ว เราจะหาค่ามุม \(0^\circ\leq\theta\leq90^\circ\) ซึ่งเป็นมุมที่เราต้องการหากระทำกับแกน X เพื่อนบ้าน เช่น \(\sin(210^\circ)=\sin(180^\circ+30^\circ)\) ดังนั้น กรณีนี้ \(\theta=30^\circ\) ดังนั้นเราจะใช้ \(\sin(30^\circ)\) เพื่อตอบคำตอบของ \(\sin(210^\circ)\) และดูเครื่องหมายทีหลัง* ตามจตุภาค (tan ก็ใช้ได้เหมือนกันเนื่องจาก \(\tan=\dfrac{\sin}{\cos}\))
*คำถามต่อมาคือจะดูเครื่องหมายตามจตุภาคได้อย่างไร...
เครื่องหมาย sin cos tan ในแต่ละจตุภาค
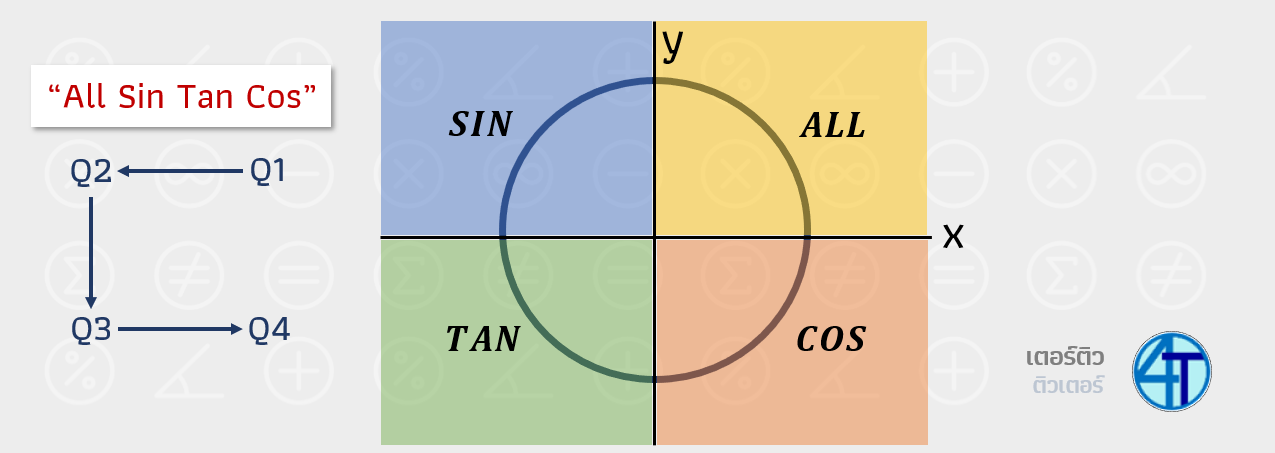
จริงๆ บทนี้ไม่ยากเลยครับน้องๆ เนื่องจากเรารู้ว่า cos x sin y ดังนั้น sin ก็จะเป็นบวกแค่ตอนที่ค่า y เป็นบวก (จตุภาค 1 และ 2) ส่วน cos ก็จะเป็นบวกแค่ตอนที่ค่า x เป็นบวก (จตุภาค 1 และ 4) ส่วน tan คือ sin หารด้วย cos ดังนั้นจะเป็นบวกก็ต่อเมื่อ ค่า x และ y มีเครื่องหมายเดียวกัน (+ หาร + ที่จตุภาค 1 และ - หาร - ที่จตุภาค 3)
ส่วนมากชอบท่องจำกันว่า ALL SIN TAN COS
- จตุภาค 1 บวกหมด (all)
- จตุภาค 2 sin บวกอย่างเดียว
- จตุภาค 3 tan บวกอย่างเดียว
- จตุภาค 4 cos บวกอย่างเดียว
กลับมาที่ตัวอย่างโจทย์ สมมติต้องการหา \(\sin(150^\circ)\) ขั้นแรกเราต้องเขียนในรูป เพื่อนบ้านแกน X (\(180^\circ\)) จะได้ว่า \(\sin(150^\circ)=\sin(180^\circ-30^\circ)\) ดังนั้น \(\theta=30^\circ\) เราจะได้คำตอบของ \(\sin(150^\circ)=\textcolor{blue}{?}\sin(30^\circ)\)
เติมเครื่องหมายใน \(\textcolor{blue}{?}\) สิ มุม \(150^\circ\) อยู่ในจตุภาคที่ 2 ดังนั้นค่า sin เป็นบวก \(\sin(150^\circ)=\textcolor{blue}{+}\sin(30^\circ)=\dfrac{1}{2}\)
ง่ายม้ะน้องๆ แค่ 2-3 บรรทัดก็เสร็จและ
การเข้าใจไอเดียว่าสูตรมายังไง จะทำให้น้อง ทำคณิตฯ ได้อย่างเข้าใจในระยะยาว
มุมเกิน \(2\pi\)
อย่างที่บอกไปในพาร์ทที่แล้วว่า \(2\pi\) คือหนึ่งรอบวงกลม ดังนั้นหากน้องได้มุมเกิน \(2\pi\) ในตรีโกณมิติ เราสามารถลดทอนมุมนั้น ออกทุกๆ \(2\pi\) ไปเรื่อยๆ ได้ จนกว่าจะได้มุมที่น้อยกว่า \(2\pi\) เช่น หากให้หาค่า \(\cos(9\pi)=\cos(2\pi\textcolor{blue}{\times4}+\pi)\) พี่สามารถดึง \(2\pi\) ออกมาได้ตั้ง 4 รอบแหนะ แปลว่า \(\cos(9\pi)=\cos(\pi)\) เพราะการหมุนรอบวงกลมแล้วกลับมาที่เดิม มันไม่ส่งผลอะไรเลย เราสามารถละทิ้งได้
\(\sin(2n\pi+\theta)=\sin(\theta)\)
\(\cos(2n\pi+\theta)=\cos(\theta)\)
\(\tan(2n\pi+\theta)=\tan(\theta)\)
ทุกๆ \(2n\pi\) (\(n\) คือจำนวนรอบที่หมุนรอบวงกลม) เราสามารถละทิ้งได้ สมการข้างบนเราจะหาค่า \(n\) มากสุดมาตัดทอน โดยที่ \(0\leq\theta\lt2n\)
มุมติดลบ
จริงๆ มองไม่ยากครับน้องๆ ให้น้องลองนึกภาพตามพี่ว่า เห้ยแทนที่เราจะกวาดมุมจากแกน X ขึ้นไป (มุมบวก) เราดันกวาดจากแกน X ลงมาแทน (มุมลบ) ดังนั้นจุดที่น้องได้มันจะสลับด้านกัน โดยมีแกน X เป็นตัวสะท้อน ดังนั้นเมื่อน้องรู้แล้วว่า แกน X สะท้อน แสดงว่า ค่าจุดพิกัดที่เราได้ ค่า X เท่าเดิม แต่ค่า Y กลับด้าน ซึ่ง ''cos x sin y'' ดังนั้น หากกลับมุมจากลบเป็นบวก cos เท่าเดิม ส่วน sin กลับด้าน นั่นเอง
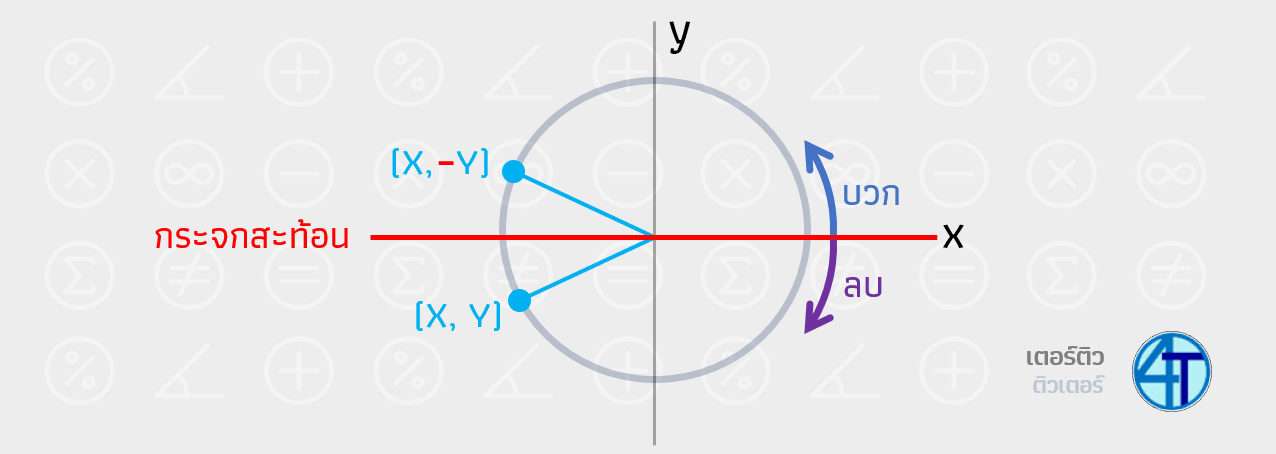
\(\sin(-\theta)=-\sin(\theta)\)
\(\cos(-\theta)=\cos(\theta)\)
ทีนี้ก็ไม่ยากและ จริงๆ จำแค่สองตัวข้างบนก็พอแล้ว เพราะถ้าเราต้องการหา \(\tan(-\theta)\) เราก็ตั้งสมการได้เลยว่า tan คือ sin ส่วน cos ฉะนั้น \(\tan(-\theta)=\dfrac{\sin(-\theta)}{\cos(-\theta)}\)\(\,=\dfrac{-\sin(\theta)}{\cos(\theta)}=-\tan(\theta)\)
\(\tan(-\theta)=-\tan(\theta)\)

หากบทความพี่เป็นประโยชน์ ฝากแชร์ต่อให้เพื่อนๆ ด้วยนะครับ :')

