เลือกอ่านตามหัวข้อ?
เข้าหาบทความพี่ง่ายๆ จาก Google


วงกลม 1 หน่วย มีความสำคัญอย่างไร ในตรีโกณมิติ ม.5
หากน้องๆ ยังจำกันได้ในเรื่อง อัตราส่วนตรีโกณมิติ ม.3 ที่เรียนกันไปกันแบบง่ายๆ บทตรีโกณมิติ ม.5 นี้ก็คือ ร่างใหม่ที่เพิ่มเติมไปด้วยความยากและหิน จนบทนี้ได้ถูกขนานนามกันว่า เป็นบทเรียนคณิตม.ปลายเรื่องที่ยากที่สุดเรื่องหนึ่งเลยก็ว่าได้ แต่...อย่าพึ่งท้อถอยครับน้อง เพราะ เจ้าวงกลมหนึ่งหน่วย เนี่ย พี่ขอให้มันเป็นพระเอกของบทนี้เลย เพราะ หากน้องรู้คอนเซปต์ของวงกลมหนึ่งหน่วย น้องจะหามุมต่างๆ ของตรีโกณได้ด้วยความเข้าใจ และไม่ต้องท่องจำสูตรร้อยแปดพันเก้า
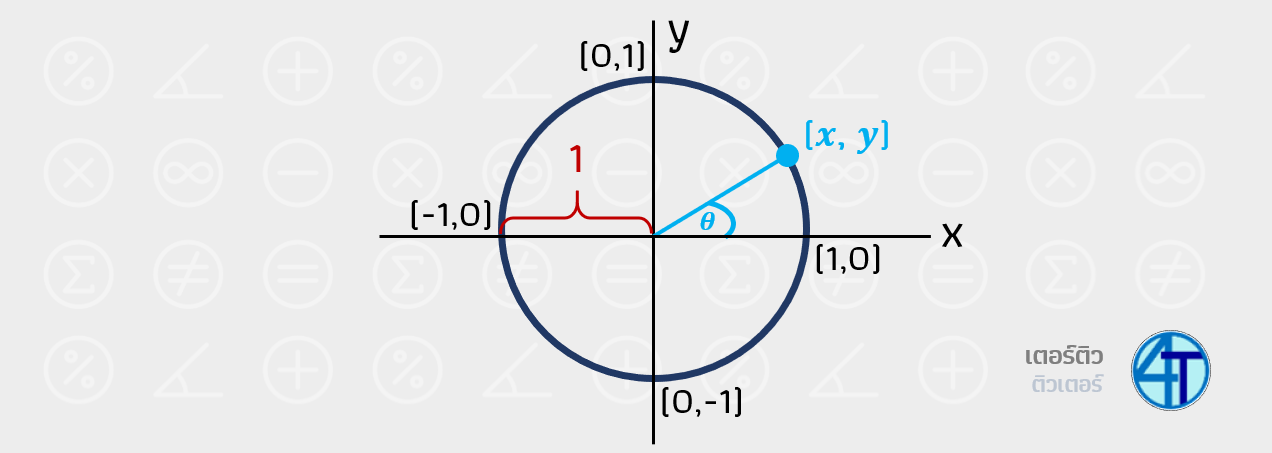
จากภาพด้านบน นี่คือวงกลมครับน้อง ที่มี รัศมี 1 หน่วย และมีจุดศูนย์กลางอยู่ที่ \((0,0)\) ให้เราสังเกตที่เส้นสีฟ้าที่พี่ลากอยู่ในวงกลม เมื่อเราทำการลาก จุดในวงกลมไม่ว่าจะตำแหน่งไหนก็ตาม สิ่งที่เราจะได้คือ
- มุมนับจากเส้นแกน X เรียกว่ามุม \(\theta\) (อ่านว่าเซต้า)
- จุดฟ้า ที่อยู่บนวงกลมพอดี ตำแหน่ง \((x,y)\)
อย่างที่น้องเดากันแหละครับ สามตัวนี้ \(\theta\), \(x\), \(y\) จะมีส่วนเชื่อมกับ ''ตรีโกณมิติ ม.5'' ที่เราจะเรียนกันต่อไป แต่ก่อนเข้าสู่ตรีโกณอย่างจริงจัง เราต้องรู้จักกับ มุม \((\theta)\) กันให้มากกว่านี้ก่อน
มุมในวงกลมตรีโกณ
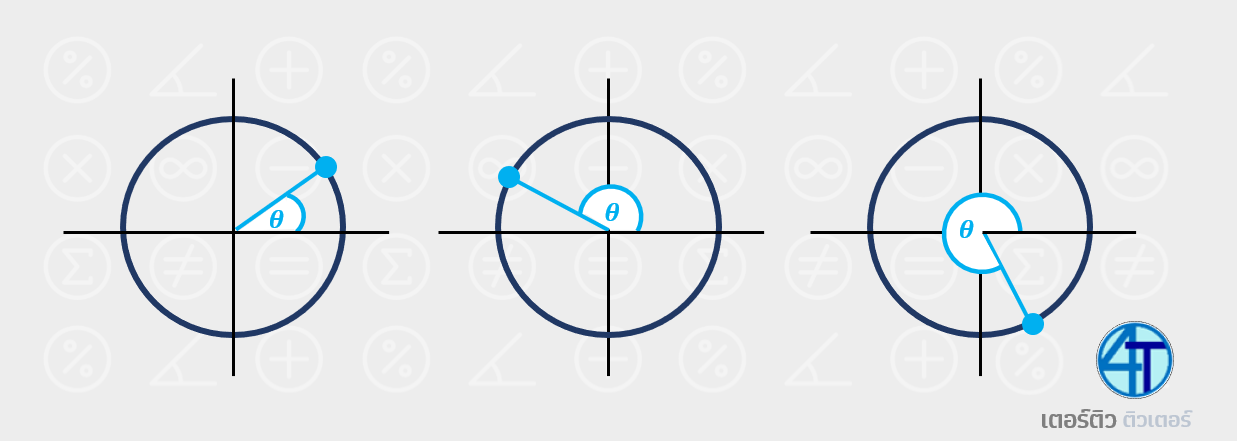
ตัวอย่างมุมในหลายๆแบบ
สำหรับ ค่ามุม ที่เราวัดได้ น้องสามารถใช้ได้ 2 หน่วยวัด
- องศา เช่น \(30^\circ,\,90^\circ,\,120^\circ,\dots\)
- เรเดียน
สำหรับ (1) องศา พี่เชื่อว่าคงไม่มีใครงงแน่นอน เพราะมันก็ตรงตัว ตามที่น้องๆ เคยเรียนกันมาในบทเรขาคณิตวิเคราะห์ เริ่มต้นที่ 0 พอน้องลากไปถึงแกน Y ก็จะได้ 90 องศาเพราะมันตั้งฉากพอดี ต่อไปอีกก็ 180 และ 270 ไปเรื่อยๆ

แต่แบบ เรเดียน คืออะไร? ก่อนอื่นต้องเข้าใจนิยามก่อน เรเดียน คือค่าตัวเลขที่คำนวณจาก ความยาวส่วนโค้งหารด้วยรัศมี

ดูรูปข้างบนประกอบนะครับน้องๆ สมมติพี่ต้องการหาค่า \(\theta\) แบบที่เป็นเลขทั่วไป ไม่ใช่หน่วยองศา เนื่องจากมุม \(\theta\) นั่นกวาดความยาวส่วนโค้งไปได้ทั้งหมด \(s\) หน่วย และรัศมีที่เราใช้ในวงกลมนี้คือ \(r\) ดังนั้นจากสมการที่ว่า เรเดียน คือค่าตัวเลขที่คำนวณจาก ความยาวส่วนโค้งหารด้วยรัศมี เราจึงได้ \(\theta=\dfrac{s}{r}\)
ดังนั้นเราจึงต้องหาความสัมพันธ์กันต่อว่า สมมติเรามีมุม \(x\) องศา มันจะเท่ากับกี่เรเดียน? หลักการที่แนะนำคือลองมองมุม \(360^\circ\) ก่อน
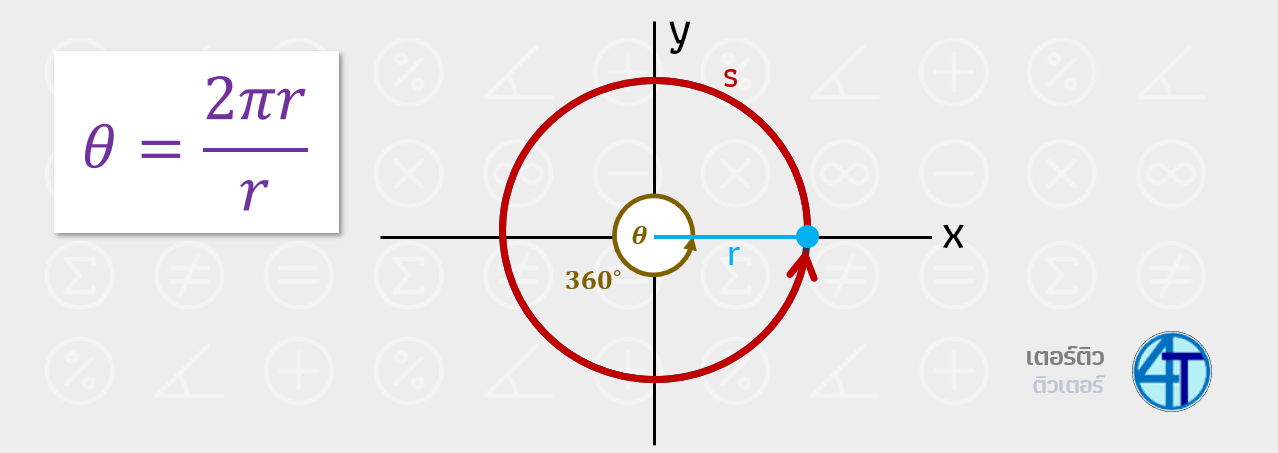
มุม \(360^\circ\) มันก็คือการที่เรากวาดไปทั้งวงกลมเลย ตามเส้นสีแดง แปลว่าระยะทั้งหมดที่กวาดได้ (ความยาวส่วนโค้ง) คือ ความยาวรอบรูปวงกลม ซึ่งมีค่าตามสูตรวงกลมว่า \(2\pi r\) หมายความว่าเราต้องแทน \(s=2\pi r\) และนำไปหารด้วยรัศมีเพื่อที่จะได้ มุมเรเดียน เราจึงได้สมการ \(360^\circ=\dfrac{2\pi r}{r}=2\pi\)
หากเราจับสมการ \(360^\circ=2\pi\) มาตัดทอนลงไปอีกโดยการหารด้วย 2 ทั้งสองข้าง เราจะได้ว่า \(180^\circ=\pi\) ตามที่น้องๆ เข้าใจกันนั่นแหละครับ \(\pi\) ที่มีค่า 3.14159265357989...
\(180^\circ=\pi\) เรเดียน
แถม: บางทีเราก็อาจจะเจอโจทย์เกรียนโดยการให้อีกสองหน่วยมุมย่อย ลิปดา (') กับ ฟิลิปดา ('') เราแค่ต้องรู้ว่า 1 องศาเท่ากับ 60 ลิปดา และ 1 ลิปดาเท่ากับ 60 ฟิลิปดา จากนั้นก็ใช้พวกนี้แปลงหน่วยง่ายๆ
มุมติดลบ กับ มุมเกิน 360 องศา
มุมเกิน 360 องศา (หรือเกิน \(2\pi\) เรเดียน)
พี่ขอเริ่มจาก มุมเกิน \(360^\circ\) และกันครับ หากน้องๆ จำได้หัวข้อข้างบนที่พี่บอกเรื่องกวาดมุมในวงกลมตรีโกณมิติไปนั้น เวลาน้องจะกวาดมุมใน วงกลม 1 หน่วย เนี่ยหากครบ 1 รอบและกลับมาที่เดิมแปลว่าน้องหมุนได้ครบ \(360^\circ\) ถูกมั้ยเอ่ย ดังนั้นไอเดียก็คือ หากเรามีมุมที่เกิน \(360^\circ\) รูปการหมุนมันก็จะกลับมาเหมือนเดิมแบบวนลูปนั่นเอง
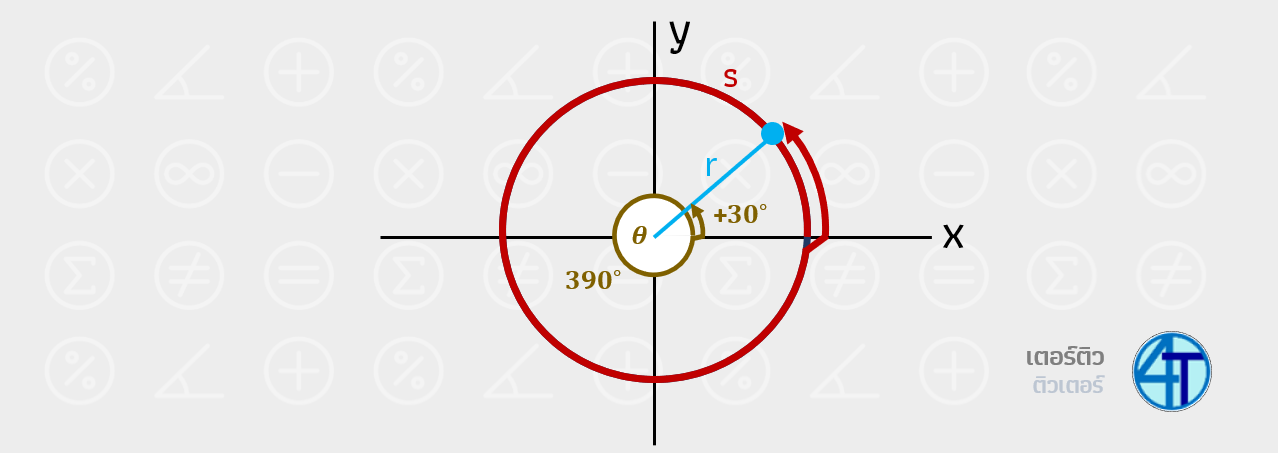
หากสังเกตตัวอย่างรูปด้านบนดีๆ การกวาดมุมไป \(390^\circ\) มันก็ไม่ต่างอะไรกับกวาดแค่ \(30^\circ\) เลย เพราะพอวนครบวงกลม 1 รอบมันก็กลับมาจุดเริ่มต้น และเราเสียไป 360 จาก 390 ดังนั้นก็หมุนอีก \(30^\circ\)
มุมติดลบ
ปกติที่กวาดมุมจากที่กล่าวมาข้างบนทั้งหมด เราจะกวาดเริ่มจาก แกน X ขึ้นไป หากในทางกลับกันน้องเลือกที่จะกวาดจาก แกน X ลงมา แบบนี้เราจะได้มุมค่าลบแทน
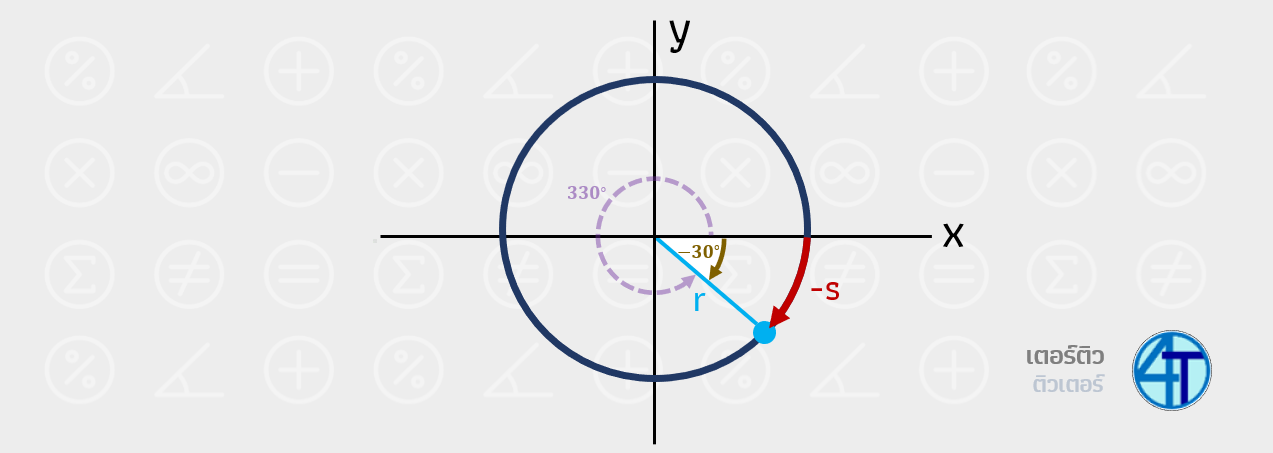
ตามภาพเลยครับ หากเราใช้การกวาดมุม \(330^\circ\) ตามเส้นประสีม่วงแบบปกติ แต่เราวัดแบบมุมติดลบแทน (วัดจากแก X ลงมา) เราจะได้มุมเป็นค่าลบ (รวมถึงความยาวส่วนโค้ง \(s\) ที่เราใช้ในสูตรการหา มุมแบบเรเดียน ด้วย)
ดังนั้น หากพี่ให้โจทย์น้องไปสองคน น้อง A กับน้อง B โดยให้น้อง A กวาดมุม \(-30^\circ\) ส่วนน้อง B กวาดมุม \(330^\circ\) และลากแค่เส้นสีฟ้าที่กวาดได้ส่งพี่ คำตอบของน้องทั้งสองก็จะเหมือนกันนั่นเอง พอเห็นภาพเนอะ

หากบทความพี่เป็นประโยชน์ ฝากแชร์ต่อให้เพื่อนๆ ด้วยนะครับ :')
