เลือกอ่านตามหัวข้อ?
กราฟของฟังก์ชันตรีโกณมิติ แบบ Interactive
ดูในคอมพิวเตอร์เพื่อภาพที่เต็มจอ (หากดูในโทรศัพท์สามารถเลื่อนไปทางขวาเพื่อดูกราฟได้ครับ หรือ ปรับโทรศัพท์เป็นแนวนอนเพื่อภาพที่เต็มจอ)
ขอบคุณ MathWarehouse สำหรับโปรแกรม Interactive
กราฟของฟังก์ชันตรีโกณมิติ sin กับ cos
พี่ขอเริ่มบทด้วยตรีโกณมิติตัวพื้นฐาน นั่นก็คือ sin กับ cos และกัน เนื่องจาก กราฟของทั้งคู่มีความสัมพันธ์กันสูง พี่จึง ขอจับรวมทั้งสองเข้าด้วยกัน เพื่อให้น้องเรียนไปแบบคู่ขนาน จะได้เห็นภาพความสัมพันธ์ต่างๆ ได้ง่ายขึ้นครับ
ทวนความจำ
การวาดกราฟของฟังก์ชัน โดยปกติแล้วหากเรามี \(y= \) อะไรสักอย่างในรูป \(x\) เช่น \(y=x^2\) หรือ \(y=\sqrt{x}\) ก็ตาม เราจะวาดกราฟโดยการใส่ค่า x ไปเยอะๆ และ แต่ละค่า x ก็จะได้จุด y ออกมา เราจะนำ (x,y) มาพล็อตลงบนกราฟนั่นเอง

ในเรื่องกราฟตรีโกณมิติ พี่บอกกันไปแล้วว่า มุม \(\theta\) คือ Input ส่วน Output (ผลลัพธ์) ก็คือ \(sin(\theta)\) นั่นเอง ดังนั้นจากภาพด้านบน หากเราเลือกค่ามุมตัวอย่างออกมา และพล็อต \(sin(\theta)\) ซึ่งคือค่าคู่พิกัด y ในวงกลม 1 หน่วย น้องจะสังเกตเห็นแพทเทิร์นคร่าวๆ ว่า กราฟ sin จะเป็น ลักษณะคล้ายๆ ลูกคลื่น โดยจุดเริ่มคือ 0 เนื่องจาก \(sin(0)=0\)
ต่อมาเราจะมาดูกันที่กราฟ cos ซึ่งอาจจะมองยากกว่ากราฟ sin นิดนึงครับน้องๆ ตรงที่ว่าการวัดค่า x มันไม่สามารถลากเส้นยาวมาเพื่อวาดกราฟเหมือน sin ข้างบนได้ ให้น้องๆ ลองจินตนาการโดยใช้ เส้นสีชมพู เป็นแกนหลัก และเส้นที่เคลื่อนที่ทะลุผ่านไป ออกยังอีกกราฟหนึ่ง ดังภาพเคลื่อนไหวด้านล่าง
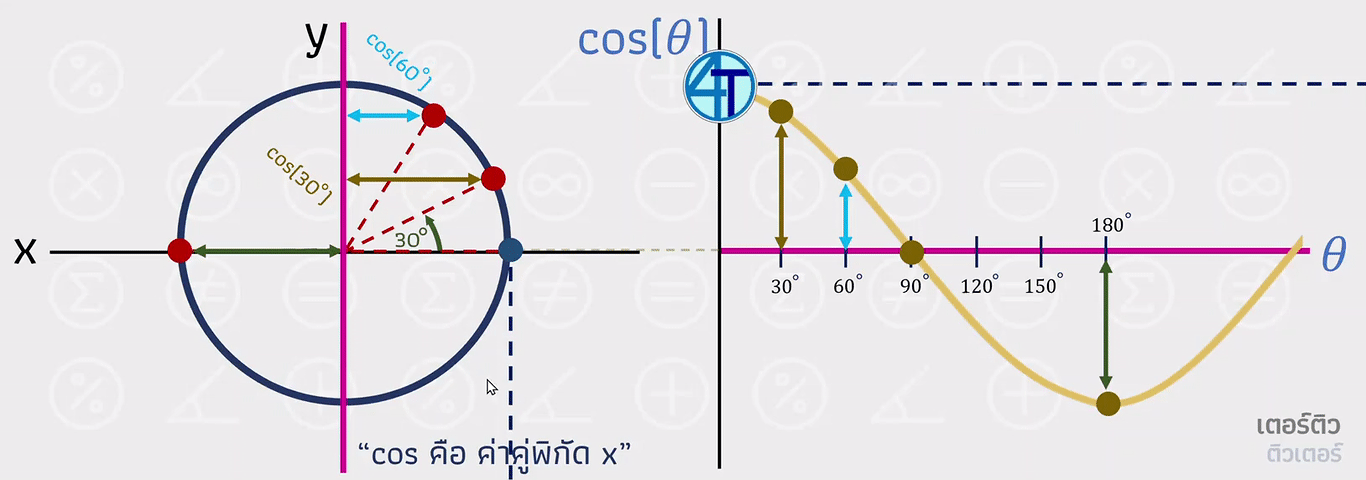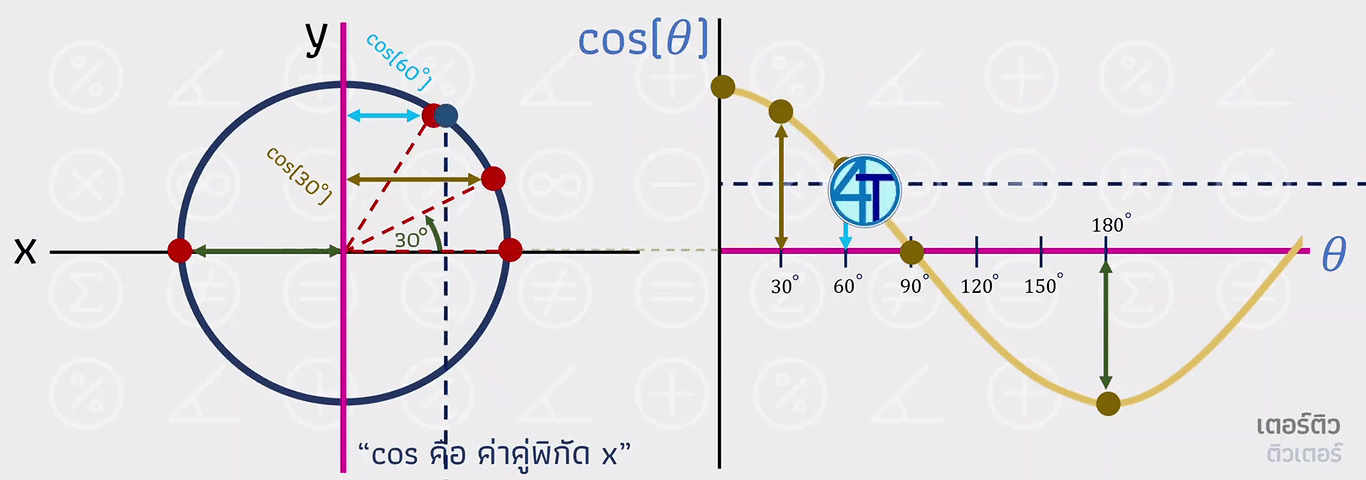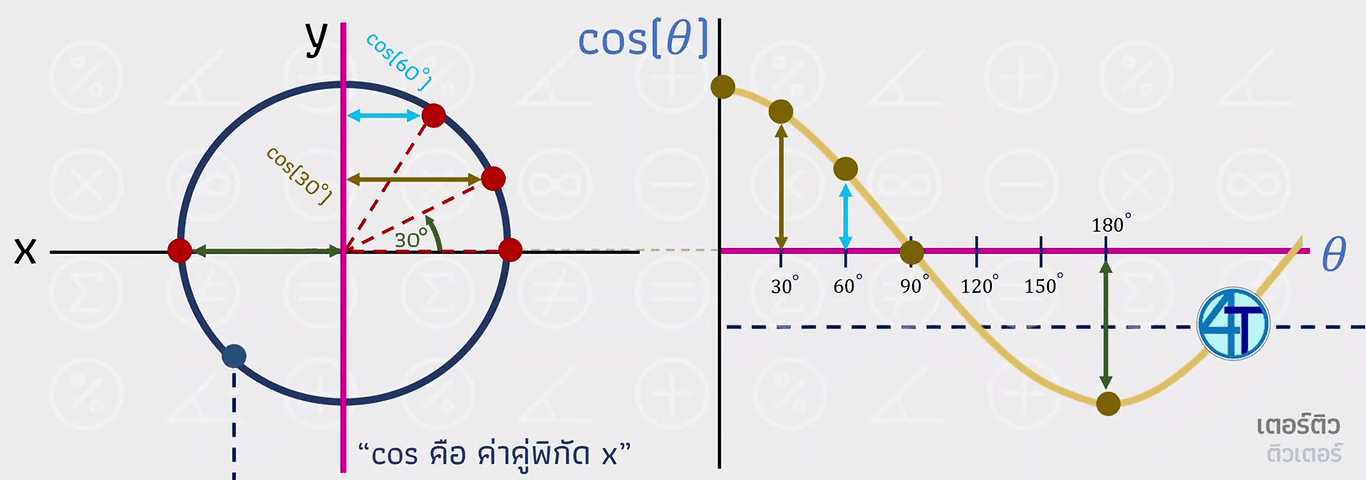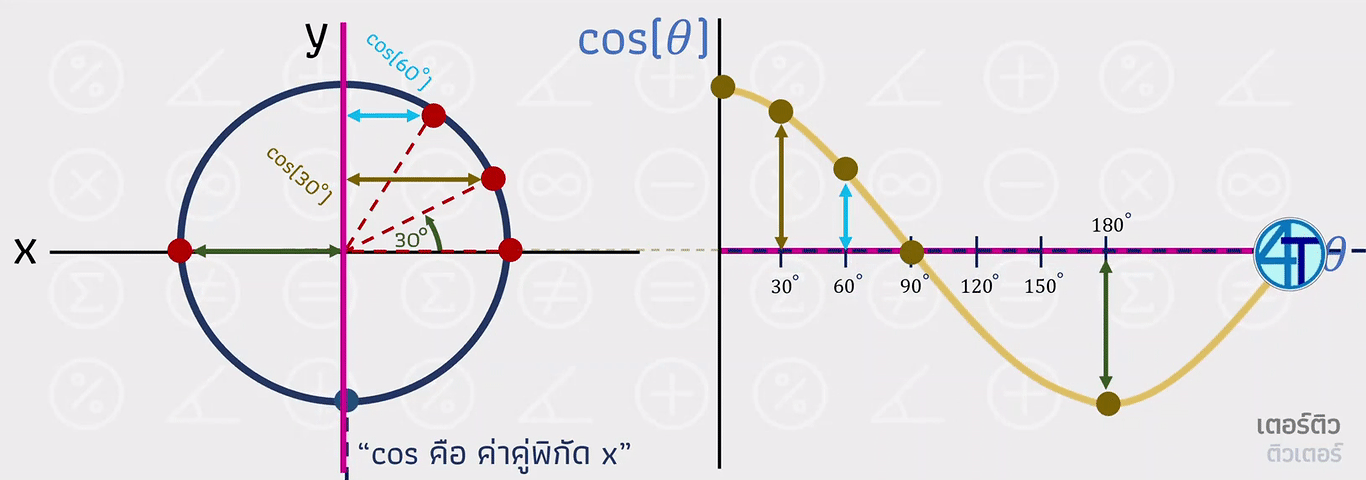
สรุปง่ายๆ ก็คือกราฟ cos มีรูปเป็นคลื่นเหมือนกับกราฟ sin แต่จะ เริ่มที่ 1 เนื่องจาก cos(0)=1 นั่นเองครับน้องๆ
เมื่อเรานำทั้งสองกราฟมารวมกัน เราจะเห็นได้ว่ากราฟมันเหมือนกันเลย แค่ เลื่อนกราฟซ้ายขวา เท่านั้นเอง เราจะดูกันครับว่า ในกราฟ sin กับ cos ที่เราวาดกันออกมานี้ มีอะไรที่น่าสนใจ (+คำศัพท์ที่น้องควรรู้) อะไรอยู่บ้าง
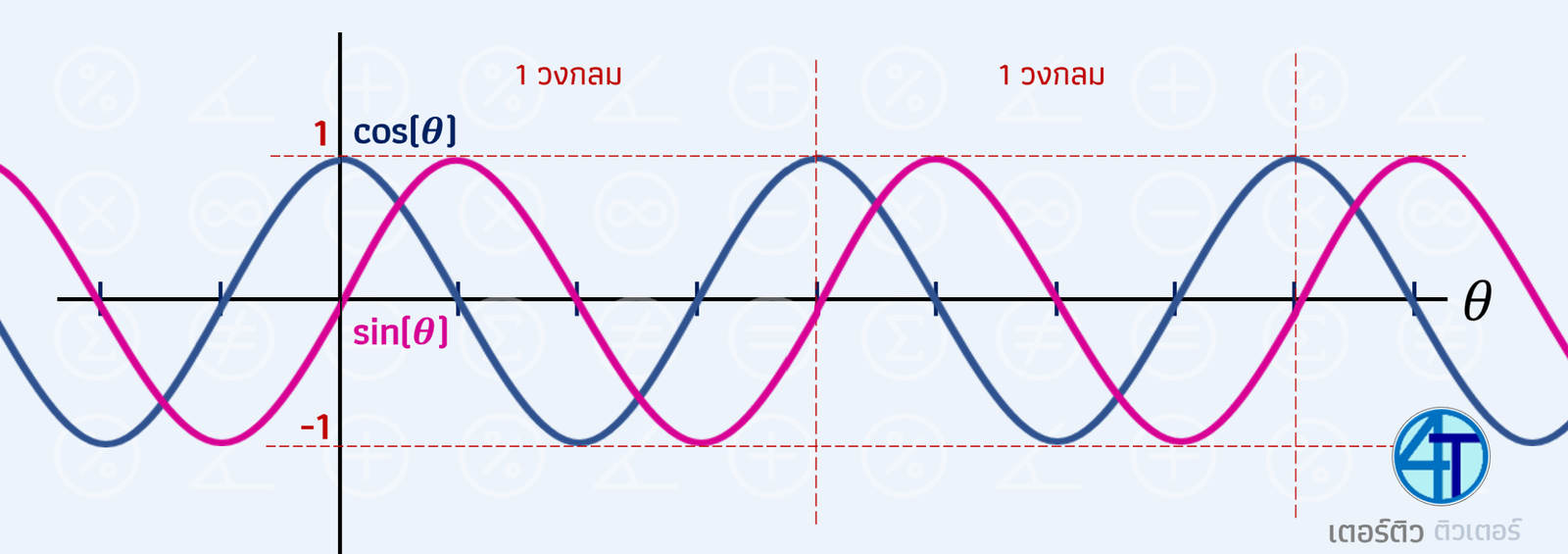
คาบ และ แอมพลิจูด
** ต่อไปนี้พี่จะพูดอ้างอิงถึง \(\color{blue}{\sin(\theta)}\) กับ \(\color{blue}{cos(\theta)}\) ก่อนเพื่อความง่าย และในส่วนต่อไปเราจะมาพูดถึงว่าถ้าเรามีตัวเลขแทรกอยู่ในสมการ ค่าพวกนี้ (คาบ, แอมพลิจูด) จะเปลี่ยนไปอย่างไร เช่น \(3sin(\theta)\) หรือ \(cos(4\theta)\)
1. คาบ
คาบ เราเรียกฟังก์ชันที่เกิดขึ้นซ้ำๆ กันว่า ฟังก์ชันเป็นคาบ (Periodic Function) ถามว่าแล้ว sin กับ cos มันเป็นฟังก์ชันคาบหรือไม่? ใช่แล้วครับน้องๆ มันเป็นฟังก์ชันแบบคาบ เนื่องจาก ทุกๆ 1 วงกลมทุกอย่างจะกลับมาเหมือนเดิม เหมือนตอนเริ่มที่ 0 (น้องสามารถสังเกตที่เส้นประแนวตั้งกันได้จากรูปด้านบน ว่าทุกๆ 1 วงกลม กราฟจะกลับมาเป็นเหมือนเดิมเลย) คาบก็คือ ช่วงที่กราฟจะกลับมาทำรูปแบบซ้ำเดิม
2. แอมพลิจูด
แอมพลิจูด คือค่าความแกว่งของกราฟ โดยวัดจาก จุดกึ่งกลาง ไปยังจุด ต่ำ-สูงสุดของกราฟ อย่างตัวอย่างกราฟด้านบน \(\color{blue}{sin(\theta})\) กับ \(\color{blue}{cos(\theta)}\) แกว่งอยู่ในช่วง [-1, 1] ดังนั้น ...
แอมพลิจูด มองได้อีกอย่างหนึ่งคือ (สูงสุด - ต่ำสุด) / 2
กราฟ sin cos แบบมีตัวเลขเพิ่ม feat. คาบและแอมพลิจูด
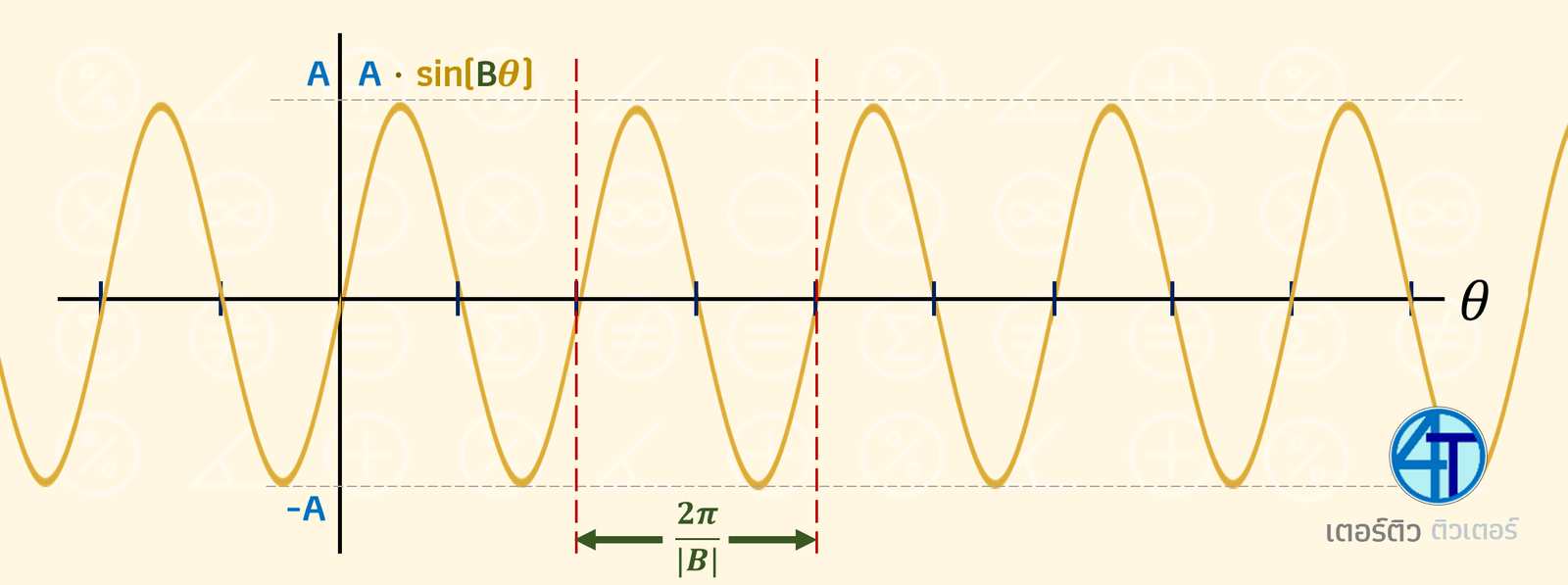
พี่เชื่อว่าน้องทุกคนเคยเจอ ฟังก์ชันพวกนี้ \(sin(4\theta)\), \(-2sin(2\theta)\), \(2cos(\theta+\pi)\) ซึ่งแน่นอนครับน้อง ตรีโกณมิติ ไม่ใช่มีแค่ sin cos หรือฟังก์ชันอื่นๆ แบบธรรมดา เราสามารถใส่ ตัวเลข เพื่อบวกลบคูณหาร ตรงไหนก็ได้ เราจะมาดูกันว่าแต่ละแบบ จะทำให้กราฟที่ได้แตกต่างกันออกไปยังไงได้บ้าง
1. มีตัวเลขคูณอยู่ข้างหน้า
\(\textcolor{blue}{a}\,sin(\theta)\)
เนื่องจากเรารู้แล้วว่า sin กับ cos ให้ ผลลัพธ์ เป็นค่าในช่วง [-1, 1] (เรนจ์ของ sin กับ cos) เมื่อเรานำ a ไปคูณ ก็เหมือนเป็นการ ขยาย หรือ scale ค่าที่ได้ไป a เท่า นั่นเอง เราก็จะได้ว่าผลลัพธ์ของ sin cos ก็จะขยาย จาก [-1, 1] กลายเป็น [-a, a]

ดังนั้นมันเป็นการขยาย (หรือหด) ตามค่าแกน y นั่นเองครับน้องๆ หากสังเกตดีๆ จะเห็นว่า
คาบ คือรอบที่กราฟกลับมาทำรูปแบบเดิมๆ ซึ่งการที่มันจะกลับมาทำรูปแบบเดิมๆ เรามองถึงแกน x เป็นหลัก ดังนั้นการที่เรา ขยาย/หด แกน y จะ ไม่มีผลกระทบต่อ คาบ ของฟังก์ชันนั่นเอง
แอมพลิจูด (ค่าสูงสุด - ค่าต่ำสุด) หารด้วย 2 เราลองคิดแบบไม่รู้อะไรเลยก็ได้ ตอนแรก แอมพลิจูดของ sin กับ cos คือ \(\dfrac{1 - (-1)}{2} = \dfrac{2}{2}\) = 1 พอเราขยายไป a เท่าค่าสูงสุดเปลี่ยนเป็น a และค่าต่ำสุดเปลี่ยนเป็น -a ดังนั้น แอมพลิจูด กลายเป็น \(\dfrac{a - (-a)}{2} = \dfrac{2a}{a}\) = a น้องจะเห็นว่า ค่าแอมพลิจูดก็เปลี่ยนไป a เท่าเช่นกัน ใช่แล้วครับน้อง การขยายกราฟ a เท่าค่า แอมพลิจูดก็จะเปลี่ยนไป a เท่าด้วยเช่นกัน
จากการสังเกต กราฟ \(a\,sin(\theta)\) กับ \(a\,cos(\theta)\) เราจะได้ว่าแอมพลิจูดจะเท่ากับ \(|a|\)
กราฟ \(\textcolor{red}{a}\,sin(\theta)\) กับ \(a\,cos(\theta)\) ทำให้ คาบเท่าเดิม และ แอมพลิจูด = \(\textcolor{red}{|a|}\)
2. มีตัวเลขคูณอยู่ในมุม
\(sin(\textcolor{blue}{b}\,\theta)\)
อันนี้อาจจะมองยากนิดนึง อาจจะมองแบบนี้เพื่อให้ง่ายขึ้นต่อความเข้าใจ สมมติ เรามี \(sin(2\,\theta)\) Input ของฟังก์ชัน sin คือ มุม 2\(\theta\) ดังนั้นกราฟมันจะวนไปเป็นรูปแบบเดิมเมื่อ ครบหนึ่งรอบวงกลม ซึ่งการคูณด้วย 2 ไปที่มุม จะทำให้มุมเดินหน้าเร็วขึ้น 2 เท่า หมายความว่า กราฟก็จะวนซ้ำเร็วขึ้น ด้วยเช่นกัน
เมื่อเรารู้แล้วว่าอะไรเปลี่ยน งั้นลองดูภาพด้านล่างกันครับ

การคูณด้วย 2 ไปที่มุม ทำให้กราฟครบรอบเร็วขึ้นไปอีก 2 เท่าตัว ลองนึกดูว่าถ้าปกติ \(\theta\) เฉยๆ กราฟจะครบรอบมุม \(\theta\) ต้องเดินทางตั้งแต่ มุม 0 ไปถึง 360 องศาแหนะ ถูกมั้ย แต่ถ้ามีเลข 2 มาช่วย \(\theta\) เดินทางจากแค่ 0 ไปถึง 180 องศา เมื่อ นำ 2 ไปคูณกับ 180 องศา จะสังเกตว่า เท่ากับ 360 องศาพอดี ดังนั้น แปลความได้ว่า แค่ \(\theta = \) 180 องศา \((\pi)\) แต่เมื่อมีเลข 2 มาช่วย ก็ทำให้ครบ 1 รอบวงกลมได้ (360 องศา)
คาบของ \(2\,sin(\theta)\) จึงเท่ากับ \(\pi\)
ลองสังเกตดูครับน้องว่า ค่า \(b\) ใน \(b\,\theta\) ยิ่งมากเท่าไหร่ ก็เป็นการช่วย \(\theta\) ให้ครบรอบเร็วขึ้นเท่านั้น ดังนั้น \(b\) มาก คาบก็จะน้อย (วนเร็วขึ้น) เป็นความสัมพันธ์แบบ แปรผกผัน ดังนั้น จากปกติที่เป็น \(sin(\theta)\) หรือ \(cos(\theta)\) เฉยๆ ซึ่งคาบ = \(2\pi\) เมื่อเรานำ \(b\) ไปคูณมุม ก็จะสรุปได้ดังนี้...
กราฟ \(\,sin(\textcolor{red}{b}\,\theta)\) กับ \(\,cos(\textcolor{red}{b}\,\theta)\) ทำให้ คาบเปลี่ยนเป็น \(\dfrac{2\pi}{\textcolor{red}{|b|}}\) แต่ แอมพลิจูดเท่าเดิม
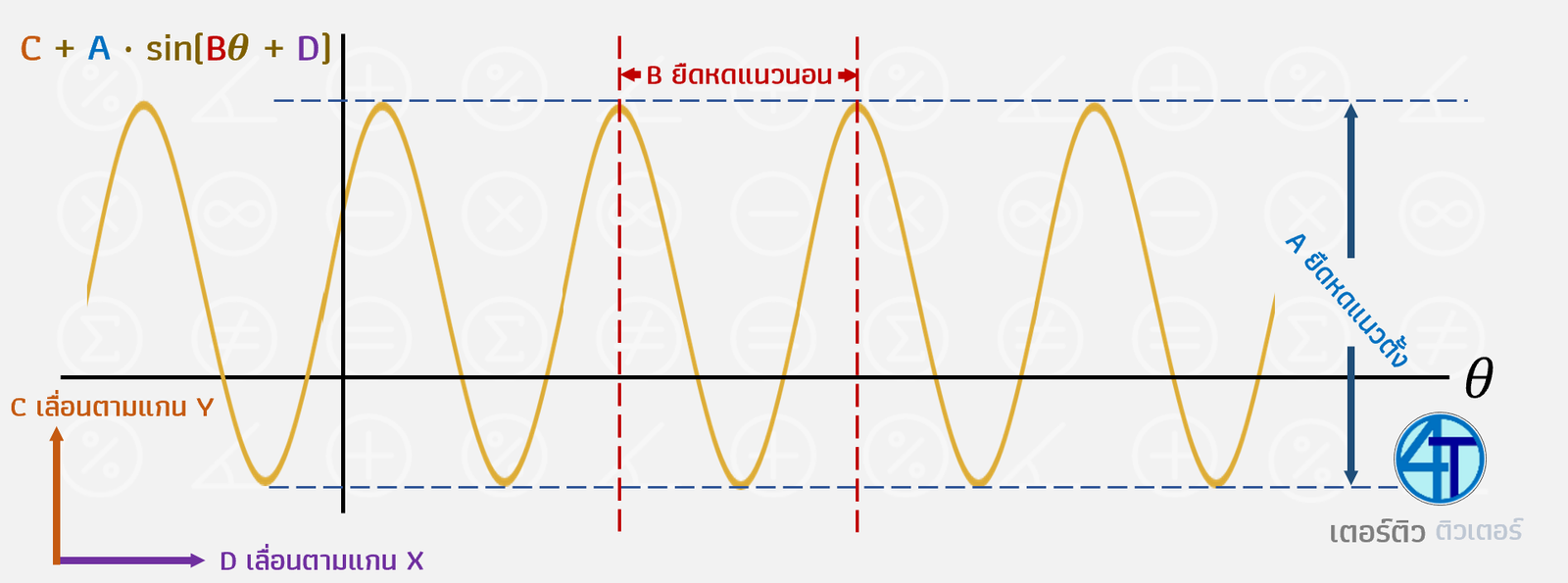
กราฟ tan cot sec และ cosec
พี่ขออนุญาตแปะอีกรอบให้น้องสังเกตกราฟกันดู รูปร่างมันจะแปลกๆ จาก sin กับ cos แต่พี่อยากให้น้องสังเกตอะไรบางอย่างในกราฟกันครับ
ขอบคุณ MathWarehouse สำหรับโปรแกรม Interactive
1. tan กับ cot
สองกราฟนี้จะมีความคล้ายคลึงกันก็ คือ ไหลจากค่า \(-\infty\) ไปจนถึง \(\infty\) ถ้าสังเกตจาก \(tan(\theta)\) เรารู้ว่า \(tan=\dfrac{sin}{cos}\) ดังนั้น \(tan(0)=0\) เพราะ \(sin(0)=0\) (ตัวเศษ) ดังนั้นหากน้องลองเปิดกราฟ \(tan\) ข้างบนไปพร้อมกัน จะสังเกตว่า จุดเริ่มมันเริ่มที่ 0 แต่เมื่อมุมถึง 90 องศา หรือ \(\dfrac{\pi}{2}\) ค่า tan ลู่เข้า \(\infty\) เพราะ? เพราะว่า ค่า \(cos(\dfrac{\pi}{2})=0\) นั่นเองครับ อะไรหารด้วย 0 ก็คือ ไม่นิยาม
ที่น่าสังเกตอีกอย่างก็คือเรนจ์ครับ สังเกตว่ามันเป็นได้ตั้งแต่ \((-\infty, \infty)\) เลยตามที่เราได้ศึกษากันไปในพาร์ทที่แล้ว เรื่องโดเมนเรนจ์ของตรีโกณมิติ
หากพูดถึง คาบ \(tan\) กับ \(cot\) จะให้ผลลัพธ์ตั้งแต่ \((-\infty, \infty)\) และวนไปเรื่อยๆ \((-\infty, \infty)\) \((-\infty, \infty)\) \((-\infty, \infty)\) ... ดังนั้นสิ่งที่น้องต้องรู้คือ ช่วง \((-\infty, \infty)\) มันใช้เวลาเท่าไหร่ (ช่วงมุมแค่ไหน)
2. sec กับ cosec
กราฟทั้งสองจะเป็นโค้งคว่ำหงายสลับกันไปมาเรื่อยๆ สิ่งที่น่าสังเกตคือ จุดเริ่มต้นคือส่วนโค้ง (จุดยอด) ครับน้อง ๆ สังเกตกันดูว่า มันจะเริ่มที่ 1 (ไปถึง \(\infty\)) หรือ -1 (ไปถึง \(-\infty\)) ดังนั้น ก็ตรงตามเรนจ์ที่เราเคยพูดกันไว้ว่า ค่ามันจะเป็นได้ทุกเลข ยกเว้น (-1, 1) นั่นเอง
พี่ครับแล้ว แอมพลิจูด ของ tan cot sec cosec หล่ะครับ ผมจำได้ว่ามันคือ ค่าสูงสุด - ต่ำสุด ทั้งหมดหารด้วย 2 งั้นพี่ขอถามว่า สูงสุดคือ \(\infty\) ถูกมั้ยครับ และต่ำสุดคือ \(-\infty\) ซึ่งมันก็คือไม่จำกัด (เยอะมากๆ) คำตอบคือ แอมพลิจูด เลยไม่มีครับ (ก็คือเค้าไม่คิดกันอะน้อง เพราะมันหาระยะการแกว่งไม่ได้ มันแกว่งเต็มหน้ากราฟขนาดนั้น)
หากบทความพี่เป็นประโยชน์ ฝากแชร์ต่อให้เพื่อนๆ ด้วยนะครับ :')
