เลือกอ่านตามหัวข้อ?

เข้าหาบทความพี่ง่ายๆ จาก Google


โดเมน และ เรนจ์ (Domain \(D_f\) and Range \(R_f\))

ทวนความรู้พื้นฐานกันในเรื่องฟังก์ชันกันก่อนว่า หากเรามี \(y=f(x)=x^2+2\) ค่า \(y\) ที่เป็นไปได้ทั้งหมด ไม่ว่าจะใส่ค่า \(x\) เป็นอะไรก็ตาม เราจะเรียกว่า เรนจ์ของฟังก์ชัน ส่วนค่า \(x\) ที่เป็นไปได้ทั้งหมด เราจะเรียกว่า โดเมนของฟังก์ชัน ซึ่งในเรื่อง ตรีโกณมิติ ฟังก์ชันของเราก็คือ \(y=cot(x)\) (ตัวอย่าง)
ก่อนเข้าเรื่อง การหาโดเมนและเรนจ์ ของฟังก์ชัน ตรีโกณมิติ พี่ขอยกตัวอย่างง่ายๆ เพื่อทวนความรู้น้องๆ กันซักหน่อยครับ สมมติเรามี \(y=\sqrt{x+2}\) จงหาโดเมนและเรนจ์ของฟังก์ชันนี้
เริ่มที่ \(x\) จากโจทย์เราไม่สามารถใส่ค่า \(x\) เป็นจำนวนจริง (\(\mathbb{R}\)) อะไรก็ได้เนื่องจาก ใต้รูทห้ามติดลบ ดังนั้นแปลว่า \(x+2\geq 0\) แก้อสมการจะได้ \(x\geq -2\) ดังนั้น สรุปได้เลยครับว่า \(D_f=[-2,\infty)\)
ส่วนค่า เรนจ์ เนื่องด้วยเราสามารถใส่ใต้รูทเป็น ค่าที่ไม่ติดลบใดๆ ก็ได้ ดังนั้น \(y\) ก็เป็นได้ทุกค่าที่เป็นจำนวนบวกเลย (ถอดรูทออกมาไม่มีทางติดลบ) ฉะนั้น \(R_f=[0,\infty)\)
(1) หาโดเมนก่อน
(2) แล้วค่อยหาเรนจ์จากโดเมน
พี่อยากให้น้องๆ จำให้ขึ้นใจเลยว่า การหาโดเมนนั้นต้องเป็นสิ่งแรกที่น้องเริ่มทำก่อนเสมอ เพราะมันคือ ค่า \(x\) ที่เราสามารถเลือกอะไรมาก็ได้มาใส่ โดยมีสองกรณีที่ต้องระวัง 1) ใต้รูทห้ามติดลบ และ 2) ส่วนห้ามเป็นศูนย์
เรื่องโดเมนกับเรนจ์ หากใครพื้นฐานไม่แม่นแนะนำให้ไปทวนได้ในเรื่อง ฟังก์ชัน ส่วนในเรื่องตรีโกณมิติเราจะแค่เกริ่นกันคร่าวๆ ว่า โดเมนและเรนจ์ของฟังก์ชัน sin cos tan cot sec cosec คืออะไร
อาจสับสน...
หากน้องๆ สับสนระหว่างตัวแปร x, y ที่เป็นตัวบ่งบอกโดเมนกับเรนจ์ กับตัวแปร x, y ที่เป็นค่าคู่พิกัดในวงกลมหนึ่งหน่วย ให้ลองดูเพิ่มเติมในวิดีโอสอนที่ด้านบนเพิ่มเติมนะครับ

โดเมนของ sin และ cos
โดเมนคือค่า x ที่เราใส่ หากเรามองฟังก์ชันตรีโกณมิติเป็นแบบนี้ \(y=sin(x)\) น้องจะสังเกตว่า ค่า x คือ มุม นั่นเองครับ
ดังนั้น มันไม่มีข้อจำกัดเลยในการใส่ค่ามุมเพื่อหา sin กับ cos น้องสามารถใส่ค่ามุมอะไรก็ได้ในโลกใบนี้ เช่น มุม 2563 องศา, มุม -412414 องศา สุดท้ายแล้วยังไงก็มีค่าออกมาได้แน่นอน ดังนั้น โดเมนของทั้ง sin และ cos ก็คือ จำนวนจริงใดๆ (\(\mathbb{R}\))
\(D_{sin}=D_{cos}=\mathbb{R}\)
โดเมนของ cot และ cosec
เนื่องจาก cot เป็นส่วนกลับของ tan ดังนั้น \(cot(x)=\dfrac{1}{tan(x)}\) ซึ่งจากความรู้ม.ต้นที่เราเรียนกันมาว่า \(tan(x)=\dfrac{sin(x)}{cos(x)}\) ทำให้เราได้สมการของ \(cot(x)\) ดังนี้ครับ \(cot(x)=\dfrac{cos(x)}{sin(x)}\)
จำกันได้หรือเปล่าเอ่ยว่า เราสามารถใส่ค่า \(x\) เป็นอะไรก็ได้ ยกเว้นกรณีที่ทำให้ส่วนเป็นศูนย์ (ข้อนี้เรามี) และ ใต้รูทติดลบ (ข้อนี้เราไม่มี) ดังนั้น \(x\) จะเป็นอะไรก็ได้ที่ ตัวส่วน หรือ \(sin(x)\neq 0\)
นึกภาพวงกลม 1 หน่วยตามครับ cos x sin y ดังนั้นต้องมุมไหนบ้างที่ ค่าคู่พิกัดแกน Y เป็น 0? ตรงมุม \(0\) กับ \(\pi\) ถูกมั้ยเอ่ย และหากคิดดีๆ วงกลมหนึ่งหน่วยสามารถ วนกี่รอบก็ได้ ดังนั้นค่า \(0\) กับ \(\pi\) สามารถวนซ้ำๆ ไปอีกทุกๆ \(2\pi\) (หนึ่งรอบวงกลม) ได้

จากภาพด้านบนทำให้น้องๆ เห็นได้ชัดเลยครับว่า ค่า \(x\) ที่เราจะนำไปใส่ฟังก์ชัน \(cot(x)\) นั้นไม่สามารถเป็น \(0, \pi, 2\pi, 3\pi, 4\pi, \dots\) เพราะค่าพวกนี้ทำให้ตัวส่วน (หรือ sin) เป็น 0 นั่นเอง
\(D_{cot}=\mathbb{R}-\{n\pi|\) เมื่อ n เป็นจำนวนเต็มที่ \(\geq 0\}\)
พี่ขอแถมไปเลยว่า การที่ \(cot(x)=\dfrac{cos(x)}{sin(x)}\) แปลว่ามันมีตัวส่วนเป็น \(sin(x)\) ทำให้มีผลกระทบกับ ค่า โดเมนของเรา ถูกมั้ยเอ่ย อีกฟังก์ชันหนึ่งที่มีส่วนเป็น \(sin(x)\) ด้วยเหมือนกันคือ \(cosec(x)\) นั่นเอง เพราะ cosec กับ sin เป็นส่วนกลับซึ่งกันและกัน \(\left(cosec(x)=\dfrac{1}{sin(x)}\right)\) ดังนั้น โดเมนของ cosec จึงเหมือนกับ cot เลยน้องๆ เพราะว่าตัวส่วนห้ามเป็น 0 (sin ไม่เป็น 0)
\(D_{cosec}=\mathbb{R}-\{n\pi|\) เมื่อ n เป็นจำนวนเต็มที่ \(\geq 0\}\)
โดเมนของ tan และ sec
ถ้าน้องสังเกตกันดีๆ ทั้ง tan และ sec ทั้งคู่ต่างมีสมการ ที่ หารด้วย \(cos(x)\) เนื่องจาก \(tan(x)=\dfrac{sin(x)}{cos(x)}\) และ \(sec(x)=\dfrac{1}{cos(x)}\)
ดังนั้น ตามเดิมคือส่วนห้ามเป็น 0 หมายความว่า \(cos(x)\neq 0\) ซึ่งหากน้องๆ นึกถึงวงกลมหนึ่งหน่วยกันแล้วหล่ะก็ น้องจะได้ว่า cos คือค่า x และตรงที่ x มีค่าเป็น 0 คือมุม \(\dfrac{\pi}{2}\) กับ \(\dfrac{3\pi}{2}\) เมื่อเราวนกี่รอบวงกลมก็ได้ น้องก็ต้อง \(+2n\pi\) โดยที่ \(n\geq 0\)
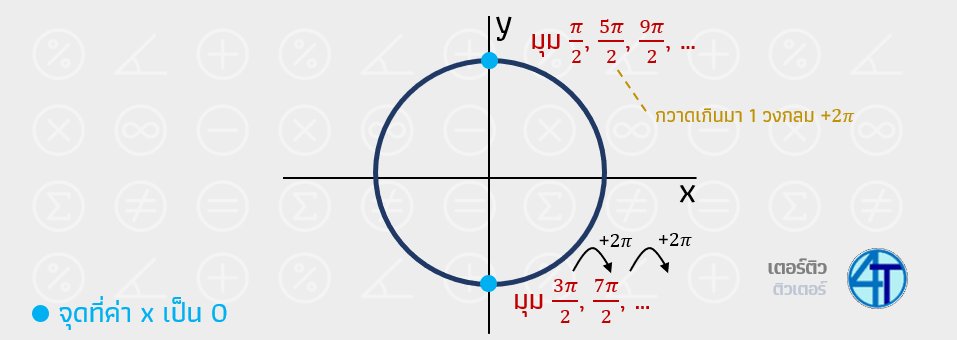
ดังนั้น มุมพวกนี้ \(\dfrac{\pi}{2}, \dfrac{3\pi}{2}, \dfrac{5\pi}{2}, \dfrac{7\pi}{2}, \dots\) เราใช้ไม่ได้เนื่องจาก cos มีค่าเป็น 0
\(D_{tan}=D_{sec}=\mathbb{R}-\left\{\dfrac{(2n+1)\pi}{2}\right\}\) เมื่อ n เป็นจำนวนเต็มที่ \(\geq 0\}\)

เรนจ์ของ sin และ cos
จำกันได้หรือเปล่าเอ่ยว่า "เรนจ์" คือค่า ผลลัพธ์ของฟังก์ชัน \(sin(x)\) และ \(cos(x)\) ซึ่ง x คือมุมที่เราใส่เข้าไป (นึกภาพวงกลมหนึ่งหน่วย) และผลลัพธ์คือค่าคู่พิกัดบน วงกลมหนึ่งหน่วย น้องสามารถสังเกตได้จากภาพด้านล่าง ง่ายๆ เลยครับว่า ค่าของคู่พิกัด x ที่เป็นไปได้ มีแค่ช่วง -1 ถึง 1 เช่นเดียวกันกับค่าคู่พิกัด y ดังนั้น เรนจ์ของ sin กับ cos จึงมีค่าเป็น [-1, 1]
[-1, 1] คือ ช่วงเปิด -1 ถึงเปิด 1 หมายความว่า เป็นค่าตั้งแต่ -1 (รวม -1 ด้วย) ไปจนถึง 1 (รวม 1 ด้วย) นั่นเอง
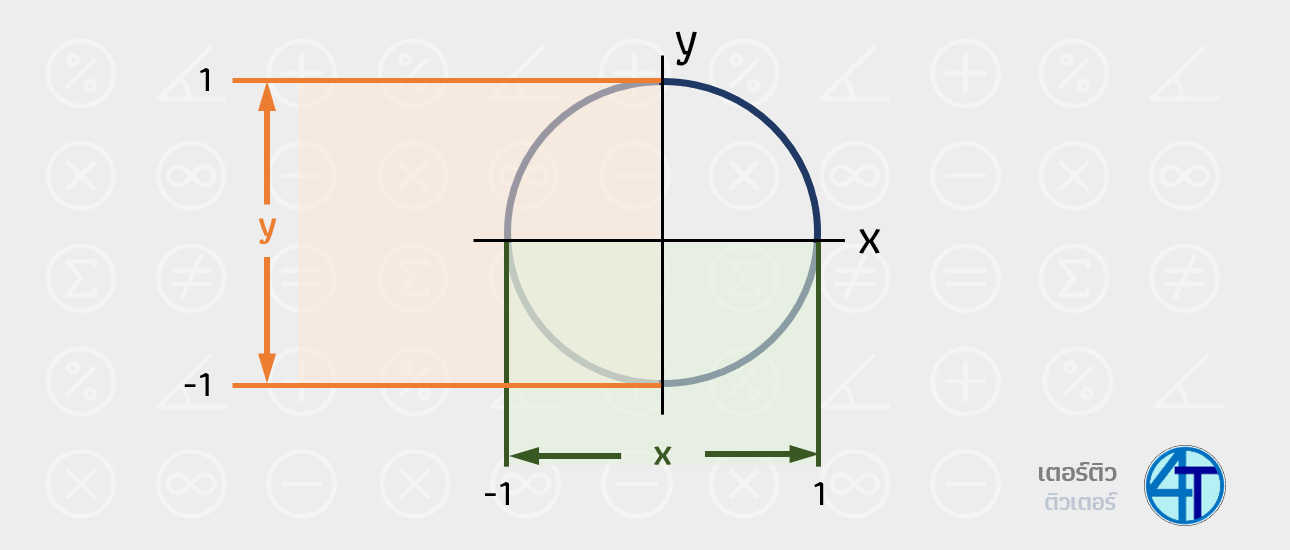
\(R_{sin}=R_{cos}=[-1, 1]\)
เรนจ์ของ tan และ cot
ทวนความจำ tan คือ อะไรส่วนอะไร และ cot คืออะไรส่วนอะไร?
\(tan=\dfrac{sin}{cos}\) ส่วน \(cot=\dfrac{cos}{sin}\) ถูกต้องมั้ยเอ่ย พี่ขอให้น้องมองแค่ tan ก่อน โดยเราจะนึกถึงวงกลม 1 หน่วย เพื่อนรักของเรา (อีกแล้ว 5555) ณ จุดๆ หนึ่งบนวงกลม เราจะมีค่า (x,y) โดยที่ cos x sin y ดังนั้น ถ้าเราพูดถึง \(tan\) ซึ่งคือ \(\dfrac{sin}{cos}\) เราจะได้ว่า มันคือค่า \(\dfrac{y}{x}\) ณ คู่พิกัดใดๆ
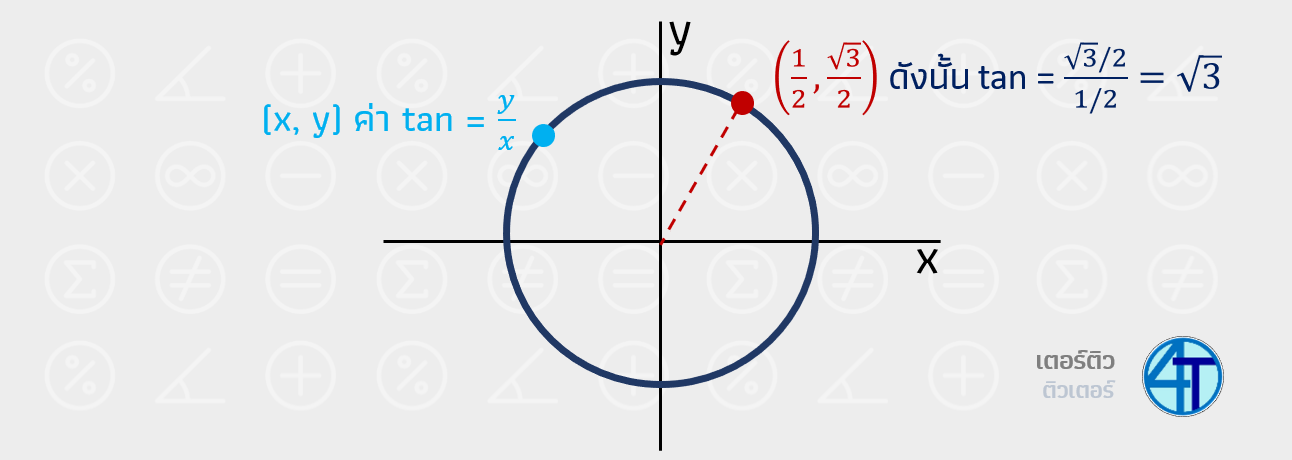
ขอเกริ่นก่อนว่า เรื่องนี้อ่านอาจจะมองเห็นภาพได้ยาก ดังนั้นใครงง ก็ไม่ต้องตกใจนะน้อง ไปดูที่คลิปโลด น่าจะเข้าใจได้ง่ายกว่าตัวอักษร แต่ถ้าใครพร้อมลุยก็จัดไปด้านล่างเลยครับ
การที่เราจะหาเรนจ์ได้ เราก็ต้องลองดูก่อนว่า แต่ละจุดบนวงกลม 1 หน่วย ค่า x กับ y เป็นอะไร เพื่อนำไปสู่ค่า \(tan=\dfrac{y}{x}\) หากน้องสังเกตจากภาพด้านล่าง เริ่มกันที่มุม 0 องศา และกวาดขึ้นไป เราจะได้ว่า เราเริ่มจากคู่พิกัด (1,0) ค่อยๆ เพิ่มค่า y และลดค่า x จนไปถึงคู่พิกัด (0, 1) ที่มุม 90 องศา (ลูกศรสีม่วง)
กลับไปที่การหารเลขปกติ การที่น้องๆ เพิ่มตัวเศษ และลดตัวส่วน ค่าของเศษส่วนนี้ มันจะ เพิ่มขึ้น ถ้าใครงง ให้ลองนึกว่า ตอนแรกน้องมี ของอยู่ y ชิ้น แบ่งให้เพื่อน x คน แต่พอเวลาผ่านไป ของเพิ่มขึ้น (y เพิ่ม) และ เพื่อนลดลง (x ลด) ของที่น้องแบ่งกันกับเพื่อน ก็ต้องได้กันคนละ เยอะขึ้นเรื่อยๆ ถูกมั้ย เพราะของเพิ่มแต่เพื่อนดันน้อยลง (ชีวิตเศร้า เพื่อนหาย TT)

ดังนั้น เราจึงได้ข้อสรุปว่า tan จากมุม 0 องศานะ มันคือ \(\dfrac{0}{1}=\) 0 จะ เพิ่มขึ้นเรื่อยๆ ไปจนถึง tan ที่มุม 90 องศา ซึ่งคือ \(\dfrac{1}{0}=\) ตี้ (อินฟีนิตี้) แปลว่า tan เป็นได้ทุกค่าตั้งแต่ \([0, \infty)\)
ยังไม่จบถูกมั้ยครับ เพราะอันนี้เราคิดแค่ จตุภาคที่ 1 เอง ในเชิงเดียวกัน ถ้าน้องสังเกตที่จตุภาคที่ 2 จะเห็นว่า จตุภาคที่ 2 มีความเหมือน จตุภาคที่ 1 เลยครับ ต่างกันแค่ ค่า x เป็นลบ ดังนั้น สมการของ \(tan=\dfrac{y}{x}\) ที่เคยมีในจตุภาคที่ 1 ก็ต้องถูกเปลี่ยนไปเป็น \(tan=\dfrac{y}{-x}=-\dfrac{y}{x}\)
มันก็คือสมการ \(\dfrac{y}{x}\) แหละ แต่! ใส่เครื่องหมายลบตลอดแนว ดังนั้น จตุภาคที่ 1 เราได้ว่าค่า tan เป็น 0 ถึง ตี้ ในจตุภาคที่ 2 เราก็เลยได้ว่า ค่า tan เป็น -0 ถึง -ตี้ แปลว่า tan เป็นได้ทุกค่าตั้งแต่ \((-\infty, 0]\)
อ่าวพี่ ถ้าผมลองจับ สิ่งที่ไฮไลท์ มารวมกัน? ใช่แล้วน้อง หากเรานำมารวมกัน มันจะได้ว่า tan เป็นได้ทุกค่าตั้งแต่ \((-\infty, 0] \cup [0, \infty)\) กล่าวง่ายๆ คือ \(\mathbb{R}\) (จำนวนจริง) นั่นเอง
\(R_{tan}=R_{cot}=\mathbb{R}\)
พี่ทำไมพี่สรุปของ cot ไปด้วยหละครับข้างบน? น้องสังเกตอะไรมั้ยครับ cot เป็นส่วนกลับของ tan กล่าวง่ายๆ คือ \(cot=\dfrac{1}{tan}=\dfrac{1}{\mathbb{R}}\) ดังนั้น tan เป็นอะไรก็ได้ cot ก็เช่นกันครับ เช่น หากน้องอยากได้ค่า cot เท่ากับ 4.567 มันก็เป็นไปได้ตอนที่ tan คือ 1/4.567 (ซึ่งเราบอกไปแล้วว่าเป็นไปได้ เนื่องจาก 1/4.567 \(\in \mathbb{R}\) ซึ่งเป็นเรนจ์ของ tan)
เรนจ์ของ sec และ cosec
sec คือ ส่วนกลับของ cos และ cosec คือส่วนกลับของ sin ซึ่งเรารู้แล้วจากตอนแรกเลยว่า เรนจ์ของ sin และ cos คือ [-1, 1] ดังนั้นเราจะใช้ความรู้อันนี้แหละน้อง มาช่วยหาว่า เรนจ์ของ sec กับ cosec จะเป็นอะไร
ให้น้องจินตนาการตาม ดังนี้ \(sec=\dfrac{1}{cos}=\dfrac{1}{[-1,1]}\) ลองคิดกันทีละครึ่ง ถ้า cos เป็นบวก \(sec=\dfrac{1}{[0, 1]}\) (เส้นสีม่วง) น้องจะเห็นว่า ค่าของ \(\dfrac{1}{[0,1]}\) เป็นไปได้ตั้งแต่ ตี้ ลงมาถึง 1

อีกฝั่งนึงด้านซ้าย เมื่อ \(sec=\dfrac{1}{[-1, 0]}\) (เส้นสีแดง) ก็คิดคล้ายๆ กันเลย แค่กลับเครื่องหมาย จะได้ว่า เป็นไปได้ตั้งแต่ -1 ถึง -ตี้
จับทั้งสองกรณีมารวมกัน (รวมสิ่งที่เป็นไปได้เข้าด้วยกันทั้งหมด) เราก็จะได้ว่า เรนจ์ของ sec คือ \((-\infty, -1]\cup[1, \infty)\) นั่นเองครับน้องๆ (cosec ก็เช่นกัน เนื่องจาก เรนจ์ของ sin มีค่าเท่ากับ cos)
\(R_{sec}=R_{cosec}=(-\infty, -1]\cup[1, \infty)\)
หากบทความพี่เป็นประโยชน์ ฝากแชร์ต่อให้เพื่อนๆ ด้วยนะครับ :')
