เลือกอ่านตามหัวข้อ?
ทวนกันก่อน กับ ตรีโกณมิติ 3 ตัวที่เหลือ cot sec cosec
ความรู้พื้นฐานตอน ม.3 เลยครับน้องๆ จำกันได้หรือเปล่าว่า cot sec cosec มีความสัมพันธ์อย่างไรกับ sin cos tan? ใช่แล้วครับ มันคือ ส่วนกลับ นั่นเอง
\(cot=\dfrac{1}{tan}\)
\(sec=\dfrac{1}{cos}\)
\(cosec=\dfrac{1}{sin}\)
ใครอยากรู้วิธีจำเดี๋ยวพี่จะแปะวิดีโอไว้ด้านบนบทความนี้ ลองไปฟังกันได้นะครับ มันจะมีทำนองนิดๆ เวลาท่อง sin cos tan cot sec และ cosec และเราจะจับคู่มันดังนี้
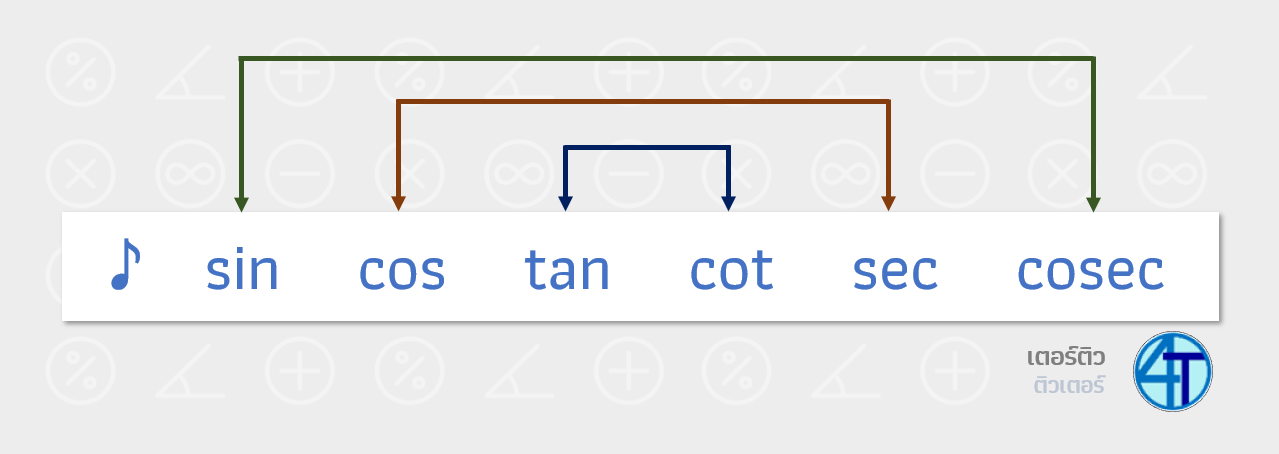
เพราะฉะนั้นหลักการที่พี่อยากให้น้องใช้คือ ไม่ต้องจำสูตรอะไรมากเลย หากเราเจอโจทย์ที่มีค่าของ cot sec cosec (ส่วนกลับของ sin cos tan) ให้เราเปลี่ยนเป็น sin cos tan และใช้หลักการปกติทำแทน หาค่า sin cos tan แบบไม่ต้องจำสูตรให้มากมาย
โคฟังก์ชัน คืออะไร ต้องรู้ ใช้บ่อยมาก!
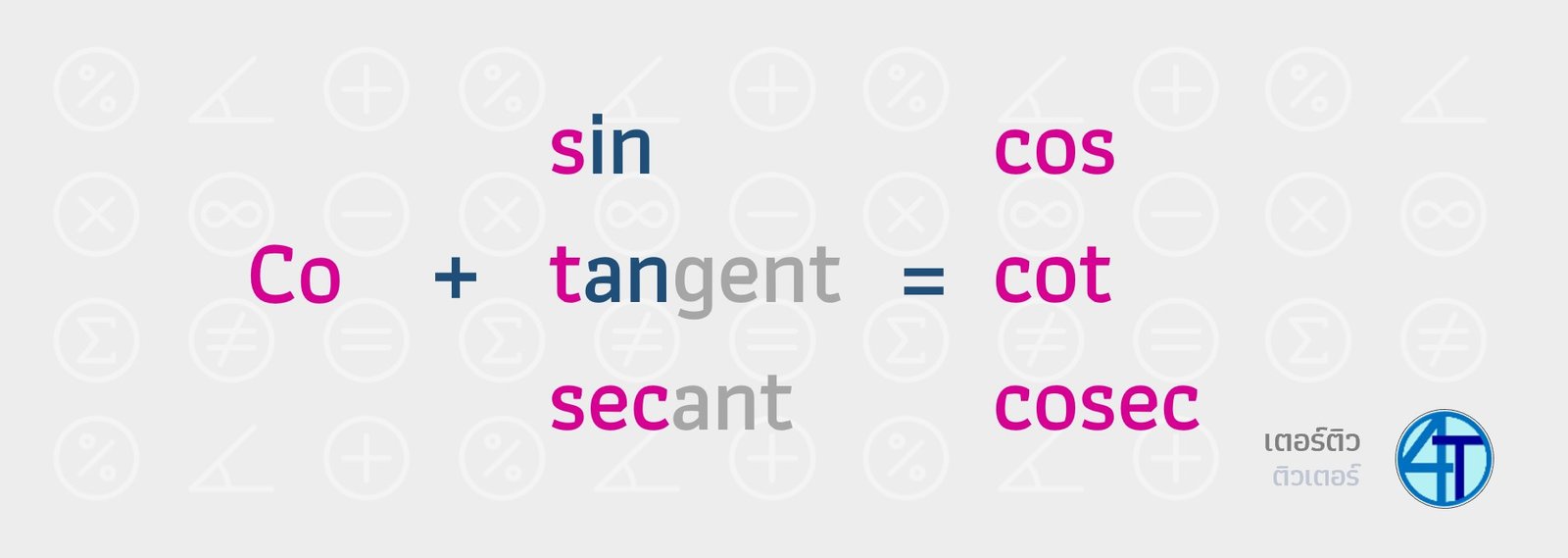
โคฟังก์ชัน เป็นฟังก์ชันคู่กันครับน้อง ๆ ซึ่ง หากถามว่าแล้วในตรีโกณมิติ อะไรคือคู่กันครับพี่? คู่กันในที่นี้คือ มุมประกอบมุมฉาก (Complementary Angle) พูดง่าย ๆ ภาษาคนคือ มุมที่รวมกันเป็น 90 องศานั่นเอง เช่น 60 กับ 30 องศา, หรือ 15 กับ 75 องศา ตั่งต่าง
ดังนั้น ในที่นี้เราจะหมายถึง ฟังก์ชันตรีโกณมิติที่คู่กัน ซึ่งมีค่าเท่ากัน ในมุมที่ประกอบกันได้ 90 องศาพอดี เช่น \(cos(60^\circ)=sin(30^\circ)\) เพราะ 60 กับ 30 องศาเป็นมุมประกอบมุมฉาก (รวมกันได้ 90 องศา) ดังนั้น \(sin\) กับ \(cos\) จึงเป็น โคฟังก์ชันซึ่งกันและกัน เพื่อไม่ให้เป็นการงง เราไปดูกันก่อนว่า 6 ฟังก์ชันในตรีโกณมิติ คู่ไหนเป็น Co Function ของใคร และจากนั้นพี่จะสอนวิธีการใช้ การแปลงต่าง ๆ ว่าเราทำอะไรกับเรื่อง Co Function กันได้บ้าง
\(sin\leftrightarrow{}\textcolor{blue}{co}sin\)
\(tan\leftrightarrow{}\textcolor{blue}{co}tan\)
\(sec\leftrightarrow{}\textcolor{blue}{co}sec\)
วิธีดูหรือจำก็ไม่ยากเลยครับน้อง ๆ โคฟังก์ชัน ก็แค่เติม co- ไปข้างหน้า อย่าง sin เติมไปก็เป็น cosin เราเรียกแค่ 3 ตัวอักษรหน้า ก็ได้เป็น cos ส่วน tan เติมไปก็ cotan เอาแค่ 3 ตัวหน้ามาเรียก ก็จะได้ cot และสุดท้าย sec เติม co เข้าไปก็จะได้ cosec นั่นเอง (ถามว่าแล้วทำไมไม่เอาแค่ 3 ตัวแรกมาเหมือนตัวอื่น ๆ ล่ะครับ? สามตัวแรก จะได้ cos ไงครับน้อง ซึ่งมันซ้ำกับ cos ไปแล้ว เราเลยเรียกชื่อเต็มมันซะเลย)
แล้วมุมไหนที่มันคู่กัน ของ โคฟังก์ชัน ?
จากตอนที่แล้ว ที่เราเรียนหาค่าของ sin cos tan ของมุมใด ๆ โดยใช้หลักการ แกน X เพื่อนบ้าน คราวนี้เราจะทำคล้าย ๆ กันครับน้อง แต่จะใช้ แกน Y เพื่อนบ้าน แทน เป็นยังไงไปดูกัน
หลักการคือ หามุมที่ทำกับแกน Y เพื่อนบ้าน และใช้มุมนั้นแหละ แต่เปลี่ยนเป็น Co Function
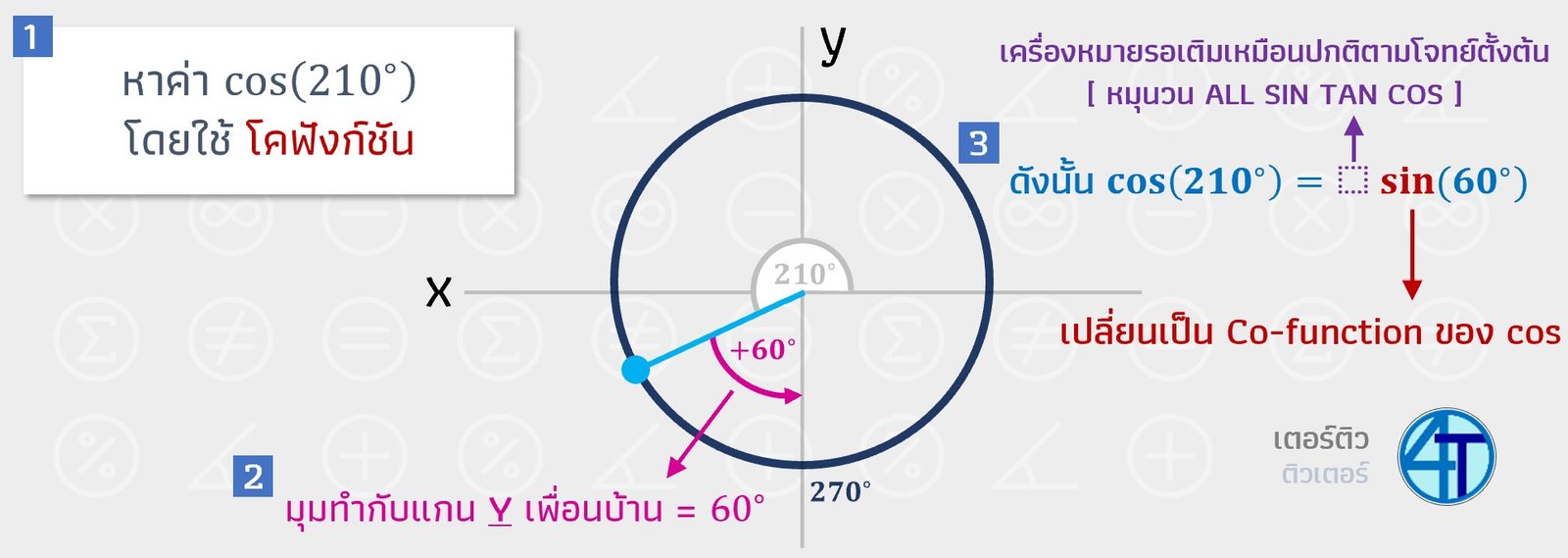
เพื่อความง่าย ให้น้องดูตามสเต็ปจากภาพด้านบนประกอบนะครับ หลักการเปลี่ยนจากตอนที่แล้ว แค่ ใช้แกน Y เพื่อนบ้าน และก็ตอบเป็น Co Function (หากจำกันได้ในตอนที่แล้ว เราจะยังใช้ Function เดิมในการหาคำตอบ เช่น \(sin\rightarrow sin\))
โจทย์ด้านบน คือน้องจะเห็นในกระดาษสูตรกันให้วุ่นวายนั่นเอง ดังนั้น พี่จึงข้อห้ามน้องจำ 55555+ เพราะพี่จะอนุญาตให้น้องจำ สูตรตรีโกณมิติอื่น ๆ ที่พี่จะสอนในบทต่อ ๆ ไปแทนครับ (มันยากกว่า และจำเป็นต้องจำ) น้อง ๆ จะได้ไม่เปลืองพื้นที่ในสมอง น้องจำแค่นี้พอ ตามภาพด้านล่างเลยนะ เลิฟ

หากบทความพี่เป็นประโยชน์ ฝากแชร์ต่อให้เพื่อนๆ ด้วยนะครับ :')
