เลือกอ่านตามหัวข้อ?
เข้าหาบทความพี่ง่ายๆ จาก Google


สัจนิรันดร์ คือ อะไร
สัจนิรันดร์ คือ ประพจน์ที่ เป็นจริงเสมอ หากน้อง ๆ จำได้ในบทความตอนที่แล้ว ที่เรากล่าวถึงในเรื่องของ ตารางค่าความจริง ตารางค่าความจริง เป็นตารางที่เราจะหาค่าความจริงของประพจน์ ในทุกกรณีเลย
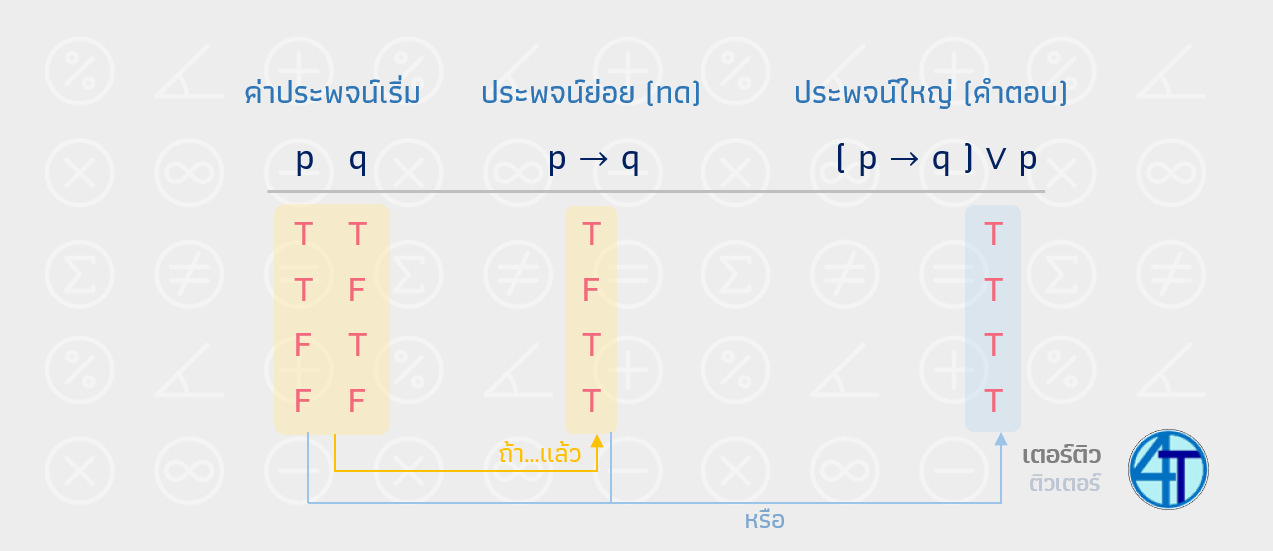
ดังนั้น สัจนิรันดร์ ที่พี่บอกว่าคือ ประพจน์ที่เป็นจริงเสมอ หากน้องสร้างตารางค่าความจริง ทุกแถวจะต้องได้ค่าความจริงเป็นจริงทั้งหมด สมมติว่าเราต้องการหาค่าความจริงของ \((p\to q)\vee p\) ง่ายสุดที่ทำได้ก็คือ สร้างตารางค่าความจริง (4 กรณี เพราะ มี สองตัวแปร \(p\) กับ \(q\)) หากสังเกตจากรูปด้านล่าง น้องจะเห็นว่า ทุกแถวมันเป็นจริงทั้งหมดเลย ดังนั้น เราจึงบอกว่า \((p\to q)\vee p\) เป็นสัจนิรันดร์ เพราะมันเป็นจริงเสมอ
ดังนั้น เราจะไปดูสองวิธีการ การตรวจสอบสัจนิรันดร์ ว่าจะทำยังไงได้บ้าง
การตรวจสอบว่าเป็นสัจนิรันดร์
1. สร้างตารางค่าความจริง
วิธีนี้เป็นวิธีตรงที่น้อง ๆ น่าจะมองเห็นได้ง่าย ว่าทำยังไง เราก็สร้างตารางค่าความจริง ทุกกรณี ขึ้นมา หลังจากนั้น น้องก็ดูเลยว่า ทุกแถวมันเป็นจริงหมดหรือเปล่า ถ้าจริงหมด ก็แสดงว่ามันเป็นสัจนิรันดร์
แต่วิธีนี้มีข้อเสียอย่างร้ายแรงเลยก็คือ ถ้าจำนวนประพจน์ย่อยเราเยอะ ตารางค่าความจริงก็จะใหญ่ขึ้นไปเรื่อย ๆ (2 ประพจน์ 4 แถว, 3 ประพจน์ 8 แถว, 4 ประพจน์ 16 แถว, ... \(n\) ประพจน์ \(2^n\) แถว) ดังนั้น วิธีนี้จึงไม่เหมาะกับการทำข้อสอบ หรือ การหาสัจนิรันดร์ แบบเร็ว ๆ งั้นเราไปดูวิธี 2 กับการ ยัดเยียดความเท็จ กันเลยดีกว่า
2. ยัดเยียดความเท็จ
วิธีนี้เป็นวิธีคลาสสิก ตามชื่อของมันเลยครับน้อง ๆ เราจะทำการยัดเยียดความเท็จให้กับประพจน์ที่เราสนใจ พูดกันง่าย ๆ เลยก็คือ สัจนิรันดร์ คือ ประพจน์ที่เป็นจริงเสมอ ดังนั้น หากเรา ยัดเยียดความเท็จ ให้มันไป แล้วเกิดว่า ทำสำเร็จขึ้นมา (ไม่มีข้อขัดแย้ง) ก็แปลว่าประพจน์นี้ มันเป็นเท็จได้ยังไงล่ะ ดังนั้นมันเลยไม่ใช่สัจนิรันดร์
1. แทนประพจน์เป็นเท็จ
2.1 หากไม่เกิดข้อขัดแย้ง = ไม่ใช่สัจนิรันดร์
2.2 หากขัดแย้ง = สัจนิรันดร์
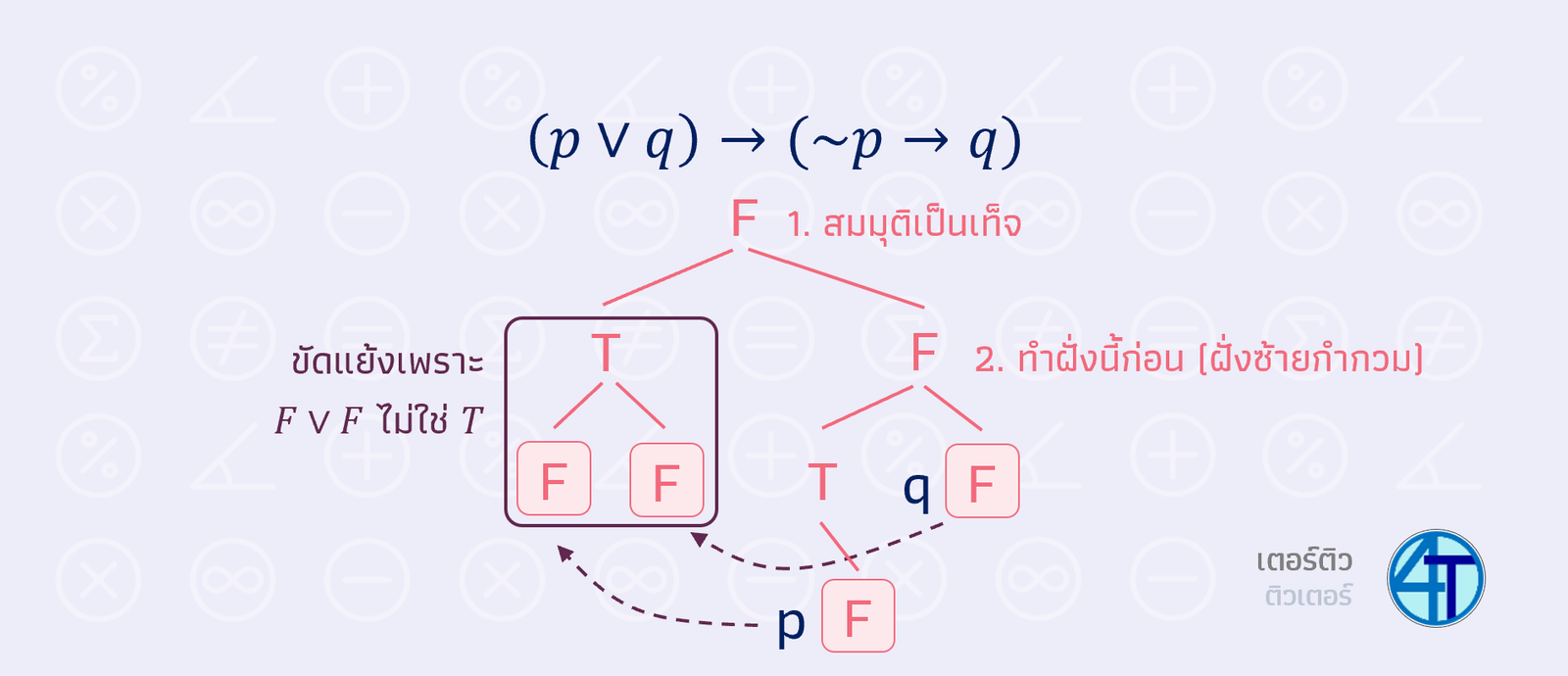
มาดูตัวอย่างเพื่อความเข้าใจง่ายขึ้นกัน สมมติเรามีประพจน์ \((\mathord{\sim}p\wedge q)\to q\) วิธีทำคือเราต้องไล่ย้อนกลับ

1. เราสมมติไปเลยว่าผลลัพธ์เป็นเท็จ ซึ่งการกระทำสุดท้ายที่ทำให้ ประพจน์เป็นเท็จคือ \(\to\) โดย เรานำ \(\mathord{\sim}p\wedge q\) มา \(\to\) กับ \(q\) การที่มันจะเป็นเท็จได้ มีแค่กรณีเดียวเท่านั้น คือ ตัวหน้า จริง ตัวหลัง เท็จ ดังนั้น \(\mathord{\sim}p\wedge q\) เป็นจริง แต่ \(q\) เป็นเท็จ
2. พอเรารู้แล้วว่า \(q\) เป็นเท็จ ให้น้องใส่กรอบให้มันไปเลย เพราะเราเจอค่าความจริง ของประพจน์ย่อยแล้ว
3. ฝั่งซ้าย มี \(q\) อยู่ และเรารู้ค่าความจริง \(q\) แล้ว เราก็โยงมาใส่ ปรากฎว่าเจอกรณีขัดแย้ง เพราะ \(\mathord{\sim}p\wedge q\) ต้องเป็นจริง แต่การที่ \(q\) เป็นเท็จ มันจะทำให้เป็นเท็จทั้งหมด
เมื่อ เจอขัดแย้ง ตอบ ว่ายัดเยียดความเท็จไม่สำเร็จ ดังนั้นเป็นสัจนิรันดร์
อีกสักตัวอย่าง เพื่อความเข้าใจ สมมติเราต้องการเช็คว่า \((p\wedge q)\leftrightarrow (p\vee q)\) เป็นสัจนิรันดร์หรือไม่
ตัวอย่างประพจน์เป็นประพจน์ที่เชื่อมด้วย ก็ต่อเมื่อ ซึ่งหากเรายัดเยียดความเท็จเข้าไป มันจะยังมี สองกรณี ให้เราเลือก (ไม่แน่นอน)
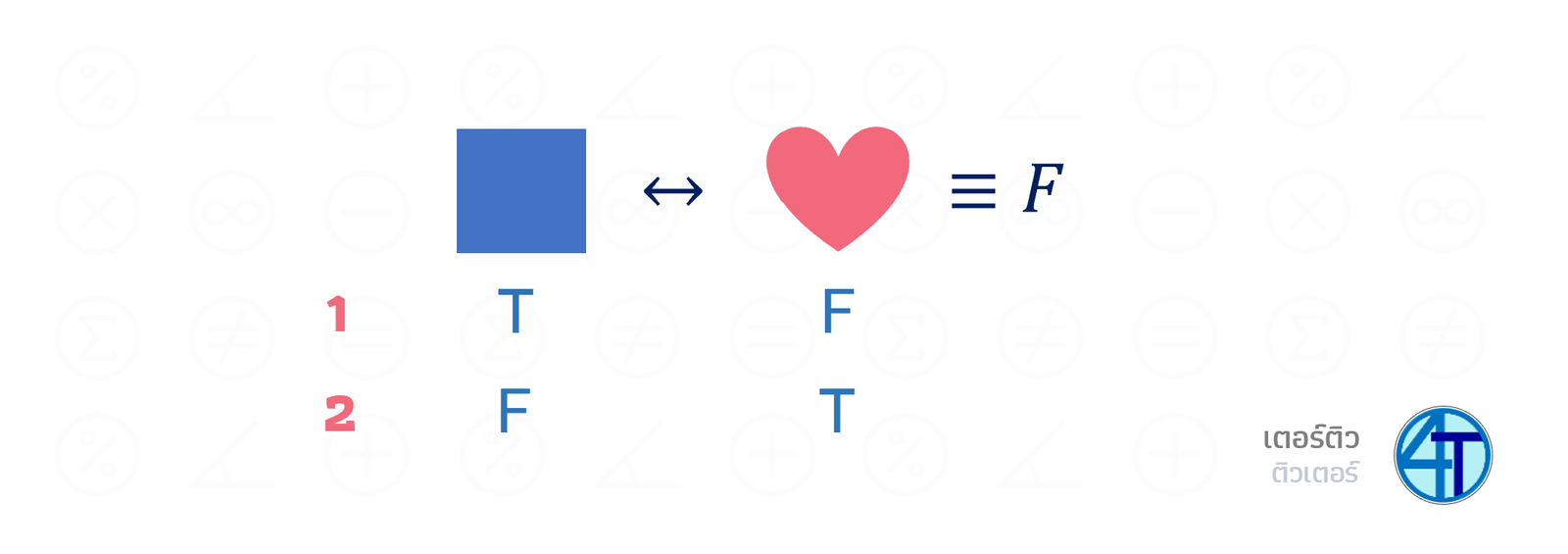
กรณีแรก คือ ซ้ายจริง ขวาเท็จ กรณีสอง คือ ซ้ายเท็จ ขวาจริง
ดังนั้น เราต้องทำทั้งสองกรณี เพื่อเช็คว่า ทุกกรณีขัดแย้งหมด = สัจนิรันดร์ ตรงนี้เป็นข้อควรระวังเลยว่า การยัดเยียดความเท็จ ถ้ามันเกิดหลายกรณีขึ้นมา เราต้องเช็คทุกกรณี ว่ามีบางกรณีไหนที่ไม่ขัดแย้งหรือเปล่า เพราะถ้ามีไม่ขัดแย้ง ก็จะยัดเยียดความเท็จสำเร็จ = ไม่เป็นสัจนิรันดร์ทันที
ทริคเมื่อเจอ "ก็ต่อเมื่อ"
เมื่อเจอก็ต่อเมื่อในสัจนิรันดร์ เรามีวิธีการ 2 วิธี
(1) เช็คทุกกรณี หาว่ามีกรณีไหนหรือเปล่าที่ไม่ขัดแย้ง ถ้าเจอไม่ขัดแย้ง ตอบว่า ไม่ใช่สัจนิรันดร์
(2) เช็คว่า ประพจน์ ซ้าย-ขวา สมมูล กันหรือเปล่า (แนะนำวิธีนี้เพราะง่ายกว่า)
วิธีการเช็คสมมูลกัน (กรณีเจอ "ก็ต่อเมื่อ") เป็นวิธีที่นิยม เพราะการเช็คสมมูลกันทำ ง่ายกว่าการแบ่งหลาย ๆ กรณี เพื่อยัดเยียดความเท็จ หากเราสังเกตกันดี ๆ ประพจน์ \(\square\leftrightarrow\heartsuit\) จะเป็นสัจนิรันดร์เมื่อ ทั้งสองฝั่ง ค่าความจริงเหมือนกันเสมอ ซึ่งเป็นนิยามของ ความสมมูลนั่นเอง ดังนั้นเราก็แปลงโจทย์เป็น หาว่าประพจน์สองฝั่งสมมูลกันหรือเปล่าก็ได้
(1) ถ้าสมมูล = สัจนิรันดร์
(2) ไม่สมมูล = ไม่ใช่สัจนิรันดร์
ดังนั้นข้อนี้ \((p\wedge q)\leftrightarrow (p\vee q)\) เราจะใช้วิธีเช็คความสมมูล โดย เช็คว่า \(p\wedge q\) สมมูลกับ \(p\vee q\) หรือเปล่า ซึ่งคำตอบก็น่าจะมองง่าย ว่า ไม่สมมูลกัน และ กับ หรือ มันจะไปสมมูลกันได้ยังไง ถูกมั้ย ถ้าจำตารางตัวเชื่อมพื้นฐานได้ \(p\wedge q\) กับ \(p\vee q\) มันไม่เหมือนกันทั้งหมดสักหน่อย ถ้ามันเหมือนกันจริง จะแยกเป็นตัวเชื่อม \(\wedge\) กับ \(\vee\) ทำไม
ดังนั้น \(p\wedge q\not\equiv p\vee q\) แปลว่า \((p\wedge q)\leftrightarrow (p\vee q)\) ไม่ใช่สัจนิรันดร์
ถ้ามีหลายกรณี การยัดเยียดความเท็จจะยากขึ้น
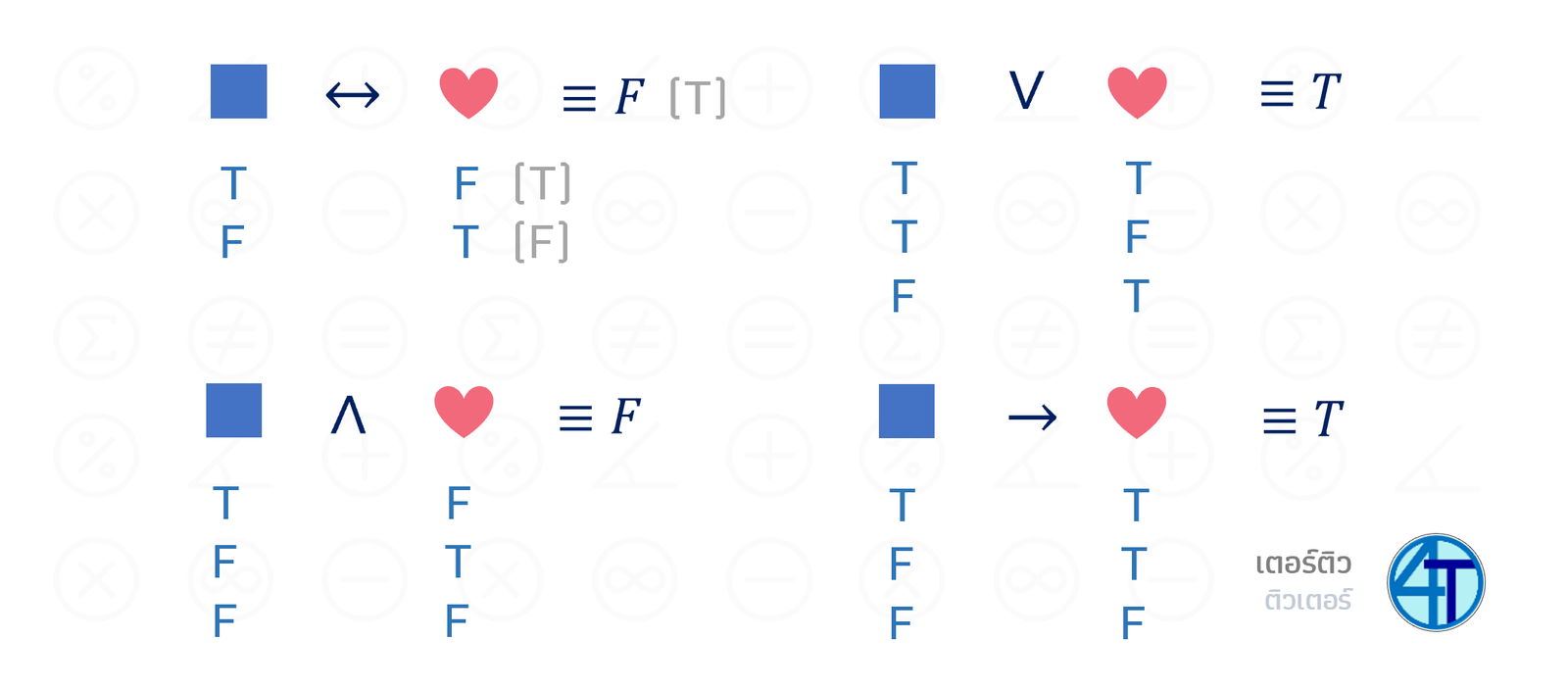
อย่างที่เคยบอกว่า ถ้ามันมีหลายกรณีที่เป็นเท็จ เราต้องเช็คทุกกรณี เผื่อมันมีกรณีไม่ขัดแย้ง ดังนั้น ถ้ามันไม่สามารถจัดรูปได้ หรือสร้างตารางค่าความจริงก็หลายตัวแปรจนไม่อยากสร้าง ก็ต้องทำทุกกรณีอย่างหลีกเลี่ยงไม่ได้
ด้านล่างเป็นประพจน์ตัวอย่างที่สามารถทำให้เกิดหลายกรณีได้ และ หากน้อง ๆ สนใจดูโจทย์เพิ่มเติม สามารถดูวิดีโอที่ด้านบนหน้านี้ได้เลยนะครับ
หากบทความพี่เป็นประโยชน์ ฝากแชร์ต่อให้เพื่อนๆ ด้วยนะครับ :')