เลือกอ่านตามหัวข้อ?
เข้าหาบทความพี่ง่ายๆ จาก Google


ตารางค่าความจริง ของประพจน์ (Truth Table)
ในบทนี้เราจะมาดูการสร้างตารางค่าความจริง หลักการคือ เราอยากรู้ว่าค่าความจริงของประพจน์คืออะไร ใน ทุกกรณีที่เป็นไปได้ หากน้อง ๆ จำได้ เราได้เห็นกันไปบ้างแล้ว ในพาร์ทที่แล้วตรง ตารางค่าความจริง ของตัวเชื่อม \(\vee\;\wedge\;\to\;\leftrightarrow\;\sim\)
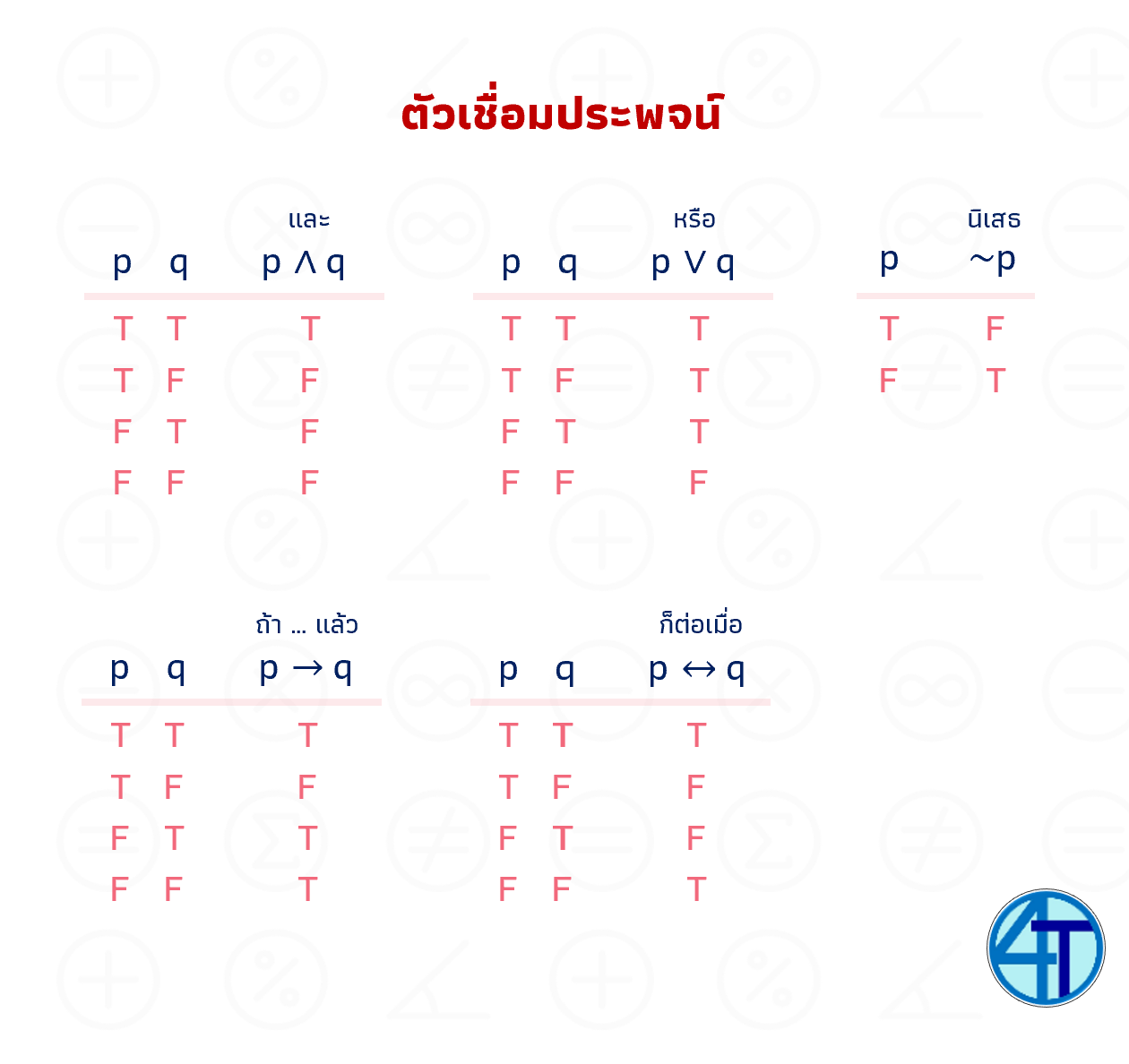
ในพาร์ทนี้เราก็จะสร้างตารางแบบเดียวกัน แต่เป็นของประพจน์ทั่ว ๆ ไป เช่น \((p\to q)\vee q\) เป็นต้น ตารางตัวแปรก็จะใหญ่ แปรผันตรงไปกับความเยอะของประพจน์ ถ้าจำได้ เรารู้แล้วว่า ถ้ามี \(n\) ประพจน์ เราจะได้ตารางขนาด \(2^n\) แถว รูปด้านล่างจะเป็นรูปตารางค่าความจริงที่เราจะสร้างกัน เมื่อมีตัวแปร ตั้งแต่ 1 ตัว (2 แถว) ไปจนถึง 4 ตัว (16 แถว)
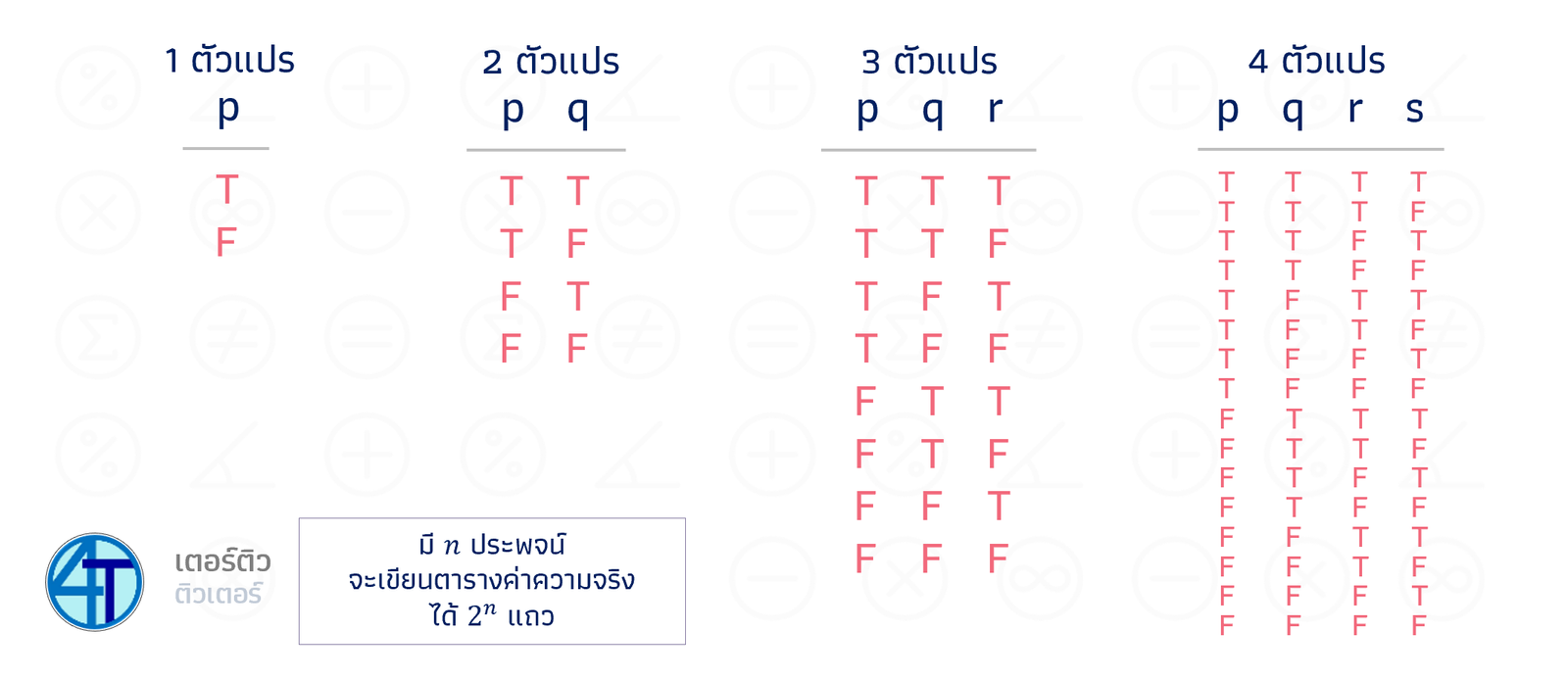
หากใครสนใจเทคนิคการเขียนว่าแต่ละแถวควรเรียงลำดับยังไงให้ไม่พลาดหรืองง สามารถดูเพิ่มเติมที่คลิปประกอบนะครับ
ตัวอย่างการสร้างตารางค่าความจริง เช่น สมมติเรามีประพจน์ \(\mathord{\sim}p\wedge(p\to q)\) เรารู้แล้วว่ามีทั้งหมด 2 ประพจน์ \(p\) กับ \(q\) ดังนั้น เราก็จะสร้างตาราง 4 แถว ที่ประกอบด้วย \(p\) และ \(q\) และในการสร้างค่าความจริง เรามักจะใส่ประพจน์ย่อยลงไปด้วย เพื่อใช้คำนวฯและทดค่าก่อนที่จะได้ ค่าความจริงของประพจน์ใหญ่สุดที่เราต้องการหา
อย่างเช่นในโจทย์ \(\mathord{\sim}p\wedge(p\to q)\) น้องจะเห็นว่า เราต้องคำนวณ ในวงเล็บก่อนซึ่งคือ \(p\to q\) ดังนั้นเราจะเพิ่มคอลัมน์ \(p\to q\) ไปในตารางด้วย และก็ช่อง \(\mathord{\sim}p\) สำหรับประพจน์ \(\mathord{\sim}p\) ตัวหน้า เราจะได้ตารางตามภาพด้านล่าง
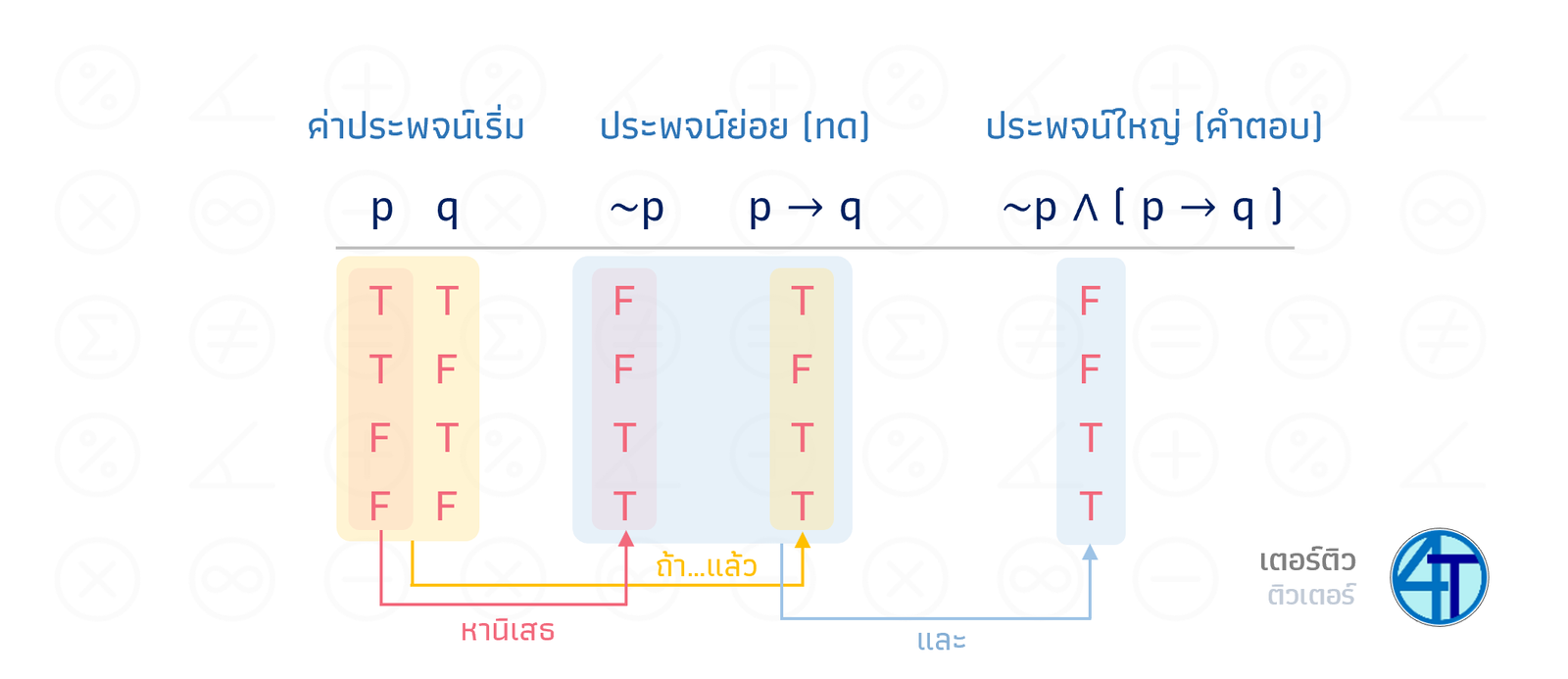
ไอเดียคือค่อย ๆ หยอด จากภาพจะเห็นว่า เราคำนวณประพจน์ย่อยให้เสร็จก่อน \(\mathord{\sim}p\) กับ \(p\to q\) จากนั้นเรานำคำตอบของสองตัวนี้ ไป "และ" กันเพื่อได้คำตอบของประพจน์ \(\mathord{\sim}p \wedge (p\to q)\)
พี่ขอไม่ใส่โจทย์ฝึกในพาร์ทนี้ แต่เดี๋ยวเราไปดูทีเดียวในเรื่องต่อไป สมมูล เพราะเรื่องนี้เราต้องใช้ ตารางค่าความจริงของประพจน์มาช่วยเยอะอยู่แล้ว ดังนั้น เดี๋ยวเราไปฝึกฝนวาดตารางกันในพาร์ท สมมูล ทีเดียวเลย
สมมูล (Equivalent) และ นิเสธ ตรงกันข้าม
หากน้อง ๆ จำได้ที่พี่ขอยืมสัญลักษณ์ของสมมูลมาใช้ก่อน \(\equiv\) และบอกคร่าว ๆ ว่ามันคือความเท่ากัน ให้คิดถึงเครื่องหมายเท่ากับไปก่อน ในพาร์ทนี้เราจะมีดูกันว่า สมมูล คืออะไร
หากเราบอกว่า ประพจน์สองอัน สมมูลกัน มันหมายความว่า ค่าความจริงของสองประพจน์เหมือนกันทุกกรณี ไม่ว่า น้องจะให้ค่าประพจน์ \(p, q, \dots\) เป็นอะไร อาจจะมองอยาก เริ่มที่ตัวอย่างก่อนและกัน
ไอเดียคร่าว ๆ คือ เราก็จะสร้างตารางค่าความจริงของประพจน์ 1 และ 2 ที่น้องตองการเปรียบเทียบ จากนั้นก็เทียบดูว่า แต่ละแถวเหมือนกันหมด หรือไม่
(1) หากเหมือนกันหมด เราเรียกว่าสมมูล
(2) หากต่างกันหมด เราเรียกว่านิเสธ
(3) เหมือนบ้างไม่เหมือนบ้าง ไม่เรียกอะไร
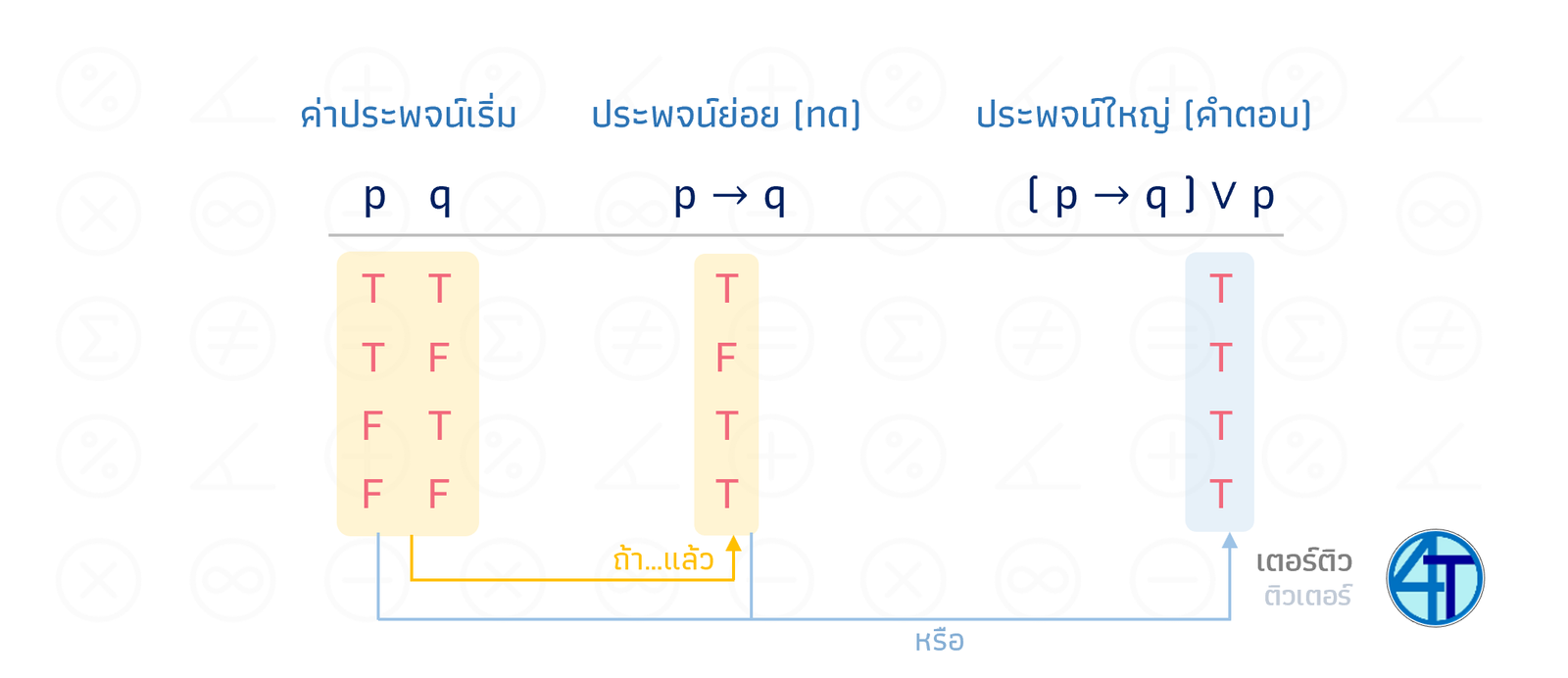
หากน้อง ๆ สังเกตตารางด้านบน เราจะเห็นว่า ประพจน์ \(p\to q\) กับ \(\mathord{\sim}p\vee q\) มีค่าความจริงเหมือนกันหมดทุกกรณีเลย (ทุกแถวค่าความจริงเหมือนกันเป๊ะ) เราเรียกว่า \(p\to q\equiv\mathord{\sim}p\vee q\) (สมมูลกันนั่นเอง)
เท่ากับ
เอาจริง ๆ สมมูลก็คล้าย ๆ เครื่องหมายเท่ากับเลยนะ แต่ใช้กับเรื่องค่าความจริงของประพจน์ เหมือนตัวอย่างข้างบน ที่เราได้ว่า \(p\to q\equiv\mathord{\sim}p\vee q\) ก็หมายความว่า หากน้องเจอ \(p\to q\) เมื่อไหร่ น้องมีสิทธิที่จะเปลี่ยนเป็น \(\mathord{\sim}p\vee q\) ทันที โดยที่ค่าความจริงไม่เพี้ยนแต่อย่างใด
เดี๋ยวในตอนข้างล่างเราจะไปดูกันต่อว่า สมบัติของตัวเชื่อมประพจน์มีอะไร และสามารถใช้งานอะไร และข้อสอบชอบออกอะไรบ้าง
สมบัติ \(T\) \(F\) พื้นฐาน (ต้องเข้าใจแบบไม่จำ)
อันนี้ก็ต่อจากเรื่องความสมมูลของประพจน์นั่นแหละครับน้อง ๆ หากน้องพิจารณาดูดี ๆ จะเห็นว่า พวกสมบัติ มันก็คือสิ่งที่มันเท่ากัน เช่น อย่างใน เรื่องเซต เราก็มีสมบัติ \((A\cup B)'=A'\cap B'\) อะไรประมาณนี้ มันก็คือความเท่ากันของสองฝั่ง ไม่ว่าจะใส่เซต \(A\) หรือ \(B\) เป็นอะไรนั่นเอง ซึ่ง ถ้าพูดในเรื่องของประพจน์ มันก็คือ ประพจน์ ที่สมมูลกัน เพราะค่าความจริงมันเหมือนกันเสมอทุกกรณี
ประพจน์ที่สมมูลกัน กับ สมบัติตัวเชื่อมประพจน์ คือเรื่องเดียวกันนั่นเอง
การทำโจทย์เรื่องตรรกศาสตร์แบบที่น้องจะเจอแบบหนึ่ง คือที่เราจะเขียนกันในเรื่อง ประพจน์ที่สมมูลกัน บทนี่นี่แหละครับ ซึ่งการทำก็มีสองแบบ (1) สร้างตารางค่าความจริง ถ้ามันค่าความจริงตรงกันทุกกรณี ก็ตอบว่า 2 ประพจน์สมมูลกัน แต่วิธีนี้อาจจะช้า หากตัวแปรเยอะ ดังนั้นอีกวิธี (2) ก็คือ การค่อย ๆ ใช้สมบัติความสมมูลแปลง จาก ประพจน์ 1 เป็น ประพจน์ 2 นั่นเอง
หัวข้อนี้ เราจะเริ่มกันแบบพื้นฐานก่อนเลย นั่นก็คือ น้องต้องมองให้ออกว่า แต่ละตัว มีค่าความจริงคืออะไร 3 ตัวหลัก ๆ มีดังนี้

พี่ขอให้น้องลองมองกันทีละตัวนะ และลองดูว่า มันเมคเซ้นต์กับเราหรือเปล่า ถ้าสามตัวบนน้องยังต้องจำเพื่อไปสอบ พี่ขอบอกว่าเป็นการเรียนตรรกศาสตร์ที่ผิด เพราะสามตัวบน น้องควรจะคิดเองได้ ถามตรรกะ ความสมเหตุสมผล ใครสนใจว่า แต่ละตัวมันมาและมีกระบวนการคิดยังไง สามารถกดดูที่คลิปด้านบนหน้านี้ได้เลยนะครับ
สมบัติพื้นฐานประพจน์ (ไม่ต้องท่อง ใช้หลักการเข้าใจ)
1. ตัดตัวซ้ำ
\(p\vee p\equiv p\)
\(p\wedge p\equiv p\)
แบบนี้เป็น กรณีที่สมมุติน้องเจอประพจน์เดียวกัน มากระทำกัน \(p\vee p\) หรือ \(p\wedge p\) เราสามารถตัดทิ้งได้เลย กลายเป็น \(p\vee p\equiv p\) และ \(p\wedge p\equiv p\) จริง ๆ ที่มาก็มาจากตารางค่าความจริงนั่นแหละครับน้อง ๆ หาก \(p\) เป็น \(T\) ไม่ว่าจะเป็น "และ" หรือ "หรือ" ผลลัพธ์ก็ต่างได้ \(T\) หมด ดังนั้นก็คือ \(p\) นั่นเอง ในทางเดียวกัน สำหรับกรณี \(F\) ดังนั้น มันไม่ต้องจำขนาดนั้น แต่ต้องรู้ไว้ เพื่อเอาไว้แก้โจทย์
ที่ต้องระวังก็คือ \(p\to p\not\equiv p\) และ \(p\leftrightarrow p\not\equiv p\) นะ สองตัวเชื่อมนี้ใช้ไม่ได้
2. สมบัติการสลับที่
\(p\vee q\equiv q\vee p\)
\(p\wedge q\equiv q\wedge p\)
\(p\leftrightarrow q\equiv q\leftrightarrow p\)
หากน้อง ๆ จำได้ในเรื่องเซต มันก็ไอเดียเหมือนกัน คือ สมบัติสลับที่สามารถทำได้กับ ทุกตัวเชื่อม ยกเว้น ถ้า...แล้ว กล่าวคือ \(p\vee q\equiv q\vee p\) และ \(p\wedge q\equiv q\wedge p\) และ \(p\leftrightarrow q\equiv q\leftrightarrow p\)
แต่ \(p\to q\not\equiv q\to p\) นะ มองง่าย ๆ ก็เหมือนที่พี่เคยบอกไปว่า "ถ้า...แล้ว" มันคือเหตุและผล ซึ่งเหตุมาก่อน และตามด้วยผล แต่ เราจะไปสลับเหตุและผลไม่ได้นั่นเอง
3. สมบัติการเปลี่ยนกลุ่ม
\((p\vee q)\vee r\equiv p\vee(q\vee r)\)
\((p\wedge q)\wedge r\equiv p\wedge(q\wedge r)\)
\((p\leftrightarrow q)\leftrightarrow r\equiv p\leftrightarrow(q\leftrightarrow r)\)
เหมือนกับข้อ 2 อะไรที่มันสลับที่ได้ ก็ควรจะเปลี่ยนกลุ่มได้
4. สมบัติไม่ไม่ (หักล้างนิเสธ)
\(\mathord{\sim}(\mathord{\sim} p)\equiv p\)
เหมือนในเรื่องคอมพลีเมนต์ของเซต ถ้าเราใส่มันไปสองทีมันก็จะตัดกันทิ้งนั่นเอง
สมบัติพื้นฐานประพจน์ (ต้องจำใช้บ่อย)
1. กระจายนิเสธ
\(\mathord{\sim}(p\vee q)\equiv\,\mathord{\sim} p\;\wedge\mathord{\sim} q\)
\(\mathord{\sim}(p\wedge q)\equiv\,\mathord{\sim} p\;\vee\mathord{\sim} q\)
เหมือนการกระจายคอมพลีเมนต์นั่นแหละน้อง ๆ ดังนั้น กระจายเข้าไปได้ แต่เครื่องหมายต้องกลับด้านหมด
2. สมบัติการแจกแจง
\(p\vee(q\wedge r)\equiv(p\vee q)\wedge(p\vee r)\)
\(p\wedge(q\vee r)\equiv(p\wedge q)\vee(p\wedge r)\)
เหมือนกับเรื่องเซตเป๊ะ ๆ ดังนั้น ใครที่จำได้ อันนี้ก็จะจำได้ไปด้วยเลย
3. สมบัติ \(\to\)
\(p\to q\equiv\,\mathord{\sim} p\vee q\)
\(p\to q\equiv\,\mathord{\sim} q\to\mathord{\sim} p\)
อันนี้ติดดาว ** เลยเพราะ ใช้บ่อยมากถึงมากที่สุดครับ ในเรื่อง ประพจน์ที่สมมูลกัน
4. สมบัติของ \(\leftrightarrow\)
\(\mathord{\sim}(p\leftrightarrow q)\equiv\mathord{\sim}p\leftrightarrow q\equiv p\leftrightarrow\mathord{\sim}q\)
\(p\leftrightarrow q\equiv(p\to q)\wedge(q\to p)\)
อันนี้ออกไม่บ่อยมาก แต่รู้ไว้ก็ดีกว่าไม่รู้ การที่เรามีเครื่องหมาย \(\leftrightarrow\) มันก็เหมือนเป็นลูกศร ชี้ทั้งสองด้านนั่นเอง มันก็เหมือน \(\to\) สองอัน อันแรกคือ p ชี้ q อันสองคือ q ชี้ p ซึ่ง เราก็เลยเขียนเป็นสูตรได้ว่า \(p\leftrightarrow q\equiv(p\to q)\wedge(q\to p)\)
ส่วนโจทย์จะเป็นยังไง มีอะไรออกได้บ้าง เดี๋ยวพี่รวมทุกเนื้อหาไปอยู่ในคลิปทีเดียวเลย หากใครสนใจจิ้มที่วิดีโอด้านบนนะครับ
เยอะจัง จำยังไง?
ส่วนตัวพี่ชอบจำสูตร 3 ที่แปลงจาก "ถ้า...แล้ว" เป็น "หรือ" \(p\to q\equiv\mathord{\sim}p\vee q\) อย่างเดียวเลย ซึ่งใช้บ่อย 90% เลยก็ว่าได้ และก็จำอีกอันคือการกระจาย นิเสธเข้าไป ใน \(\vee\;\wedge\) ซึ่งอันนี้จำไม่ยาก เพราะน้องเรียนกันมาแล้วตั้งแต่เรื่องเซต ดังนั้น พี่แนะนำให้ทำโจทย์ตามลำดับดังนี้ครับ
1. แปลง \(\leftrightarrow\) เป็น \(\to\) ให้หมด
2. แปลง \(\to\) เป็น \(\vee\;\wedge\)
3. โจทย์จะเหลือแต่ \(\vee\;\wedge\) ซึ่งน้องสามารถนำสมบัติที่คุ้นตากันอยู่แล้วมาใช้แก้โจทย์ได้เลย
หากบทความพี่เป็นประโยชน์ ฝากแชร์ต่อให้เพื่อนๆ ด้วยนะครับ :')


