เลือกอ่านตามหัวข้อ?
ฟังก์ชัน vs ความสัมพันธ์

เราจะบอกแบบนี้ก่อนว่า ฟังก์ชัน คือความสัมพันธ์ (เป็นสับเซต) ตามภาพด้านบน แล้วมันหมายความว่าอะไร ? มันหมายความว่า ทุกฟังก์ชันคือความสัมพันธ์ แต่ ไม่ใช่ทุกความสัมพันธ์ที่จะเป็นฟังก์ชัน ดังนั้น
ฟังก์ชัน คือ ความสัมพันธ์ที่มีเงื่อนไข
ก่อนอื่นพี่ขอเขียนความสัมพันธ์ในรูปแบบเป็นภาพก่อน เราจะได้มองกันง่ายขึ้น จำกันได้ใช่ไหมครับน้อง ๆ ว่า \(r=\{(x,y)\in A\times B\}\) เป็นความสัมพันธ์ที่ เราหยิบสมาชิก \(A\) มาเป็นตัวหน้า และสมาชิกในเซต \(B\) มาเป็นตัวหลัง โดยปกติแล้วเราจะเขียนเป็นภาพแบบนี้

ก็คือ มีเซตสองเซต และความสัมพันธ์ก็คือจับตัวหน้ากับตัวหลังเชื่อมกัน (ลูกศร) อย่างที่เห็นด้านซ้าย ความสัมพันธ์ข้างบนมี 2 ลูกศร นั่นแปลว่า \(r_1=\{(1,4), (2,4)\}\) นั่นเอง ซึ่งความสัมพันธ์นี้เป็นฟังก์ชัน
แต่ความสัมพันธ์ด้านขวา \(r_2=\{(1,4),(1,5)\}\) ไม่ใช่ฟังก์ชัน แล้วมันต่างกันอย่างไร ?
ให้น้อง ๆ คิดแบบนี้ครับ ฟังก์ชันเราจะเขียนเป็นสัญลักษณ์ \(f(x)\) เปรียบเสมือนมีเครื่องสมองกลที่ชื่อว่า \(f\) อยู่ น้องได้รับเครื่องนี้มา การใช้งานคือ (1) เครื่องนี้จะรับค่า \(x\) เข้าไป และ (2) คืนค่าเป็นอะไรสักอย่างออกมา (เรียกว่า \(y\) เพื่อความง่าย)
ตัวอย่างเช่น \(f(x)=x^2+5\) แปลว่าเรามีเครื่องสมองกล \(f\) ที่เมื่อรับค่า \(x\) เข้าไป จะคำนวณ \(x^2+5\) คืนค่ากลับมา (\(y\)) ถ้าเราใส่ \(x=1\) ใน \(f(x)\) เราจะได้ว่า \(f(1)=1^2+5=6=y\) นั่นเองครับ
แล้วมันเกี่ยวกับความสัมพันธ์ \(r_1\) และ \(r_2\) ยังไง ? ความสัมพันธ์จะมีคู่อันดับ \((x,y)\) อยู่หลาย ๆ คู่ เช่นใน \(r_1\) เรามี \((1,4)\) และ \((2,4)\)
ตัวหน้า คือ \(x\) สิ่งที่เราใส่เข้าไปในฟังก์ชัน \(f\)
ตัวหลัง คือ \(y\) สิ่งที่ \(f\) คืนค่ากลับออกมา
ดังนั้น ถ้าเราเขียน \(r_1\) ในรูปแบบฟังก์ชัน เราจะได้ว่า \((1,4)\rightarrow f(1)=4\) และ \((2,4)\rightarrow f(2)=4\)
เงื่อนไขของฟังก์ชัน คือ ฟังก์ชันเป็นสมองกลที่ทำงานได้โดยไม่งง พูดภาษาบ้าน ๆ คือ เวลา \(f\) รับค่า \(x\) เข้าไปคำนวณผลแล้ว ผลลัพธ์ที่ออกมา (\(y\)) จะ มีได้แค่ค่าเดียวเท่านั้น ในความสัมพันธ์ \(r_1\) เราได้ \(f(1)=4\) และ \(f(2)=4\) แปลว่า ถ้า \(f\) รับข้อมูลเข้าเป็น \(1\) จะคืนค่า \(4\) กลับออกมา ทำนองเดียวกัน หากรับค่าเข้าเป็น \(2\) จะคืน \(4\) กลับออกมา (สังเกตว่า \(f\) สามารถคืนค่ากลับเป็นตัวเดียวกันได้)
หากลองมาดูที่ \(r_2\) น้อง ๆ จะเห็นว่า \((1,4)\rightarrow f(1)=4\) และ \((1,5)\rightarrow f(1)=5\) หมายความว่า \(f\) เมื่อรับ \(1\) เข้าไปจะคืนค่ากลับมาเป็น \(4\) และ \(5\) อ่าวแล้ว \(f(1)=4\) หรือ \(f(1)=5\) นี่แหละที่เราบอกว่าฟังก์ชันต้องไม่งง นี่มันงงแล้วถูกไหมครับน้อง ๆ เพราะว่าเมื่อเราใส่ \(1\) เข้าไปใน \(f\) ฟังก์ชันจะงงและว่าต้องคืนค่ากลับเป็น \(4\) หรือ \(5\) ดังนั้น \(r_2\) เลยไม่ใช่ฟังก์ชัน
หลักสังเกตฟังก์ชันง่าย ๆ
(1) ตัวหน้า \(x\) ต้องไม่จับคู่กับตัวหลัง \(y\) เกิน \(1\) ตัว
(2) \(f(x)\) ไม่กำกวม มีอย่างมากสุดค่าเดียวเท่านั้น
(3) คู่อันดับในความสัมพันธ์ ถ้าตัวหน้าซ้ำกัน ตัวหลังต้องเหมือนกันเสมอ (ตัวหน้าไม่ซ้ำ)
เป็นฟังก์ชันหรือไม่
\(r_1=\{(1,2),(2,3),(4,3)\}\) เป็นฟังก์ชัน เพราะตัวหน้าไม่ซ้ำกันเลย
\(r_2=\{(1,2),(1,-2),(0,0)\}\) ไม่เป็นฟังก์ชัน เพราะคู่อันดับ \((1,2)\) กับ \((1,-2)\) มีตัวหน้าซ้ำกัน แต่ตัวหลังคนละตัว หมายความว่า \(f(1)=2\) หรือ \(f(1)=-2\) ซึ่งกำกวม ดังนั้นไม่ใช่ฟังก์ชัน
\(r_3=\{(1,2),(3,4),(1,2)\}\) เป็นฟังก์ชัน ถึงแม้ว่าจะมีตัวหน้าเหมือนกันใน \((1,2)\) และ \((1,2)\) แต่ตัวหลังเหมือนกัน ดังนั้น \(f(1)=2\) แน่ ๆ ไม่กำกวม เลยเป็นฟังก์ชัน หรือถ้าคิดอีกแบบก็ได้ครับ สังเกตสัญลักษณ์ เซต ให้ดี ๆ เซตเราจะไม่นับตัวซ้ำ ซึ่ง \((1,2)\) และ \((1,2)\) ถือว่าซ้ำกันเพราะตัวหน้าและตัวหลังเหมือนกันเป๊ะ ๆ แปลว่าเราจะเขียนมันแค่ตัวเดียว ได้ว่า \(r_3=\{(1,2),(3,4)\}\) นั่นเอง ซึ่งตัวหน้าไม่มีซ้ำ ก็เลยเป็นฟังก์ชัน
ข้อสังเกตง่าย ๆ เลยการที่ \(x\) ตัวเดียวกัน จะทำให้ \(y\) มีหลายค่าได้ ส่วนมากก็จะเกิดกับการที่ \(y\)
(1) ติดค่าสัมบูรณ์ หรือ
(2) ยกกำลังคู่
เพราะว่าการยกกำลังคู่ เราสามารถใช้เลขบวกหรือลบมายกกำลังเพื่อเป็นค่าเดิมได้ \(-5^2=5^2=25\) และค่าสัมบูรณ์ เราก็ใช้ค่าบวกและลบได้ทั้งคู่ \(|5|=|-5|=5\) ประมาณนี้ครับ ส่วนมากดูที่ตัว \(y\) ได้เลย เพื่อวิเคราะห์ว่าเป็นฟังก์ชันหรือเปล่า
เป็นฟังก์ชันหรือไม่ โดยการดูกราฟ
หากน้อง ๆ จำได้ เราได้เรียนกันไปแล้วในบท กราฟของความสัมพันธ์ ว่าเราสามารถวาดกราฟออกมาได้ เพราะความสัมพันธ์ก็คือ เซตของคู่อันดับ \((x,y)\) หลาย ๆ ตัวนี่เอง
ในบทนี้ เราจะมาเรียนรู้กันว่า หากเรามีกราฟของความสัมพันธ์ เราจะเช็คจากกราฟได้ยังไงบ้างว่า ความสัมพันธ์นั้น ๆ เป็นฟังก์ชันหรือไม่
หากจำได้ในเงื่อนไขของฟังก์ชัน เรารู้ว่า \(x\) จะต้องไม่ซ้ำ หรือกล่าวง่าย ๆ ว่า จะต้องไม่มี \((x,y_1)\) และ \((x,y_2)\) ในความสัมพันธ์โดยที่ \(y_1\ne y_2\) นั่นเองครับ แล้ว \((x,y_1)\) กับ \((x,y_2)\) มันหน้าตาเป็นยังไงบนกราฟ หน้าตาของมัน จะเป็นแบบในรูปด้านล่าง

พี่เขียนตัวอย่างออกมาเป็นสองกลุ่ม (ชมพู, น้ำเงิน) ให้น้องลองสังเกตแต่ละกลุ่มดูครับ สังเกตว่า ถ้าเรามีจุด \((x,y_1)\) และ \((x,y_2)\) มันจะอยู่ตำแหน่ง \(x\) เดียวกัน ทำให้
เมื่อเราลากเส้นดิ่งพสุธา (แนวตั้ง) มันจะตัดทั้งสองจุด
ดังนั้น เราเลยสรุปได้ง่าย ๆ เลยว่า ถ้ามีกราฟของความสัมพันธ์ให้เรามา แล้ว ถ้าเราสามารถลากเส้นดิ่งพสุธาตรงไหนก็ได้ แล้วมันเกิดตัดกราฟ สองจุด (หรือมากกว่า) แปลว่า ไม่ใช่ฟังก์ชัน
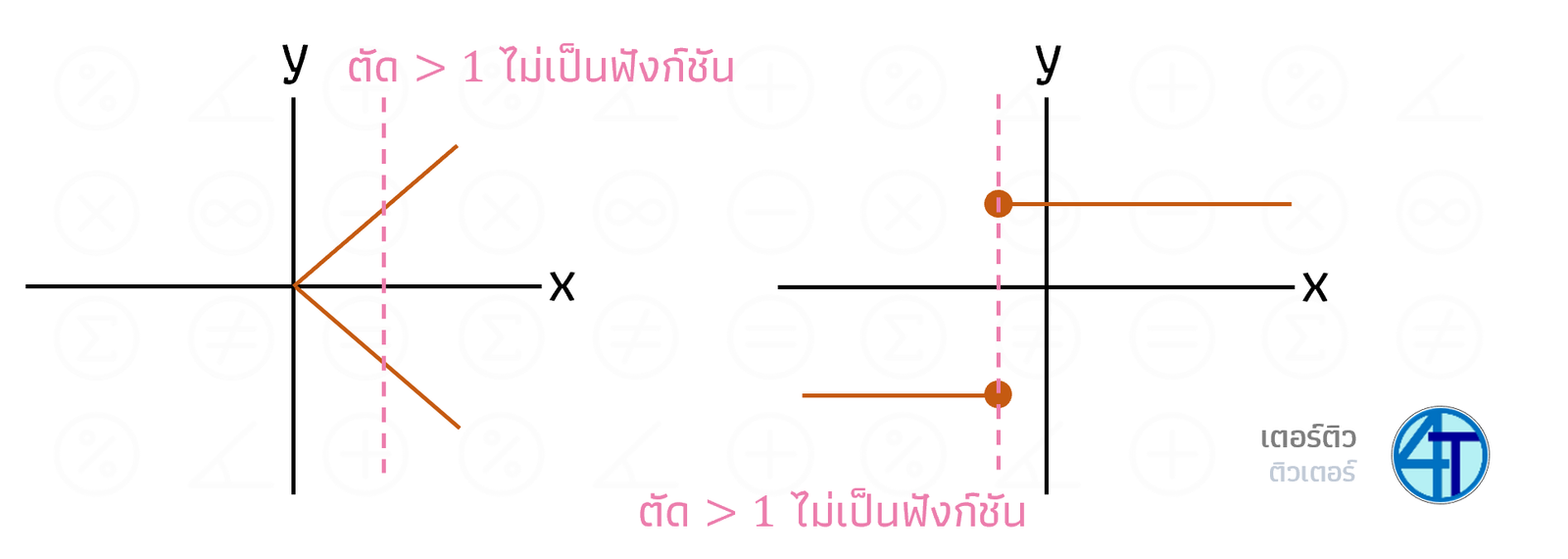
ตัวอย่างแบบที่ไม่เป็นฟังก์ชัน อยากให้ดูตัวอย่างฝั่งขวา เป็นตัวอย่างที่หากเราลากเส้นดิ่งตรงจุดอื่น มันจะตัดกราฟ 1 ที่เสมอ ดังนั้น มันคล้าย ๆ ว่า เป็นฟังก์ชันนะ เพราะไม่ผิดเงื่อนไข แต่ถ้าเราลากตรงจุดรอยต่อ น้อง ๆ จะสังเกตเห็นเลยว่า รอยต่อทั้งบนและล่างนั้นเป็นจุดทึบ แปลว่า เอาจุดตรงนั้นทั้งคู่ ทำให้เวลาเราลากเส้นดิ่งผ่านจุดนั้น จะตัดกราฟ 2 จุด ก็เลยได้ว่าไม่เป็นฟังก์ชัน

ส่วนแบบด้านบนนี้ ก็คือเป็นฟังก์ชัน เพราะไม่ว่าจะลากเส้นดิ่งเส้นไหน ก็ไม่สามารถตัดกราฟเกิน 1 จุดได้เลย
แปลงฟังก์ชันเป็นรูปมาตรฐาน \(f(x)\)
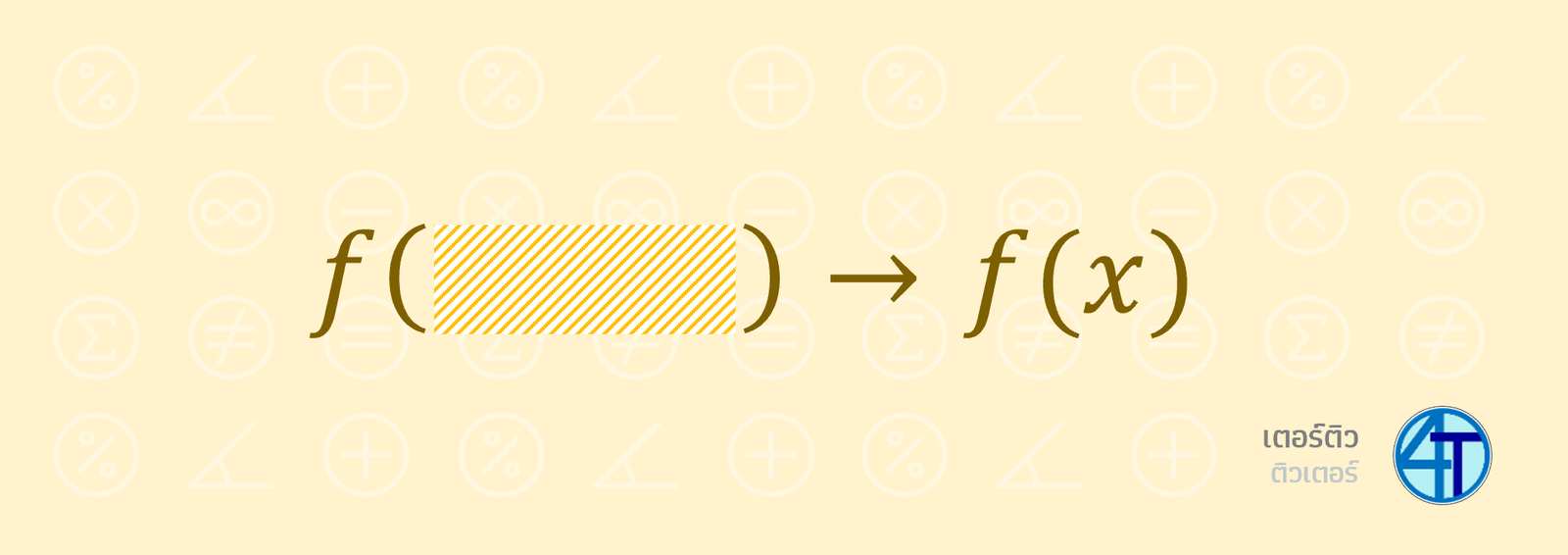
เนื่องจากหากโจทย์ให้ \(f(x)=x^2+2x+5\) มาแบบนี้ โจทย์ถามหา \(f(1)\) เราก็แค่จับแทนเลย \(f(1)=1^2+2(1)+5=8\) แต่โจทย์ส่วนมากจะมีการพลิกแพลงอีกตลบ
เช่น \(f(5+x)=x^2+2x+5\) โจทย์ถามหา \(f(7)\) เราต้องเขียนให้หน้าตาคล้ายโจทย์มากที่สุดก่อน \(f(7)=f(5+\textcolor{blue}{2})=\textcolor{blue}{2}^2+2(\textcolor{blue}{2})+5\) สังเกตว่าเราใช้ \(x=\textcolor{blue}{2}\) เพราะว่า ถึงแม้ข้อนี้จะถามหา \(f(7)\) แต่โจทย์ให้หน้าตาฟังก์ชันเป็น \(f(5+x)\) ดังนั้น แปลว่า \(f(7)=f(5+\textcolor{blue}{2})\sim f(5+\textcolor{blue}{x})\) เราเลยได้ \(x\) เป็น \(2\) นำไปแทนฝั่งขวานั่นเองครับ ซึ่งจะได้ว่า \(f(7)=f(5+\textcolor{blue}{2})=\textcolor{blue}{2}^2+2(\textcolor{blue}{2})+5=13\)
อีกตัวอย่าง \(f(2x+1)=4x+1\) จงหา \(f(5)\) เนื่องจาก สิ่งที่ฟังก์ชันเรารับคือ \(2x+1\) ดังนั้น เราต้องจับแก้สมการก่อน ว่า ถ้า \(5\) คือสิ่งที่เรานำเข้าฟังก์ชัน ซึ่งเท่ากับ \(2x+1\) แล้ว \(x\) จะมีค่าเท่าใด
\(\require{cancel} \begin{aligned} 2x+1&=5\\ x&=2 \end{aligned}\)
ดังนั้น เราได้แล้วว่า \(x=2\) ลองแทนกันดูเลย
\(\require{cancel} \begin{aligned} f(2x+1)&=4x+1\\ f(2\cdot 2+1)&=4(2)+1\\ f(5)&=9 \end{aligned}\)
สังเกตว่ามันต้องแก้สมการหลายตลบ และหากมีต้องหาหลาย ๆ ค่าก็ต้องแก้สมการทุกรอบเลย ซึ่งไม่ค่อยโอเค
ดังนั้น เราจะพยายามแปลงให้อยู่ในรูป \(f(x)\) ที่ใช้งานได้สะดวก
วิธีทำก็คือให้แทนตัวแปรอื่นเข้าไปที่ฟังก์ชันเลย เช่น \(f(5+x)=x^2+2x+5\) เราจะใช้ \(k\) เป็นตัวแปรใหม่ และจุดหมายของเราคือ ได้ฟังก์ชันที่ใช้ได้ง่าย \(f(k)\) เราเลยจะแทนเข้าไปเลยดังภาพด้านล่าง

สังเกตเมื่อเราแทนแบบนี้ เราจะได้สมการ \(5+x=k\) เมื่อเราได้แบบนี้ เราต้องทำการแก้สมการ เพราะตอนนี้ เรามี \(f(k)=x^2+2x+5\) ซึ่งมันคนละตัวแปรกัน เราจะพยายามเปลี่ยน \(x\) เป็น \(k\) ดังนั้น เราต้องแก้สมการ และ เขียน \(x\) ในรูปของ \(k\)
\(\require{cancel} \begin{aligned} 5+x&=k\\ x&=k-5 \end{aligned}\)
ดังนั้นเราจะจับ \(x=k-5\) ไปแทนใน สมการที่เราค้างอยู่เพื่อเปลี่ยนทุกอย่างเป็น \(k\) นั่นเองครับ
\(\require{cancel} \begin{aligned} f(k)&=x^2+2x+5\\ &=\textcolor{blue}{(k-5)}^2+2\textcolor{blue}{(k-5)}+5\\ &=k^2-10k+25+2k-10+5\\ f(k)&=k^2-8k+20 \end{aligned}\)
เนื่องจากฟังก์ชันเวลาเราเขียนตัวแปร \(x\) หรือ \(k\) จริง ๆ มันคือตัวแปรสมมติขึ้นมา แปลว่า เราสามารถเปลี่ยน \(k\) ทุกตัว กลายเป็นตัวแปร \(x\) เหมือนเดิมได้ จึงได้คำตอบสุดท้ายว่า
\(\require{cancel} \begin{aligned} f(x)=x^2-8x+20 \end{aligned}\)
จากตัวอย่างด้านบน ที่เรารู้ว่า \(f(7)=13\) ลองจับเข้าไปแทนในฟังก์ชันตัวใหม่นี้กันดูครับ \(f(\textcolor{blue}{7})=\textcolor{blue}{7}^2-8(\textcolor{blue}{7})+20=13\) จะเห็นว่าคำตอบเหมือนกันเลย เพราะมันเป็นฟังก์ชันเดียวกันที่เราจัดรูปให้ใช้ง่ายขึ้นนั่นเอง
โจทย์บางข้อ อาจจะพลิกแพลงไปอีกระดับคือให้เราแปลง แต่ไม่ได้แปลงเป็น \(f(x)\) เช่น กำหนดให้ \(f(x-1)=2x-1\) ให้หา \(f(x^2)\)
เราต้องการสุดท้ายแล้วเป็น \(x^2\) ดังนั้น เราจะแทนตัวแปรใหม่ \(k^2\)
\(\require{cancel} \begin{aligned} x-1&=k^2\\ x&=k^2+1 \end{aligned}\)
ดังนั้น เมื่อเราจะ \(x\) ในรูปของ \(k\) แล้ว เราก็นำไปแทน
\(\require{cancel} \begin{aligned} f(x-1)=f(k^2)&=2x-1\\ &=2(k^2+1)-1\\ &=2k^2+1 \end{aligned}\)
เราจึงตอบได้เลยว่า \(f(x^2)=2x^2+1\) โดยการเปลี่ยนตัวแปร \(k\) กลับเป็น \(x\)
หากบทความพี่เป็นประโยชน์ ฝากแชร์ต่อให้เพื่อนๆ ด้วยนะครับ :')

