ความสัมพันธ์ และ กราฟของความสัมพันธ์ ม.4

นิยามความสัมพันธ์

ตอนนี้เราจะพูดถึง ความสัมพันธ์ส่วนฟังก์ชันจะพูดในบทต่อ ๆ ไป ครับ บทที่แล้วเราเรียนเรื่องผลคูณคาร์ทีเซียนไปแล้ว ซึ่งเป็นการจับคู่ สมาชิกเซตหน้ากับเซตหลัง เข้าด้วยกัน ทุกคู่ที่เป็นไปได้

สมมติ \(A=\{1,3\}\) และ \(B=\{-1,-3\}\) จะได้ว่า \(A\times B=\{(1,-1),(1,-3),(3,-1),(3,-3)\}\) มีทั้งหมด 4 คู่

ให้น้องจินตนาการว่า แต่ละคู่ คือการจับคู่กัน เหมือนเป็นคนสองคนมาคู่กันก็ได้ ในกรณีนี้ก็คือ มีคู่ทั้งหมด 4 คู่

[1] \((1,-1)\)
[2] \((1,-3)\)
[3] \((3,-1)\)
[4] \((3,-3)\)

ความสัมพันธ์ คือ ข้อตกลงร่วมกัน ว่าการจับคู่ต้องเป็นไปตามนี้นะ เช่น ความสัมพันธ์ ที่มี \((a,b)\) โดยที่ \(a\) กับ \(b\) ต้องเป็นเลขตรงข้ามกัน เช่น \(4\) กับ \(-4\) หรือ \(x\) กับ \(-x\) ประมาณนี้ เราจะเห็นว่า คู่ที่ [2] กับ [3] ไม่เป็นจริงตามเงื่อนไขความสัมพันธ์ เพราะ

คู่ที่ [2] คือ \((1,-3)\) มันไม่ได้เป็นคู่ที่ตัวเลขตรงข้ามกัน

คู่ที่ [3] คือ \((3,-1)\) ก็เหมือนกัน

แต่คู่ที่ [1] กับ [4] ใช่นะ เป็นตัวเลขที่ตรงกันข้ามกัน

ดังนั้น ความสัมพันธ์ ที่ตัวเลขตรงกันข้ามกัน ก็จะตัดบางตัวออกจาก ผลคูณคาร์ทีเซียน นั่นเอง แปลว่า เราจะได้เซตของคู่อันดับที่เล็กลง

สรุปทั้งหมดข้างบน หากน้องเข้าใจไอเดียแล้ว เราจะเจอนิยามว่า

\(r\) คือความสัมพันธ์ ซึ่งถ้ามีเงื่อนไข มันก็คือเราจะตัดบางคู่ออกจากผลคูณคาร์ทีเซียน ดังนั้น \(r\) ก็เลยเล็กลงเสมอ (อาจเท่ากับได้ กรณีที่ทุกคู่เป็นตามเงื่อนไขความสัมพันธ์ทั้งหมด) นี่เลยเป็นที่มาของสัญลักษณ์สับเซต

ตัวอย่างความสัมพันธ์

ตัวอย่างที่ 1 กำหนดให้ \(A=\{2,3\}\) และ \(B=\{4,5\}\) และ \(r\) เป็นความสัมพันธ์ระหว่าง \(A\times B\) โดยที่ ผลรวมได้ \(7\)

ถ้าเราจับคู่ทั้งหมด จะได้ผลคูณคาร์ทีเซียน \(A\times B=\{(2,4),(2,5),(3,4),(3,5)\}\) แต่ความสัมพันธ์ \(r\) ที่เราต้องการคือ "ผลรวมคือเจ็ด" แปลว่า เอาแค่ \((2,5)\) กับ \((3,4)\) แค่สองคู่อันดับ เราจึงตอบว่า \(r=\{(2,5),(3,4)\}\) 

โจทย์แบบนี้ปกติเราจะเจอในรูปแบบคณิตศาสตร์ว่า

ด้านบนเป็นการพูดแบบที่โจทย์ถาม แต่ในเชิงทางการเวลาที่น้องจะเจอในห้องสอบ ดังนั้น เราต้องแปลงไปแปลงกลับ ทำความเข้าใจโจทย์ให้ได้นะ

โจทย์บอก ความสัมพันธ์ \(r\) เป็นความสัมพันธ์บน \(A\times B\) ก็คือ \(A\) ตัวหน้า \(B\) ตัวหลัง โดยมีเงื่อนไขคือ \(x+y=7\) นั่นเอง อยากให้สังเกต \(x\) กับ \(y\) ดี ๆ ครับ เพราะ \(x\) คือสมาชิกจาก \(A\) ส่วน \(y\) คือสมาชิกจาก \(B\) นะ ดูได้จาก \((x,y)\in A\times B\)

ตัวอย่างที่ 2 กำหนดให้ \(A=\{1,2\}\) และ \(B=\{1\}\) จงหาความสัมพันธ์ \(\{(x,y)\in A\times B\;|\;x\le y\}\)

โจทย์ข้อนี้ เราจะไม่เขียนออกมาทั้งหมด แต่เราจะวิเคราะห์โดยโจทย์ถามเราให้หาความสัมพันธ์ของตัวหน้าน้อยกว่าหรือเท่ากับตัวหลัง ซึ่งตัวหน้ามาจาก \(A\) และตัวหลังมาจาก \(B\) ดังนั้น เมื่อเราหยิบตัวอะไรจาก \(A\) มา เราจะหาคู่จาก \(B\) ตามเงื่อนไขเท่านั้น "ตัวขวามากกว่าหรือเท่ากับ"

หยิบ \(1\) จาก \(A\) ตัวแรก เราสามารถเลือกหยิบ \(1\) จาก \(B\) ได้เพราะ \(1\le 1\)

หยิบ \(2\) จาก \(A\) ตัวแรก เราไม่สามารถหยิบอะไรจาก \(B\) ได้เลย เพราะ \(2\not\le 1\)

ดังนั้น แปลว่าเราได้แค่ \(\{(1,1)\}\) เป็นคำตอบของความสัมพันธ์

กราฟของความสัมพันธ์

ในหัวข้อนี้ เราจะสนใจเฉพาะ \((x,y)\) โดยที่ \(x\) กับ \(y\) เป็นตัวเลข เพราะมันมีรูปร่างหน้าตาเหมือนกับ คู่พิกัดบนระนาบ 2 มิตินั่นเองครับ หมายความว่า ถ้าเรานำความสัมพันธ์ไปพล็อตจุดบนกราฟ เราสามารถทำได้ เช่น \(r=\{(1,2),(2,5),(0,4)\}\) นำไปใส่กราฟได้ว่า (ฝั่งซ้าย)

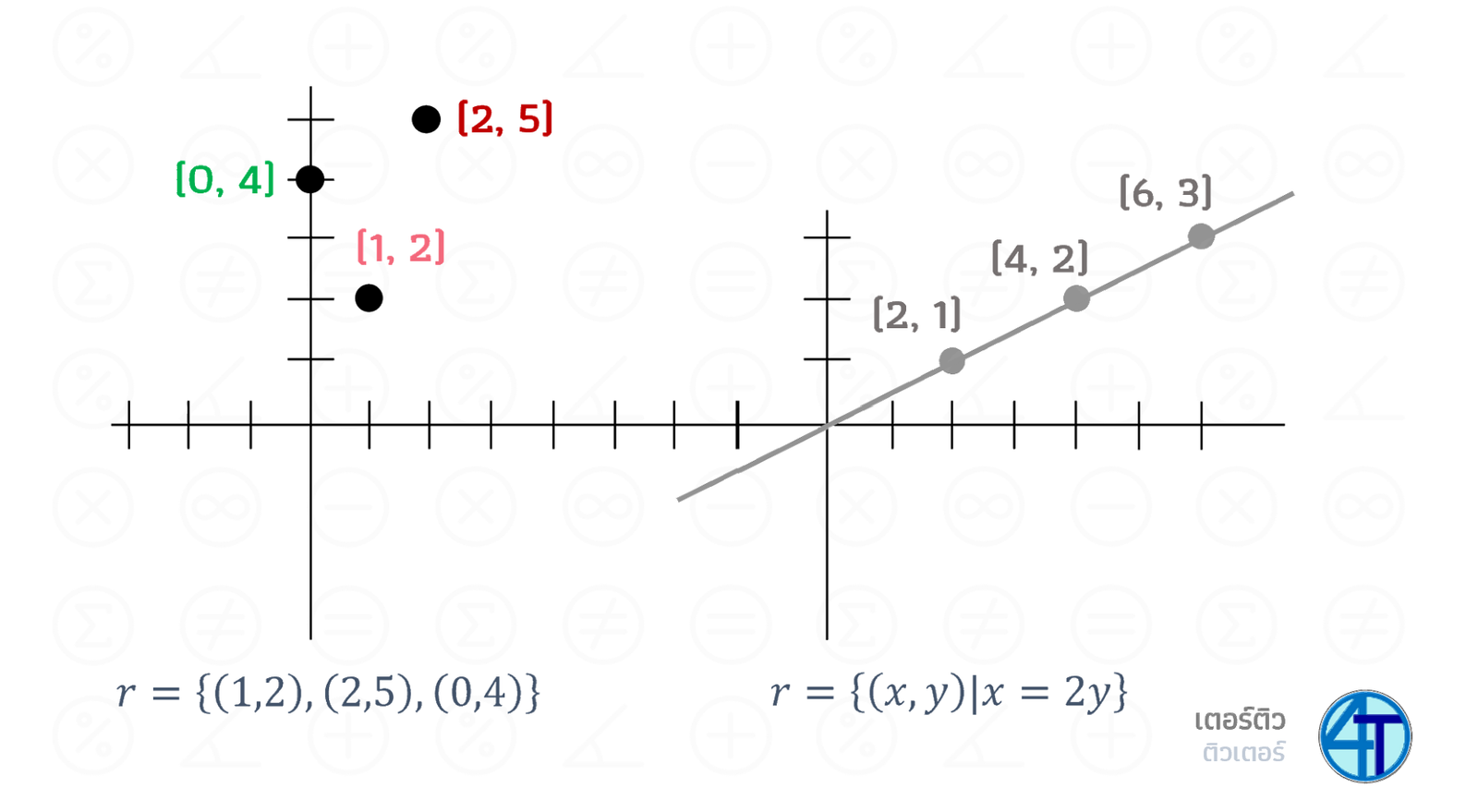
แต่หากเรามีความสัมพันธ์ที่เป็นสมการ เช่น \(r=\{(x,y)\;|\;x=2y\}\) (การที่ไม่เขียนบอกเซตในความสัมพันธ์เช่น \(A\times A\) หรือ \(A\times B\) จะเป็นที่รู้กันเลยว่า เราจะใช้เซต จำนวนจริง นั่นก็คือ \(x\) กับ \(y\) เป็นจำนวนจริงอะไรก็ได้ ที่ตรงกับเงื่อนไขความสัมพันธ์) โจทย์บอกว่า \(x=2y\) ดังนั้น สมมติเช่นเรามี \(x=2\) เราก็จะได้ว่า \(y=1\) ตัวอื่น ๆ เช่น \((x,y)=(4,2),(6,3)\) เป็นต้น สังเกตว่ามันมีเยอะมากเลย ดังนั้น การวาดกราฟ เราจะพล็อตจุดตัวอย่างมาคร่าว ๆ ให้เห็นรูปแบบ และจะลาดเส้นเชื่อมจุดเอง อย่างในรูปด้านขวาภาพบน

กราฟความสัมพันธ์ของอสมการ

อีกรูปแบบคือกราฟความสัมพันธ์ที่เป็นพื้นที่ เช่น \(r=\{(x,y)\;|\;x\lt 2y\}\) แบบนี้คือสมมติเราเลือก \(x\) มา เราจะสามารถเลือก \(y\) ตัวไหนก็ได้ที่ \(2y\) มันมีค่า "มากกว่า" \(x\) ซึ่งข้อนี้เราพูดถึงจำนวนจริงทั้งหมด \(\mathbb{R}\) เพราะโจทย์ไม่ได้กำหนดเซตมาให้

วิธีการวาดกราฟความสัมพันธ์ เรามักจะ เปลี่ยนเครื่องหมายเป็นเครื่องหมาย เท่ากับ ก่อน (ถ้าสมการเป็นรูปแบบแปลก ๆ ให้จัดรูปเป็น \(y\) ในรูปของ \(x\) หรือ \(x\) ในรูปของ \(y\) ก่อนนะ) แล้วจึงหาว่าจะแรเงาที่ส่วนไหนของกราฟ ข้อนี้เราจะแปลงเป็น \(x=2y\) ได้ความสัมพันธ์ตามรูป ลองสมมติจุดมาคร่าว ๆ เช่น \((2,1),(4,2),(6,3)\) 

เมื่อเราได้แล้ว เราจะมาวิเคราะห์ว่าจะแรเงาตรงไหนดี เนื่องจากข้อนี้เราเขียน \(x\) ในรูปของ \(y\) (สังเกตได้จาก สมการข้างซ้าย เป็นตัว \(x\) ตัวเดียว \(=\) อะไรสักอย่าง \(y\)) ดังนั้น เราจะใช้ตัว \(y\) เป็นตัวตั้งต้น พูดง่าย ๆ คือ เราจะหยิบ \(y\) แล้วทำสมการด้านขวา จนได้ว่า \(x\) เท่ากับเท่าไหร่ แต่สมการจริง ๆ ที่เรามี มันไม่ใช่เครื่องหมาย \(=\) แปลว่า เราจะแรเงาตามฝั่ง เครื่องหมาย \(\lt\) หรือ \(\gt\)

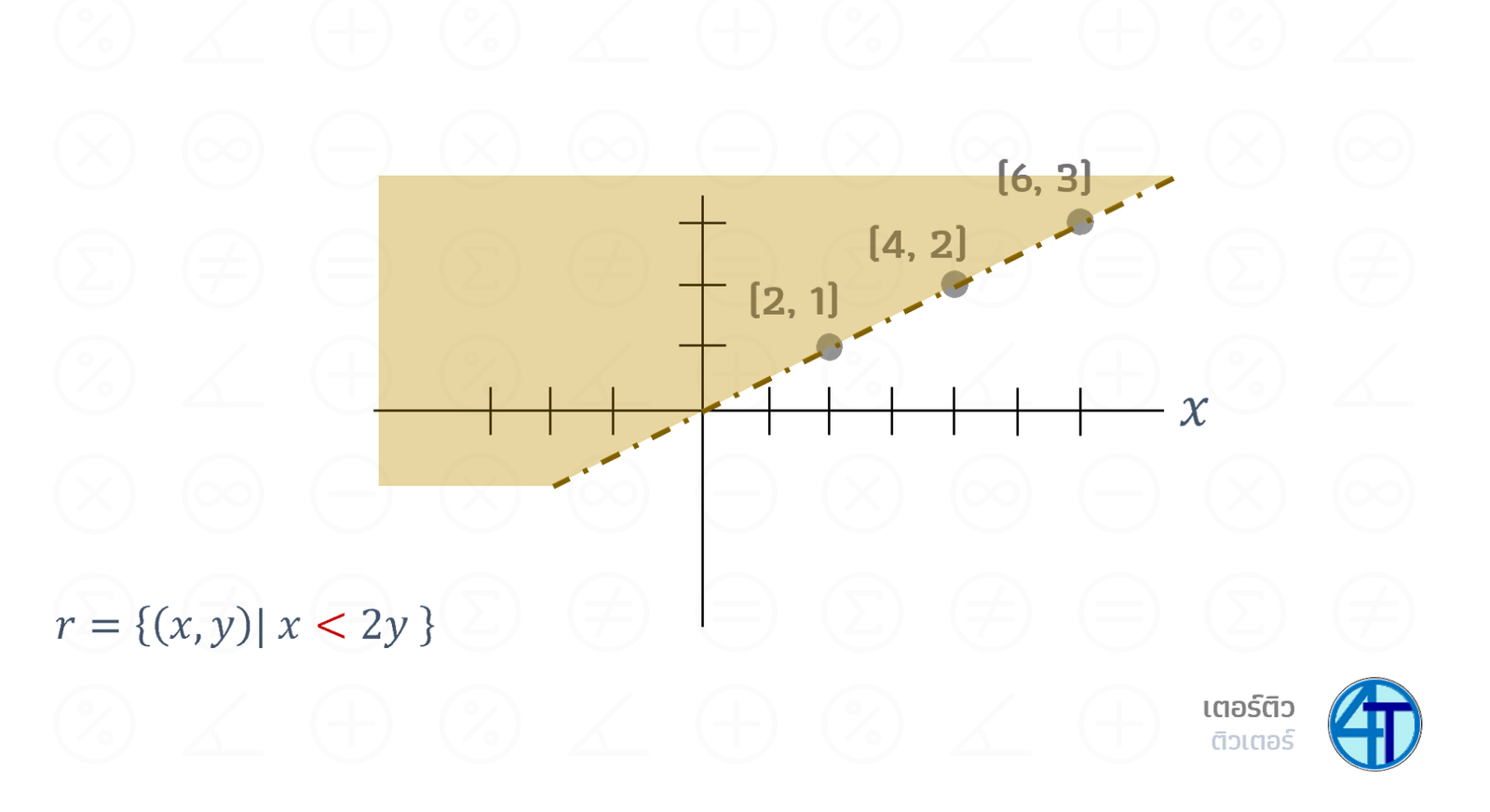
เมื่อเราเขียน \(x\) ในรูป \(y\) แบบนี้ เราจะแรเงาไป ทางซ้ายเพราะ \(x\) ต้องน้อยกว่า และการน้อยกว่า เราจะเปลี่ยนเส้นที่เราวาด \(x=2y\) เป็นเส้นประ แปลว่า ตรง \(x=2y\) เราไม่เอานะ

เรื่องการวาดกราฟไม่ยากมาก แต่ต้องมองให้เป็นหลักการ ดังนั้น หากใครสนใจเพิ่มเติมสามารถดูที่วิดีโอสอนในส่วนนี้ได้เลยนะครับน้อง ๆ การที่เราเห็นภาพและเสียงไปด้วย จะช่วยให้น้องเข้าใจเรื่องการวิเคราะห์กราฟความสัมพันธ์ได้ดีมากขึ้น

ตัวอย่าง 1 จงวาดกราฟของความสัมพันธ์ \(\{(x,y)\;|\;|y|\ge x\}\)

ให้เราทำขั้นตอนแรก คือ เปลี่ยนเป็นเครื่องหมาย \(=\) และจัดรูป เนื่องจากฝั่งซ้ายเป็น \(|y|\) การจัดรูปแบบสุด ๆ เลย คือ เหลือแค่ \(x\) หรือ \(y\) ฝั่งซ้าย แบบไม่ติดอะไร ดังนั้น พี่จะสลับฝั่งเป็นแบบนี้

เราจะได้ว่า เราเขียน \(x\) ในรูปของ \(y\) ดังนั้น หลักการก็คือ สุ่มแทนจุด โดยการเลือกค่า \(y\) ใด ๆ มาเพื่อคิดคำนวณหาค่า \(x\) ตัวอย่างจุดที่เราจะใช้คือ \((0, 0), (1, 1), (1, -1), (2, 2), (2, -2)\)

และเนื่องจากข้อนี้เครื่องหมายเป็น \(x\le |y|\) ดังนั้น เราจะแรเงาฝั่งซ้ายของเส้น (ค่า \(x\) ไปทางซ้าย แปลว่า "น้อยกว่า") และเส้นก็ยังเป็นเส้นทึบ เพราะเราเอา \(x=|y|\) ด้วยนั่นเอง