เลือกอ่านตามหัวข้อ?
เกริ่นโดเมนและเรนจ์

เรื่องนี้เป็นเรื่องที่ออกข้อสอบค่อนข้างบ่อย และเป็นโจทย์ที่หากคิดไม่ดี มักจะทำผิดหรือลืมบางตัวไปเสมอ ดังนั้น เราจะมาพูดเรื่องนี้ ในเชิงคอนเซปต์ และสรุปตบท้ายให้ว่า ข้อควรระวังที่น้องควรรู้ตอนทำโจทย์เรื่อง การหาโดเมนและเรนจ์ มันมีอะไรบ้าง ก่อนอื่นเรื่องนี้ เป็นเรื่องเดียวกันกับ โดเมนและเรนจ์ของฟังก์ชันนะครับ ดังนั้น พี่จะรวมพูดไปด้วยกันเลย ในบทของฟังก์ชันน้องจะเรียนรู้กันอีกทีว่า ฟังก์ชันกับความสัมพันธ์มันต่างกันยังไง แต่มันไม่ต่างมาก จริง ๆ มันแทบจะเป็นตัวเดียวกันด้วยซ้ำ
อย่างที่เรารู้กันแล้วว่า ความสัมพันธ์คือ คู่อันดับ ที่จับตัวหน้ากับตัวหลัง จากสองเซต อาจเป็นเซตเดียวกันก็ได้ เช่น เซตจำนวนจริงทั้งคู่ \(\mathbb{R}\times\mathbb{R}\)
(1) ตัวหน้า (2) ตัวหลัง นี่แหละครับน้อง ๆ คือคีย์เวิร์ดสำคัญเลย
เซตของตัวหน้าทั้งหมด คือ โดเมน
เซตของตัวหลังทั้งหมด คือ เรนจ์
ยกตัวอย่าง เช่น ความสัมพันธ์ \(\{(1,3), (1,4), (2,5), (0,9)\}\) จะเห็นว่า ตัวหน้าทั้งหมด คือ \(0, 1, 2\) เราจะเรียกทั้งหมดว่า โดเมน นั่นเอง โดย โดเมนเนี่ยมันเป็นเซตของตัวหน้าทั้งหมด ดังนั้น ความสัมพันธ์ข้างต้นเลยมีโดเมน คือ \(\{0,1,2\}\)
ในทางเดียวกัน ตัวหลังที่เป็นไปได้ทั้งหมด คือ เรนจ์ ซึ่งมี \(3,4,5,9\) ดังนั้น เรนจ์ของความสัมพันธ์คือ เซตของตัวเลขพวกนั้น หรือ \(\{3,4,5,9\}\)
โดเมน ของความสัมพันธ์ \(r\) คือ \(D_r\)
เรนจ์ ของความสัมพันธ์ \(r\) คือ \(R_r\)
เมื่อเรารู้สัญลักษณ์ จับรวมกันทั้งหมดข้างบนจะได้ว่า
\(r=\{(1,3), (1,4), (2,5), (0,9)\}\)
มี \(D_r=\{0,1,2\}\)
มี \(R_r=\{3,4,5,9\}\)
แบบข้างบนที่เจอเป็นแบบที่ โจทย์แจกแจงคู่อันดับทุกตัวมาให้น้อง ๆ แล้ว สิ่งที่น้องทำก็แค่ดูว่า ตัวอะไรเป็นตัวหน้าบ้าง นำไปใส่ในเซตของโดเมน ตัวไหนอยู่ตัวหลังบ้าง นำไปใส่ในเซตของเรนจ์ ซึ่งมันไม่ได้ซับซ้อนอะไร ในเรื่องต่อไป เราจะไปดูแบบที่โจทย์บอกความสัมพันธ์เป็นสมการมา แล้วน้องจะต้อง โดเมนกับเรนจ์
แบบที่ 1 แจกแจงสมาชิกได้อยู่
ตัวอย่างโจทย์ คือ สมมติ เรามี \(A=\{-2, -1, 0, 1, 2\}\) และ \(r=\{(x,y)\in A\times A\;|\;y=x^2\}\) เราต้องวิเคราะห์โจทย์ได้แล้วว่า โจทย์ให้หยิบตัวเลขจาก \(A\) มาเป็นได้ทั้งตัวหน้าตัวหลัง เพราะ เป็นความสัมพันธ์บนเซต \(A\) หรือ \(A\times A\) นั่นเอง โดยที่เมื่อหยิบมา \((x,y)\) แบบนี้ ความสัมพันธ์คือ \(y=x^2\)
การทำโจทย์ประเภทนี้ ให้น้องสังเกตว่า สมการฝั่งซ้ายคือ \(y\) ซึ่งเป็นตัวแปรเดียวโดด ๆ แต่ฝั่งขวาเป็น \(x^2\) ดังนั้น สมมติ เราเลือกหยิบตัวหลังก่อน หรือ \(y\) เราต้องไปหาอีกว่า \(y=x^2\) แปลว่า ตัวอะไรนะที่กำลังสองได้ \(y\) แต่หาก เราเลือกหยิบ \(x\) มาก่อน (ตัวหน้า) เราจะสามารถแทนค่าเข้าไปได้เลย เพื่อได้ \(y\) กลับมา
ดังนั้น หยิบ \(x\) มา แล้วไปแทนหา \(y\) จะง่ายกว่า
เมื่อ \(x=-2\) จะได้ว่า \(y=x^2=(-2)^2=4\) แต่ไม่มีทางเป็นไปได้ เพราะ มันไม่อยู่ในเซต \(A\) หมายความว่า \(y\) ซึ่งคือตัวหลัง เราต้องเลือกหยิบจากเซต \(A\) เช่นกัน แต่ไม่มี \(4\) ดังนั้น คู่อันดับ \((-2,4)\) ถึงจะถูกต้องตามความสัมพันธ์ \(y=x^2\) แต่เราใช้ไม่ได้ เพราะไม่ใช่ คู่อันดับที่มาจาก \(A\times A\)
เมื่อน้องลองหยิบ \(x\) จากเซต \(A\) ทั้งหมด จะเห็นว่ามีคู่อันดับที่เป็นไปได้ ดังนี้
\(r=\{(-1, 1), (0, 0), (1, 1)\}\)
แปลว่า \(D_r=\{-1,0,1\}\) และ \(R_r=\{0, 1\}\)
โจทย์ประเภทนี้ไม่ค่อยออกข้อสอบครับ เพราะว่ามันง่ายโดยการที่น้อง ค่อย ๆ ลองหยิบ ๆ มาแทนค่าแล้วก็ตอบ โจทย์ส่วนมากที่จะเจอ คือ ความสัมพันธ์บนเซตจำนวนจริง แปลว่า เราไม่สามารถเลือกแทนทุกค่าได้ ซึ่งเราจะไปดูกันต่อที่พาร์ทต่อไปกัน
แบบที่ 2 วิเคราะห์หาตัวที่เป็นไปไม่ได้ (แจกแจงไม่ได้)
ตัวอย่างโจทย์ \(r=\left\{(x,y)\;|\;y=\sqrt{x-5}\right\}\) หลักการทำโจทย์ประเภทนี้ เนื่องจาก \(x,y\) สามารถเป็นเลขอะไรก็ได้ในจำนวนจริง บางคนอาจจะบอกว่า แสดงว่า \(D_r=R_r=\mathbb{R}\) หรือเปล่า? คำตอบ คือ ไม่เสมอไปครับ
ลองดูกรณี \(x=0\) ก็ได้ เมื่อน้องแทนในสมการ \(y=\sqrt{x-5}=\sqrt{0-5}=\sqrt{-5}\) ใต้รูทเป็นจำนวนติดลบ ซึ่งไม่มีจริงในจำนวนจริง แปลว่า \(x\) เป็น \(0\) ไม่ได้นะ อะไรประมาณนี้
แล้วจะหาโดเมนกับเรนจ์ยังไงให้เป็นหลักการดี
ต้องกลับไปที่ไอเดีย การแทน \(x\) เพื่อหา \(y\) ครับ จำกันได้ไหมเอ่ย ที่เคยพูดกันไปในตอนที่แล้วว่า หากสมการของเรามี ฝั่งซ้าย เป็นตัวแปรเดียวโดด ๆ ในกรณีนี้ คือ \(y\) และฝั่งขวา วุ่นวาย กรณีนี้คือ \(\sqrt{x-5}\) เราจะเลือก แทนค่าฝั่งขวา หรือการเลือกแทนค่า \(x\) นั่นเอง เพื่อหา \(y\) เช่น \(x=6\) จะได้ว่า \(y=\sqrt{x-5}=\sqrt{6-5}=1\)
ดังนั้น โจทย์เราเลยกลายเป็นว่า เราแทน \(x\) ตัวไหนได้บ้าง ใน \(\sqrt{x-5}\) เป็นที่มาของการหาโดเมนนั่นเอง ค่า \(x\) ตัวไหนที่แทนใน \(\sqrt{x-5}\) ไม่ได้ ก็แปลว่า ใช้ไม่ได้ ดังนั้นก็ไม่อยู่ใน \(D_r\) ของเรา
การหาโดเมน
เพราะฉะนั้น หลักการการหาโดเมน คือ จัดรูปสมการให้อยู่ในรูป \(y=\) ก้อนบ้า ๆ ของ \(x\) จากนั้นเราจะมี 2 ตัวหลัก ๆ คือ
1. ใต้รูทห้ามติดลบ
2. ตัวส่วนห้ามเป็น \(0\)
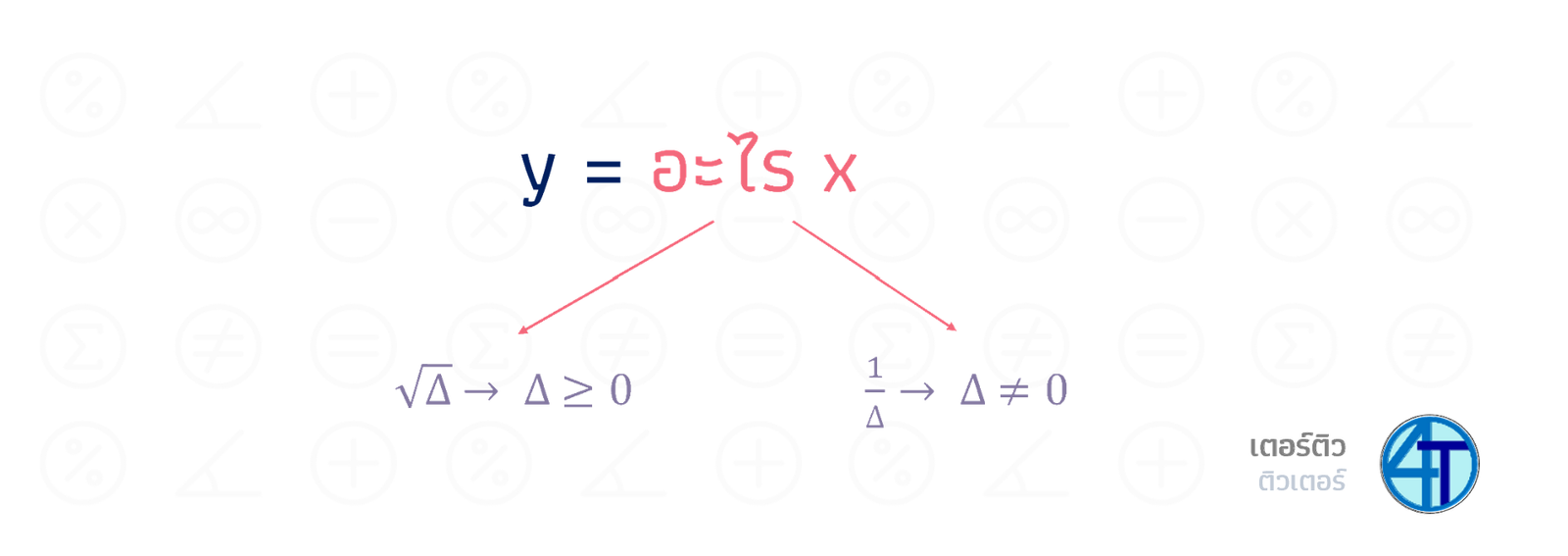
สมมติ โจทย์ให้หาโดเมนของ \(y=\sqrt{x-5}\) เนื่องจากสมการจัดรูปมาในรูปที่เราต้องการหาโดเมนแล้ว เราจะได้ว่า มีรูทอยู่ แต่ไม่มีเศษส่วน ดังนั้น ก็จะมีข้อจำกัดข้อเดียว คือ ใต้รูทไม่ติดลบ
\(\require{cancel} \begin{aligned} x-5&\ge0\\ x&\ge5 \end{aligned}\)
เราจะได้เลยว่า โดเมนของข้อนี้คือ \(D_r=[5, \infty)\) เราจะเขียนเป็นช่วงคำตอบเหมือนที่เราเรียนกันในเรื่อง อสมการ
อีกตัวอย่าง จงหาโดเมนของ \(y=\dfrac{x+3}{x-2}\) เนื่องจากต้องการหาโดเมน ดังนั้น ต้องจัดรูป \(y=\) อะไรของ \(x\) ซึ่งเป็นตามที่ต้องการอยู่แล้ว ข้อนี้ ไม่มีรูท แต่มีเศษส่วน ดังนั้น ส่วนไม่เป็น \(0\)
\(\require{cancel} \begin{aligned} x-2&\ne0\\ x&\ne2 \end{aligned}\)
\(D_r=\mathbb{R}-\{2\}\) หรือพูดง่าย ๆ คือ เป็นอะไรก็ได้ ยกเว้น \(2\)
การหาเรนจ์
เนื่องจาก เรนจ์ คือค่า \(y\) ดังนั้น ไอเดียเหมือนกันครับน้อง ๆ ถ้าเราสามารถจัดรูป \(x=\) ก้อนบ้า ๆ ของ \(y\) เราก็เลือกแทนค่า \(y\) ได้ โดยมีข้อจำกัดสองข้อเหมือนเดิมคือ (1) ใต้รูทไม่ติดลบ (2) ส่วนไม่เป็นศูนย์ ดังนั้น ในหัวข้อนี้ พี่จะพูดถึงการจัดรูปสมการเป็นส่วนมาก เพราะ ปกติแล้ว โจทย์จะให้
\(y=\) อะไรของ \(x\)
แต่เราอยากได้
\(x=\) อะไรของ \(y\)
ซึ่งต้องใช้การจัดรูปสมการนั่นเอง

ดังนั้น สิ่งสำคัญที่สุดในเรื่องนี้ คือ การจัดรูปสมการ ตัวอย่างง่ายสุด เช่นเรามีสมการ \(y=x+5\) เราอยากจัดรูปสมการนี้ให้เป็นรูป \(x=\) อะไร \(y\) ดังนั้น เราก็แค่ พยายามย้ายทุกอย่างให้เหลือแต่ \(x\) อยู่ฝั่งเดียว จะได้ว่า \(x=y-5\) นั่นเอง
ถ้ายากขึ้นมาหน่อย ก็พวก
(1) ยกกำลัง
(2) การถอดรูท
สมมติเรามี \(y=x^2+5\) เมื่อเราย้ายไปตัว \(x\) จะยังติดกำลังสอง ดังนี้
\(\require{cancel} \begin{aligned} y&=x^2+5\\ y-5&=x^2 \end{aligned}\)
แต่เราอยากได้ \(x\) เดี่ยว ๆ ถูกไหมครับ ดังนั้น น้อง ๆ ต้องจัดการเลขยกกำลังสองที่มันติดอยู่กับ \(x\) โดยการ ถอดรูทมันซะ อย่าลืมว่าต้องใส่เครื่องหมาย \(\pm\) เสมอนะ
\(\require{cancel} \begin{aligned} y-5&=x^2\\ \textcolor{blue}{\pm}\sqrt{y-5}&=x \end{aligned}\)
เมื่อได้แล้ว เราจะรู้ทันทีว่า เรนจ์ของสมการคือ ใต้รูทต้องไม่ติดลบ นั่นคือ
\(\require{cancel} \begin{aligned} y-5&\ge0\\ y&\ge5 \end{aligned}\)
เพราะฉะนั้น \(R_r=[5, \infty)\)
การจัดรูปที่พี่อยากเน้นมีสองข้อควรระวังครับ
(1) ถอดรูทต้องใส่ \(\pm\) ด้วย
(2) หากยกกำลังสองเพื่อกำจัดรูท ต้องโน้ตไว้เสมอว่าคำตอบของรูท ไม่มีทางติดลบ
บางโจทย์ เราอาจจะช็อคได้เพราะมันจัดรูปย้ายข้างแบบโง่ ๆ ไม่ได้ เช่น สมมติเรามี \(y=x^2+4x-10\) หากเราต้องการหาเรนจ์ เราต้องจัดรูป \(x=\) อะเไรของ \(y\) แต่เมื่อเราลองย้ายยังไงมันก็ยังไม่เหลือ \(x\) ตัวเดียวอยู่ดี

ดังนั้น วิธีการที่จะมาช่วยเราได้ เช่น การจัดรูปกำลังสองสมบูรณ์ ครับ หลักการนี้เป็นหลักการที่ใช้บ่อยมาก ดังนั้น พี่จะแยกไปพูดใน หัวข้อถัดไปเป็นหัวข้อใหญ่เลย
จัดรูปสมการกำลังสองสมบูรณ์
อย่างที่บอกในการหาโดเมนกับเรนจ์ บางทีเราต้องจัดรูปสมการให้อยู่ในรูปที่ต้องการ ทวนอีกที
หาโดเมน ให้จัดรูป \(y=\) อะไรของ \(x\)
หาเรนจ์ ให้จัดรูป \(x=\) อะไรของ \(y\)
ในส่วนนี้เราจะมาลงลึกกันในเรื่องของการ จัดรูปสมการกำลังสองสมบูรณ์ ในการหาโดเมนกับเรนจ์ ตัวอย่างโจทย์ เข่น \(y=x^2+4x-10\) เนื่องจาก เราเห็นกันแล้วว่า เราไม่สามารถจัดรูปแบบปกติได้ตามภาพด้านบน
สมการพหุนามกำลังสองแบบนี้ เราสามารถใช้หลักการจัดรูปสมการกำลังสองสมบูรณ์ได้ครับ ซึ่งปกติแล้วกำลังสองสมบูรณ์ เรามีสมการว่า

ปกติแบบง่ายคือเราจะมีสปส. หน้าพจน์ \(x^2\) เป็น \(1\) ดังนั้น สิ่งที่เราได้ก็จะเป็นเหมือนสมการล่างในรูปครับ คือ เราต้องหา หลัง (ล) จากพจน์กลาง
สมการเราคือ \(y=x^2+4x-10\) ซึ่งพจน์กลางคือ \(4x\) ตรงกับ \(2x\) คูณ หลัง แปลว่า หลัง (ล) ของเราก็คือ \(2\) นั่นเอง เมื่อเราได้ \(2\) มาแล้ว เราจะนำไปสร้างกำลังสองสมบูรณ์ดังนี้
\(x^2+2x\textcolor{blue}{(2)}+\textcolor{blue}{(2)}^2\) จะได้ \(x^2+4x+4\) แต่สิ่งที่เราต้องการ คือ \(x^2+4x-10\) ดังนั้น เราเลยต้องนำไปลบ \(14\) เพิ่มอีก เพื่อให้ได้ตามโจทย์ ดังนั้น หลักการที่อยากให้น้อง ๆ ดูคือ เราสร้างกำลังสองสมบูรณ์โดยใช้พจน์กลางมาช่วย จากนั้นเราจะได้พจน์หลังมา ซึ่งมันจะไม่ตรงกับโจทย์ เราต้องหาตัวเลขมาเพิ่ม
\(\require{cancel} \begin{aligned} x^2+4x-10\\ &=x^2+4x+4-14\\ &=(x+2)^2-14 \end{aligned}\)
เราจึงนำสิ่งที่รู้กลับไปแทนในโจทย์
\(\require{cancel} \begin{aligned} y&=x^2+4x-10\\ y&=x^2+4x+4-14\\ y&=(x+2)^2-14\\ y+14&=(x+2)^2\\ \pm\sqrt{y+14}&=x+2\\ \pm\sqrt{y+14}-2&=x \end{aligned}\)
เมื่อเราได้แล้ว เราจะเห็นว่ามีข้อจำกัดคือ ใต้รูทห้ามติดลบ ดังนั้น \(y+14\ge0\) แปลว่า \(y\ge-14\)
\(R_r=[-14,\infty)\)
ซึ่งจริง ๆ แล้วโจทย์พวกนี้ ออกบ่อยมาก และ น้องไม่จำเป็นต้องจัดรูปจนสุดก็ได้ ในส่วนสุดท้ายเราจะไปดูวิธีการ สังเกตรูปแบบสมการ เพื่อหาโดเมนและเรนจ์กันครับ
สังเกตรูปสมการ
ขออนุญาตยกตัวอย่าง คล้าย ๆ รูปกำลังสองที่เราเรียนรู้กันไปแล้วด้านบน สมมติเรามีโจทย์ว่า \(y=x^2+6x-1\) หากเราอยากหาเรนจ์ ช่วงของ \(y\) ที่เป็นไปได้ เราจะทำการจัดรูป \(x=\) อะไรของ \(y\) ซึ่งบางทีก็เสียเวลาครับ
\(\require{cancel} \begin{aligned} y&=x^2+6x-1\\ y&=(x+3)^2-10 \end{aligned}\)
หากเราจัดรูปมาถึงแค่นี้ เราก็รู้เลยว่า เรนจ์คือ \([-10,\infty)\) นะ ถามว่าทำไมถึงรู้ ? น้องลองสังเกตสมการดี ๆ ครับ ตรงพจน์กำลังสองสมบูรณ์
เรารู้กันอยู่แล้วว่า ไม่ว่าอะไรกำลังสองก็จะเป็นบวกเสมอ ดังนั้นแปลว่า พจน์
\(\require{cancel} \begin{aligned} (x+3)^2&\ge0 \end{aligned}\)
พอเรานำไป \(-10\) ทั้งสองข้างสมการ เราก็จะได้ตามสมการเริ่มต้น ซึ่งคือตัว \(y\) นั่นเองครับ
\(\require{cancel} \begin{aligned} (x+3)^2-10&\ge-10\\ y&\ge-10 \end{aligned}\)
\(R_r=[-10,\infty)\)
ดังนั้น พี่อยากให้น้องลองกลับไปอ่านในพาร์ทที่แล้วเรื่องการจัดรูปกำลังสองทุกข้อเลยครับ น้องจะเห็นว่า มันหยุดคิดประมาณสองสามบรรทัดแรกได้เลย ไม่ต้องคิดจนสุด
เราเรียกวิธีแบบนี้ว่า การจัดรูปให้ได้สมการที่เรามี โดยใช้ความรู้ที่เรารู้กันมาอยู่แล้ว เช่น
(1) กำลังสอง \(\ge0\) เสมอ
(2) ค่าสัมบูรณ์ \(\ge0\) เสมอ
อีกตัวอย่าง สมมติเรามี \(y=3-(1-x)^2\) เราจะหาเรนจ์กันครับ โดยเรารู้ว่า
\(\require{cancel} \begin{aligned} (1-x)^2&\ge0\\ -(1-x)^2&\le0\\ 3-(1-x)^2&\le3\\ y&\le3\\ \end{aligned}\)
เราเลยได้ว่า \(R_r=(-\infty, 3]\)
ข้อควรระวัง อยากให้สังเกตว่า พี่คูณลบเข้าไปเพื่อกลับเครื่องหมาย จากบรรทัด (1) ไป บรรทัด (2) ก่อน เพราะเราไม่สามารถนำ \(3\) ไปลบเลยแบบนี้ได้
\(\require{cancel} \begin{aligned} (1-x)^2&\ge0\\ 3-(1-x)^2&\ge3-0\;\;\text{(wrong)}\\ \end{aligned}\)
แบบนี้คือผิดนะ อย่าสับสน หากสงสัยว่าทำไมไม่ได้ ก็ลองนึกภาพตามก็ได้ครับ ตอนแรกฝั่งซ้าย มากกว่า ฝั่งขวา พอเรานำอะไรมาลบ แปลว่า ฝั่งซ้าย เราลบออกมากกว่า ค่ามันจึงน้อยกว่า ฝั่งขวานั่นเอง
ค่าสัมบูรณ์
ค่าสัมบูรณ์ก็เป็นอีกหนึ่งตัวครับ ที่น้อง ๆ จะเจอหลักการก็เหมือนเดิม ค่าสัมบูรณ์เป็นบวกเสมอ ดังนั้น เราจะพยายามจัดรูปให้มันได้ตามสมการตั้งต้นเหมือนกัน สมมติว่าเรามี \(y=|x+5|-7\) เรารู้ว่า
\(\require{cancel} \begin{aligned} |x+5|&\ge0\\ |x+5|-7&\ge-7\\ y&\ge-7 \end{aligned}\)
ดังนั้น \(R_r=[-7,\infty)\) นั่นเอง
อีกแบบที่ยากขึ้นไปอีก คือมีมาหลาย ๆ ตัว เช่น \(|y|+|x+6|=5\)
ข้อนี้ เราจะย้ายข้างไปสักเล็กน้อย สมมติเราต้องการหาโดเมน เราต้องจัดรูป \(y=\) อะไรของ \(x\)
\(\require{cancel} \begin{aligned} |y|=5-|x+6| \end{aligned}\)
สังเกตว่า มันเกือบจะเป็นสิ่งที่เราได้แล้ว อย่าไปกลัวครับน้อง ลองคิดก่อนก็ได้ติดมันทั้ง ๆ แบบนี้แหละ หลักการเดิม
\(\require{cancel} \begin{aligned} |x+6|&\ge0\\ -|x+6|&\le0\\ 5-|x+6|&\le5\\ |y|&\le5 \end{aligned}\)
ตอนนี้เราติด \(|y|\le5\) สบายเลยครับ กลับไปที่เรื่อง อสมการค่าสัมบูรณ์ เราจะได้ \(-5\le y\le 5\) ซึ่งก็คือเรนจ์นั่นเอง \(R_r=[-5,5]\)
หากต้องการหาโดเมน ก็เหมือนเดิมครับ พยายามจัดรูป \(y=\) อะไรของ \(x\)
\(\require{cancel} \begin{aligned} |x+6|=5-|y| \end{aligned}\)
ฝั่งซ้ายยังติดค่าสัมบูรณ์ทำให้เราทำอะไรกับ \(+6\) ไม่ได้เลย ไม่เป็นไรครับลองดูทั้ง ๆ แบบนี้แหละ
\(\require{cancel} \begin{aligned} |y|&\ge0\\ -|y|&\le0\\ 5-|y|&\le5\\ |x+6|&\le5 \end{aligned}\)
จาก \(|x+6|\le5\) เราก็ใช้เรื่องอสมการค่าสัมบูรณ์มาช่วย
\(\require{cancel} \begin{aligned} -5&\le x+6\le5\\ -11&\le x\;\;\;\;\;\;\le -1 \end{aligned}\)
โดเมนเราคือ \(D_r=[-11,1]\)
ส่วนโจทย์ PAT อะไรพวกนี้ก็ออกไม่ต่างจากนี้มากครับ แต่จะนำทุกอย่างในหน้านี้มารวมกันทั้งหมด ทำให้เราสับสนได้ ว่าจะคิดอะไรก่อนดี ดังนั้น ในส่วนของโจทย์เพิ่มเติมที่ยากขึ้นและวิธีการคิด พี่จะขอเก็บไปพูดในวิดีโอที่สอนในหน้านี้ทีเดียว หากใครสนใจก็สามารถรับชมได้ที่ด้านบนหน้าเว็บนี้ได้เลยครับ
หากบทความพี่เป็นประโยชน์ ฝากแชร์ต่อให้เพื่อนๆ ด้วยนะครับ :')

