อสมการค่าสัมบูรณ์ ม.4

เลือกอ่านตามหัวข้อ?

- สรุปรูปแบบที่เจอบ่อย ๆ

- การแก้อสมการค่าสัมบูรณ์

\(|x|\lt a\)

\(|x|\gt a\)

\(|x|\) กระทำกับ \(|y|\) (ค่าสัมบูรณ์ทั้งสองฝั่ง)

อยากดูแบบวิดีโอ? (อยู่ระหว่างการจัดทำคลิป)

การแก้อสมการค่าสัมบูรณ์

ก่อนจะเข้าบทนี้อย่าลืมไปอ่านเรื่อง สมการค่าสัมบูรณ์ กันก่อนนะครับ เนื่องจากมันคือเรื่องเดียวกัน และหลักการแก้ก็คล้าย ๆ กัน จะได้เห็นไอเดียการแก้ค่าสัมบูรณ์กันก่อน ว่าถ้าติดค่าสัมบูรณ์จะต้องกำจัดมันออกยังไง เราไปดูรูปแบบที่พบบ่อยกันดีกว่า

รูปแบบที่ 1

\(\require{cancel}\begin{aligned} |x|&\lt a\\ |x|&\le a\\ \end{aligned}\)

แบบนี้ให้เราสังเกตง่าย ๆ เลยก็ได้สมมติ \(|x|\lt 5\) มันแปลว่า ค่าของ \(x\) มีค่าน้อยกว่า 5 แบบไม่คิดเครื่องหมาย ดังนั้น มันจะเป็นช่วงตั้งแต่ \(-5\) ถึง \(5\) และการเอา \(5\) หรือไม่เอา \(5\) ก็ขึ้นอยู่กับเครื่องหมายของอสมการนั่นเองครับ ดังนั้น การที่เราบอก \(|x|\lt a\) หรือ \(|x|\le a\) มันจะเป็นสองกรณี ดังนี้

ดังนั้น หากเจอโจทย์ประเภทนี้ ก็ถอดค่าสัมบูรณ์เป็นสองสมการได้เลย อย่าลืมตรวจคำตอบ เพราะ \(a\ge 0\) เสมอ เนื่องจาก ฝั่งซ้ายเป็นค่าสัมบูรณ์ ดังนั้น เป็นบวกเสมอ และ \(a\) มากกว่าฝั่งซ้าย ดังนั้น \(a\) ก็เป็นบวกเสมอเช่นกัน

ตัวอย่าง จงหาเซตคำตอบของอสมการ \(|x+2|\lt 6\) เราก็แยกเป็นสองสมการเลยจะได้ว่า

\(\require{cancel}\begin{aligned} -6\lt x+2\lt 6 \end{aligned}\)

การเขียนสมการแบบนี้ จริง ๆ แล้ว เราสามารถแก้สมการโดยไม่ต้องแยกร่างได้ แต่ใครไม่ชิน ก็แยกเป็นสองกรณีแบบนี้ \(-6\lt x+2\) และ \(x+2\lt 6\) แต่พี่จะทำแบบไม่แยกไปเลย ได้ว่า

\(\require{cancel}\begin{aligned} -6-2&\lt x+2-2\lt 6-2\\ -8&\lt\;\;\;\;\;\;x\;\;\;\;\;\;\,\lt 4 \end{aligned}\)

ดังนั้นตอบ เซตคำตอบคือ \((-8, 4)\) นั่นเองครับ

ถ้าถามว่าจะแบ่งกรณีใช้ค่าวิกฤตได้ไหม

คำตอบก็คือได้เหมือนกันครับอย่างในข้อนี้ เราจะแบ่งเป็น 2 กรณี

กรณที่ 1 : \(x\ge-2\) แปลว่า \(x+2\) เป็นคนดี ก็เลยได้ว่าถอดค่าสัมบูรณ์ออกได้เลย

\(\require{cancel} \begin{aligned} x+2&\lt6\\ x&\lt 4 \end{aligned}\)

ดังนั้นแปลว่า คำตอบในกรณีนี้คือ \([-2, 4)\) เพราะต้องมากกว่า \(-2\) (เอา \(-2\) ด้วย) และน้อยกว่า \(4\)

กรณีที่ 2 : \(x\lt-2\) แปลว่า \(x+2\) เป็นคนไม่ดี ก็เลยถอดและต้องติดลบ

\(\require{cancel} \begin{aligned} -x-2&\lt6\\ -8&\lt x \end{aligned}\)

ดังนั้นแปลว่า คำตอบในกรณีนี้คือ \((-8, -2)\)

พอนำมารวมกัน คำตอบก็จะได้เหมือนกันว่า \((-8, -2)\cup[-2,4)=(-8,4)\) ดังนั้นจะเห็นได้เลยว่า วิธีแรกง่ายกว่าเพราะเราไม่ต้องเสียเวลาแบ่งกรณี เพราะฉะนั้นหากเจอโจทย์แบบนี้ ให้น้องทำแบบวิธีบนจะง่ายกว่า ลองไปฝึกทำตัวอย่างโจทย์ตามด้านล่างกันได้เลย

หาเซตคำตอบของ \(|x+2|\lt x+5\)

เฉลย

เราจะได้ว่า \(-(x+5)\lt x+2\lt x+5\) จะเห็นว่าเราไม่สามารถทำพร้อมกันทั้งสมการได้ ดังนั้นเราต้องคิดแยก

\(\require{cancel} \begin{aligned} -(x+5)&\lt x+2\\ -x-5&\lt x+2\\ -7&\lt 2x\\ -\dfrac{7}{2}&\lt x\\ \end{aligned}\)

และ

\(\require{cancel} \begin{aligned} x+2&\lt x+5\\ 2&\lt 5 \end{aligned}\)

เป็นจริงเสมอ สำหรับทุก \(x\)

อย่าลืมว่าการแบ่งกรณีแบบนี้ ต้องเชื่อมด้วย "และ" อย่าสับสนกับการแบ่งช่วงค่าวิกฤตที่น้องต้องนำมา "หรือ" กันเด็ดขาด ใครที่สับสน สามารถดูวิดีโอสอนเพิ่มเติมได้นะครับ ดังนั้น ข้อนี้หมายความว่า เราต้องทำสองคำตอบมา "และ" กัน

ตอบ \(\left(-\dfrac{7}{2},\infty\right)\cap\mathbb{R}=\left(-\dfrac{7}{2},\infty\right)\)

อย่าลืมเช็คคำตอบ ว่า \(|x+2|\ge 0\) แปลว่า ฝั่งขวา \(x+5\ge 0\to x\ge -5\) ซึ่งคำตอบที่เราได้ข้างบน ก็อยู่ (เป็นสับเซต) ในช่วงนี้ เราจึงได้ว่า คำตอบก็เป็นเหมือนเดิม

หาเซตคำตอบของ \(x+5\ge2|x|\)

เฉลย

ข้อนี้ดูไม่เหมือนสูตรมาก แต่ถ้าเราย้าย 2 ไปหารจะได้ว่า

\(\require{cancel} \begin{aligned} \dfrac{x+5}{2}\ge|x| \end{aligned}\)

เราก็จะได้สมการตามสูตร แค่ตัวค่าสัมบูรณ์มันอยู่ฝั่งขวาแค่นั้น เราเลยได้ว่า \(-\dfrac{x+5}{2}\le x\le \dfrac{x+5}{2}\) เราก็จะทำทีละข้าง และนำคำตอบมา "และ" กัน

\(\require{cancel} \begin{aligned} -\dfrac{x+5}{2}&\le x\\ -x-5&\le 2x\\ -3x&\le 5\\ x&\ge -\dfrac{5}{3} \end{aligned}\)

และ

\(\require{cancel} \begin{aligned} x&\le\dfrac{x+5}{2}\\ 2x&\le x+5\\ x&\le 5 \end{aligned}\)

นำมาและกันจะได้ว่า \(\left[-\dfrac{5}{3}, 5\right]\)

อย่าลืมตรวจคำตอบ ตัวที่ไม่ติดค่าสัมบูรณ์ต้องเป็นบวก เพราะ มัน \(\ge |x|\) เราเลยได้ว่าคำตอบสมการเป็นได้แค่ \(\dfrac{x+5}{2}\ge0\to x\ge -5\) ซึ่งคำตอบที่เราได้ไม่ได้ขัดแย้งหรือมีส่วนที่ต้องเอาออก ดังนั้น ก็ตอบเหมือนเดิม

รูปแบบที่ 2

\(\require{cancel} \begin{aligned} |x|&\gt a\\ |x|&\ge a \end{aligned}\)

แบบนี้เราต้องสังเกตก่อนว่า \(|x|\gt 4\) เราจะได้ว่าฝั่งบวก คือ มากกว่า 4 ก็ได้หมด แต่ฝั่งถ้า \(x\) ติดลบ คือต้องน้อยกว่า \(-4\) ลงไป เช่น \(-5, -10, -100,\dots\) ดังนั้น เราจะได้ ดังนี้

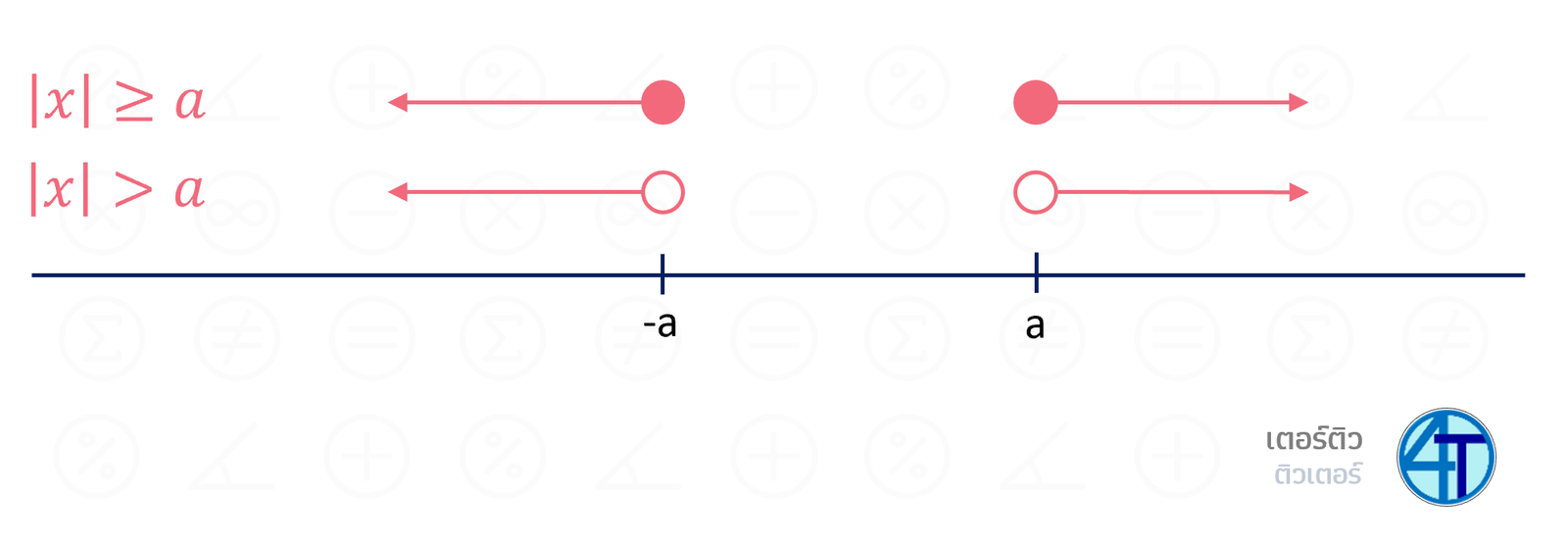
การแก้อสมการค่าสัมบูรณ์แบบนี้ การเชื่อมกันคือ "หรือ" นะ เพราะสองเส้นจำนวนมันไม่ทับกันถ้านำมา "และ" มันเป็นเซตว่าง ดังนั้น น้อง ๆ ต้องแยกให้ออกก่อนว่าตรงไหน "หรือ" ตรงไหน "และ"

เช่นหากต้องมีเซตคำตอบของ \(|x|\gt 3\) เราจะได้คำตอบคือ \(x\lt -3\) หรือ \(x\gt 3\) หรือเขียนง่าย ๆ ว่า \((-\infty,-3)\cup(3,\infty)\)

ข้อสังเกต กรณีแบบนี้ เราจะไม่ต้องตรวจคำตอบ เพราะฝั่งขวา (ไม่มีค่าสัมบูรณ์) จะเป็นอะไรก็ได้ (ลบหรือบวกก็ได้) ซึ่งต่างจาก รูปแบบ 1 ที่เราจะต้องตรวจคำตอบด้วยว่า ฝั่งขวาเป็นบวกเสมอ

หาเซตคำตอบของ \(|x+2|\gt x+3\)

เฉลย

อีกตัวอย่าง หาเซตคำตอบของ \(\left|\dfrac{x-1}{x+1}\right|\gt2\)

ข้อนี้จะใช้วิธีตามสูตรนี้ก็ได้ จะได้ว่า

\(\require{cancel} \begin{aligned} \dfrac{x-1}{x+1}\lt -2 \end{aligned}\)

หรือ

\(\require{cancel} \begin{aligned} \dfrac{x-1}{x+1}\gt 2 \end{aligned}\)

แต่จะสังเกตว่า เราก็จับคูณไขว้ไม่ได้อยู่ดี เพราะเป็นอสมการ เราไม่แน่ใจว่าตัวส่วนเป็นบวกหรือลบ วิธีที่ทำได้ คือ การแยกกรณีโดยกำหนด 2 แบบ (1) ส่วนเป็นบวก (2) ส่วนเป็นลบ จากนั้นคูณไขว้ได้ แต่สังเกตว่า เราจะมีต้องคิดทั้งหมด 4 (อันละ 2 กรณี 2 อัน) ซึ่งเยอะมาก เราจึงจะไปดูวิธีการแก้ข้อนี้ในรูปแบบที่สาม คือ การยกกำลังสองทั้งสองข้าง

รูปแบบที่ 3

\(\require{cancel} \begin{aligned} |x|&\lt|y|\\ |x|&\le|y|\\ |x|&\gt|y|\\ |x|&\ge|y| \end{aligned}\)

ก่อนอื่นต้องเกริ่นกันก่อนนิดนึงว่า การยกกำลังสองทั้งสองข้าง มันต้องกลับเครื่องหมายในบางกรณีด้วย ยกตัวอย่างง่าย ๆ สมมติเรามี

แบบนี้ไม่ต้องกลับเครื่องหมาย

\(\require{cancel} \begin{aligned} 5&\lt 7\\ 5^2&\lt7^2 \end{aligned}\)

แบบนี้ต้องกลับเครื่องหมาย

\(\require{cancel} \begin{aligned} -7&\lt -5\\ (-7)^2&\gt(-5)^2\\ 49&\gt 25 \end{aligned}\)

ดังนั้นมันแปลว่า การยกกำลังสองจริง ๆ แล้วมันทำตรง ๆ ไม่ได้ เพราะเราไม่รู้ว่าแต่ละฝั่งเป็นบวกหรือลบ แต่ข้อดีของ อสมการค่าสัมบูรณ์ ก็คือเราจะพอรู้ว่าแต่ละฝั่งเป็นบวกหรือลบ ดังนั้น เราสามารถดูได้ว่ายกกำลังสองได้หรือเปล่า เช่น \(|x+5|\) เป็นบวกเสมอ และ \(-7|x-4|\) เป็นลบเสมอ

สมมติเราต้องการหาเซตคำตอบของอสมการ \(\left|\dfrac{x-1}{x+1}\right|\gt2\) ที่เราค้างไว้ด้านบน แยกค่าสัมบูรณ์สักนิด

\(\require{cancel} \begin{aligned} \dfrac{|x-1|}{|x+1|}&\gt 2 \end{aligned}\)

เราคูณไขว้ขึ้นไปได้ เพราะ ตัวส่วนเป็นบวกเสมอเนื่องจากเป็นค่าสัมบูรณ์

\(\require{cancel} \begin{aligned} |x-1|&\gt 2|x+1| \end{aligned}\)

มาถึงขั้นตอนนี้ บางคนอาจสงสัยว่ารูปอสมการ ค่าสัมบูรณ์มันยังไม่ครอบเลข \(2\) จะยกกำลังสองได้เลยหรือเปล่า ได้เลยครับ เพราะ ถึงจะเอาเลข \(2\) ไปคูณก็เป็นบวกอยู่ดี ดังนั้น ทั้งสองฝั่งเป็นบวกยกกำลังสองได้เลย ไม่ต้องกลับเครื่องหมาย

\(\require{cancel} \begin{aligned} |x-1|^2&\gt (2|x+1|)^2\\ (x-1)^2&\gt 4(x+1)^2\\ x^2-2x+1&\gt 4(x^2+2x+1)\\ x^2-2x+1&\gt 4x^2+8x+4\\ 0&\gt 3x^2+10x+3\\ 0&\gt (3x+1)(x+3) \end{aligned}\)

นำเป็นเขียนเส้นจำนวน ที่เราเรียนใน เรื่อง การแก้อสมการพหุนาม

เราเลยได้ว่า คำตอบของอสมการคือ \(\left(-3,-\dfrac{1}{3}\right)\)

หาเซตคำตอบของ \(\left|\,x-\dfrac{3}{x}\right|\le2\)

เฉลย

ข้อนี้ดูเหมือนเป็นค่าสัมบูรณ์ฝั่งเดียว ตามรูปแบบที่ 1 แต่ถ้าลองทำจะเห็นว่าต้องแยกกรณีอีกอยู่ดี ดังนั้นวิธีการยกกำลังสองอาจจะเหมาะกว่า ลองจัดรูปกันสักนิด

\(\require{cancel} \begin{aligned} \left|\dfrac{x^2-3}{x}\right|&\le2\\ \dfrac{|x^2-3|}{|x|}&\le2 \end{aligned}\)

คูณไขว้ได้เลยเพราะส่วนเป็นบวก

\(\require{cancel} \begin{aligned} |x^2-3|&\le2|x| \end{aligned}\)

ข้อนี้สังเกตว่าถ้ากำลังสองเราจะได้กำลังสี่ ซึ่งปกติเราจะไม่ทำ แต่กำลังสี่ที่มีแค่พจน์ กำลังสี่ กำลังสอง และค่าคงที่ เราสามารถใช้ทริคแทน \(A=x^2\) ได้ ทำให้เหลือกำลังสอง ดังนั้น เราก็จะยกกำลังสองเพราะข้อนี้สามารถจัดรูปเหลือดีกรีกำลังสองได้

\(\require{cancel} \begin{aligned} (x^2-3)^2&\le(2|x|)^2\\ x^4-6x^2+9&\le4x^2\\ x^4-10x^2+9&\le0\\ A^2-10A+9&\le0\;\;\;,\;\;\;A=x^2\\ (A-9)(A-1)&\le0\\ (x^2-9)(x^2-1)&\le0\\ (x+3)(x-3)(x+1)(x-1)&\le0 \end{aligned}\)

ดังนั้นเราจะได้ว่าคำตอบคือ \((-3,-1)\cup(1,3)\)

หาเซตคำตอบของ \(|2x^2-5x-1|\le|x^2-x+4|\)

เฉลย

ข้อนี้ดูยังไงก็เป็นรูปแบบ 3 ที่เราต้องยกกำลังสองทั้งสองข้าง ซึ่งหากสังเกตุข้อนี้จะได้เป็นกำลังสี่แบบยาก แต่เราจะมีทริคให้สังเกตกัน ก่อนอื่นลองเขียนออกมาก่อน

\(\require{cancel} \begin{aligned} (2x^2-5x-1)^2&\le(x^2-x+4)^2 \end{aligned}\)

ถ้าเรากระจายกำลังสองเลยก็ได้ แต่จะได้กำลังสี่และเราต้องหารสังเคราะห์เพื่อแยกตัวประกอบ หลักการที่มักใช้กัน คือ ผลต่างกำลังสอง \(x^2-y^2=(x+y)(x-y)\)

\(\require{cancel} \begin{aligned} (2x^2-5x-1)^2-(x^2-x+4)^2&\le0\\ [(2x^2-5x-1)+(x^2-x+4)][(2x^2-5x-1)-(x^2-x+4)]&\le0\\ [3x^2-6x+3][x^2-4x-5]&\le0\\ 3(x^2-2x+1)(x-5)(x+1)&\le0\\ 3(x-1)^2(x-5)(x+1)&\le0\\ (x-1)^2(x-5)(x+1)&\le0 \end{aligned}\)

ตอบว่า \([-1,5]\)

เสริม ถ้าเราเจออสมการรูปแบบอื่น ๆ ที่ไม่สามารถทำเป็นรูปแบบทั้ง 3 ได้ เราสามารถกลับไปวิธีปกติ คือ แบ่งช่วงหาค่าวิกฤตเพื่อปลดล็อคอสมการ จากนั้น เราค่อยแก้ทีละอันแบบไม่ติดค่าสัมบูรณ์ได้เลย

หากบทความพี่เป็นประโยชน์ ฝากแชร์ต่อให้เพื่อนๆ ด้วยนะครับ :')