สมการค่าสัมบูรณ์ ม.4

เลือกอ่านตามหัวข้อ?

- เกริ่นค่าสัมบูรณ์

- สมการค่าสัมบูรณ์

\(|\square|=\heartsuit\)

ยกกำลังสองทั้งสมการ

เบสิค : แยกกรณีเป็นช่วง ๆ

อยากดูแบบวิดีโอ? (อยู่ระหว่างการจัดทำคลิป)

เกริ่นค่าสัมบูรณ์ (Absolute)

เราเรียนไปแล้วตอน ม.1 ว่า ค่าสัมบูรณ์คือการทำให้เป็นบวก แต่เรายังไม่ค่อยได้นำไปใช้อะไรมาก คือบทนี้เราจะมาดูว่า ไอ้เจ้าตัว ค่าสัมบูรณ์ ถ้ามันไปอยู่กับ สมการและอสมการ โดยเราจะเรียกว่า สมการค่าสัมบูรณ์ และ อสมการค่าสัมบูรณ์ มันจะต้องแก้สมการและอสมการยังไงให้เป็นระบบ (อสมการค่าสมบูรณ์ พี่ยกไปบทต่อไปนะ) ก่อนอื่นขอเกริ่น ทฤษฎีบท คร่าว ๆ

ในแต่ละข้อพี่ไม่อยากไห้น้องจำเลย แต่ให้น้องดูทีละอัน และพยายามคุยกับตัวเองว่า เราสามารถเข้าใจมัน แบบมันเมคเซ้นต์กับเราหรือเปล่า

เริ่มต้นด้วยบทนิยามของค่าสัมบูรณ์

\(\require{cancel}\begin{aligned} |a|=\begin{cases} \displaystyle a\;\;\;\;\;\,,\;\; a\ge 0\\ -a\;\;\;,\;\; a\lt 0 \end{cases} \end{aligned}\)

ห้ามจำนะ ข้างบนเป็นการเขียนที่แปลว่า ทำให้เป็นบวกนะ ลองดูเคสบน \(a\ge 0\) ก็แปลว่า \(a\) เป็นบวกอยู่แล้ว ก็เลยตอบ \(a\) ส่วนเคสล่าง เมื่อ \(a\lt 0\) แปลว่า ถ้า \(a\) ติดลบ เราต้องตอบเป็นบวกถูกไหม เราเลยใส่ลบไปให้มัน เช่น \(a=-5\) เราจะใส่ \(-(-5)\) หรือ \(-a\) นั่นเอง ลบเจอลบเป็นบวก ก็กลายเป็น \(5\) เห็นไหมว่ามันไม่ต้องจำ

\(\require{cancel}\begin{aligned} |x|=|-x| \end{aligned}\)

ในเมื่อค่าสัมบูรณ์คือการทำให้เป็นบวก เพราะงั้น \(x\) กับ \(-x\) ก็จะโดนตัดเครื่องหมายออก มันเลยเท่ากัน

\(|x|=|-x|=x\) ถูกต้องหรือไม่

เฉลย

\(\require{cancel}\begin{aligned} |xy|=|x||y| \\ \\\left|\dfrac{x}{y}\right|=\dfrac{|x|}{|y|}\;\;,\;\;y\ne 0 \end{aligned}\)

ข้อนี้คิดง่าย ๆ ว่า ฝั่งซ้ายเหมือนเราเอา \(x\) มาคูณ \(y\) แล้วสุดท้ายทำให้เป็นบวก แต่ฝั่งขวา ทำ \(x\) กับ \(y\) เป็นบวกก่อน แล้วค่อยมาคูณกัน มันเท่ากันเพราะว่า สุดท้ายฝั่งซ้ายก็เป็นบวก ฝั่งขวาก็บวก แค่ฝั่งขวาเราทำให้เป็นบวกก่อน แล้วค่อยคูณ ซึ่ง บวกคูณบวกได้บวก (หารก็คิดเหมือนกัน)

\(\require{cancel}\begin{aligned} |x-y|=|y-x| \end{aligned}\)

ข้อนี้ถ้าเรานึกถึงตอนเด็ก ๆ เวลานำตัวเลขลบกันมาสลับที่กัน เช่น \(2-5=-3\) กับ \(5-2=3\) เราจะได้ค่าเท่าเดิม แต่คนละเครื่องหมาย ทริคนี้เราชอบใช้กัน เวลาลบเลขตอนตัวหน้าน้อยกว่าตัวหลัง เช่นต้องการหา \(35-56\) เราจะคิดในใจว่าคำตอบเป็นลบนะ และคิด \(56-35=21\) แทน ดังนั้น \(35-56=-21\) ดังนั้นแปลว่า \(x-y\) กับ \(y-x\) มีค่าเท่ากันแบบไม่สนเครื่องหมาย ก็คือถ้าใส่ ค่าสัมบูรณ์มันจะมีค่าเท่ากัน นั่นเองครับ

\(\require{cancel}\begin{aligned} |x|^2=x^2 \end{aligned}\)

ฝั่งขวาการยกกำลังสองเป็นบวกเสมอถูกไหมเอ่ย ดังนั้นถ้าเราจะใส่ ค่าสัมบูรณ์ไปก่อนยกกำลังก็ไม่ผิดอะไร เพราะสุดท้ายคำตอบของกำลังสอง เป็นบวกอยู่แล้ว

\(\require{cancel}\begin{aligned} |x+y|\le|x|+|y| \end{aligned}\)

ข้อนี้ไม่ต้องจำ แต่อยากให้นึกถึงเสมอเวลาเจอค่าสัมบูรณ์ เพราะใช้บ่อยเหมือนกัน ข้อนี้ให้คิดแบบนี้สังเกตว่า การนำเลขสองตัวมาบวกกัน ถ้ามีตัวเลขตัวใดตัวหนึ่งเป็นลบ หรือทั้งสองตัว มันจะกลายเป็นการลบแทน (ค่าน้อยลง) แต่ฝั่งขวา เราทำให้ทุกตัวเป็นบวกก่อน ก่อนจะนำไปบวกกัน ดังนั้น ฝั่งขวามากกว่า (หรือเท่ากับ) ฝั่งซ้ายเสมอ เพราะฝั่งซ้ายอาจมีเลขลบมาหักออกได้

กรณีที่เท่ากันคือ \(x\) และ \(y\) เป็นบวกทั้งคู่
หรือ \(x\) และ \(y\) เป็นลบทั้งคู่

สมการค่าสัมบูรณ์

อยากจะบอกว่าหลักการทั้งในเรื่องอสมการด้วยนะ ให้น้องคิดแบบนี้ ค่าสัมบูรณ์เป็นคุก กล่าวคือ เราจะแก้สมการไม่ได้เลย ถ้ายังมีคนติดอยู่ในคุก ดังนั้น เราต้องปลกออกจากคุก โดยมี 2 กรณี สมมติ เรามี \(|\square|\) โดยการปลดออกจากคุกให้เราเปลี่ยน ค่าสัมบูรณ์ เป็น วงเล็บธรรมดา

ถ้า \(\square\) เป็นบวก (เป็นคนดี) เอาออกจากคุกได้เลย กลายเป็น \((\square)\)
ถ้า \(\square\) เป็นลบ (เป็นคนไม่ดี) เอาออกจากคุกได้ แต่ต้องติดลบมันไว้ (เป็นการติดทัณฑ์บนเอาไว้) กลายเป็น \(-(\square)\)

แต่โดยปกติแล้ว \(\square\) จะเป็นพหุนามที่ติดตัวแปร \(x\) ดังนั้น เราไม่มีทางรู้ว่า เป็นคนดีหรือคนไม่ดี (บางกรณีอาจรู้ถ้าโจทย์บอก หรือ มีข้อมูลเพิ่มเติม) ดังนั้น เราต้องแบ่งกรณีคิด (1) เป็นคนดี (2) เป็นคนไม่ดี ไปดูตัวอย่างกัน

จงหาค่า \(x\) เมื่อ \(|x-1|=3\)

\(x-1\) ติดคุกอยู่ เราเลยต้องแบ่งกรณี

กรณีแรก \(x-1\ge0\) เป็นบวก (คนดี)

แบบนี้เราจะปลดออกจากคุกได้เลย คือ \((x-1)=3\) อย่าลืมวงเล็บนะ ทำให้เป็นนิสัย เพราะโจทย์ถ้าซับซ้อนมากลืมวงเล็บอาจทำเครื่องหมายผิดได้

\(\require{cancel}\begin{aligned} (x-1)&=3 \\x&=4 \end{aligned}\)

แต่อย่าลืมว่าเรามีเงื่อนไขว่า \(x-1\ge0\) เป็นคนดีอยู่ ดังนั้น แก้สมการนิดหน่อยได้ว่า \(x\ge 1\) ซึ่ง \(x=4\) ไม่ได้ขัดแย้งอะไร เราเลยตอบได้ แสดงว่า กรณีแรก \(x=4\)

กรณีสอง \(x-1\lt0\) เป็นลบ (คนไม่ดี)

\(\require{cancel}\begin{aligned} -(x-1)&=3 \\-x+1&=3 \\x&=-2 \end{aligned}\)

กรณีคนไม่ดี คือ \(x-1\lt 0\) แปลว่า \(x\lt0\) เพราะฉะนั้น เราเลยได้ว่า ไม่ขัดแย้ง ดังนั้น \(x=-2\) เป็นอีกคำตอบของสมการ

ตอบ เซตคำตอบคือ \(\{-2,4\}\)

ทริคถ้าเจอรูปแบบ \(|\square|=\heartsuit\)

จริง ๆ ถ้าเราเจอโจทย์รูปแบบนี้ เราไม่ต้องแยกกรณีก็ได้ ลองคิดดี ๆ การที่ \(\square\) ใส่ค่าสัมบูรณ์ แล้วมีค่าเท่ากับ \(\heartsuit\) แปลว่า \(\square\) เป็นได้ 2 กรณี คือ \(\square=\heartsuit\) หรือ \(\square=-\heartsuit\)

ดังนั้น ข้อนี้ \(|x-1|=3\) หมายความว่า \(x-1=3\) หรือ \(x-1=-3\) แก้ได้ \(x=4,-2\) ตามที่เราคิดเลย

ข้อควรระวัง เราต้องเช็คคำตอบด้วยเมื่อได้ \(x\) มาโดย \(\heartsuit\ge 0\) เสมอ เพราะ \(\heartsuit\) เป็นคำตอบ ที่มาจากค่าสัมบูรณ์ของฝั่งซ้าย ดังนั้น มันเป็นบวกเสมอ

หาเซตคำตอบของ \(|x-1|=3-x\)

เฉลย

หาเซตคำตอบของ \(|x^2+x-2|=x^2-4x+3\)

เฉลย

หาเซตคำตอบของ \(|x-1|=2x-3\)

เฉลย

ทริคการยกกำลังสองทั้งสองข้างเพื่อกำจัดค่าสัมบูรณ์

ทริคนี้เป็นทริคที่ใช้บ่อยเช่นกัน ในการยกกำลังสองทั้งสองข้าง ทำไมถึงทำได้ เพราะว่า การยกกำลังสองทำให้เป็นบวกนั่นเอง ดังนั้น หากเรามี \(|x|\) เราไม่รู้ว่า \(x\) เป็นบวกหรือลบ แต่สุดท้าย \(x^2\) เป็นบวกเสมอ ดังนั้น \(|x|^2=x^2\) นั่นเอง (ทฤษฎีบทที่เราเรียนไปตอนช่วงแรก)

การยกกำลังสอง อาจทำให้คำตอบของสมการเพิ่มขึ้น อย่างเช่น สมมติ เราบอกว่า \(x=2\) มีคำตอบเดียว แต่พอยกกำลังสอง \(x^2=4\) จะได้ว่าสมการนี้มีสองคำตอบ คือ \(-2, 2\) ดังนั้น การใช้ทริคยกกำลังสอง ต้องตรวจทุกคำตอบทุกครั้ง

อีกข้อสังเกต เวลาทำโจทย์ ถ้าเราใช้ทริคยกกำลังสอง โจทย์ 99% จะไม่ให้น้องแก้สมการยกกำลังเกินดีกรี \(2\) ถ้าน้องทำโจทย์แล้ว น้องจะยกกำลังสองจนมันกลายเป็นติดดีกรีกำลังสี่ ให้ลองมองหาวิธีอื่นก่อน อย่าพึ่งไปทำให้เป็นกำลังสี่นะ เพราะมันแยกตัวประกอบยาก ให้กลับไปสู่เบสิคที่ว่า แทนเป็นคนดีคนไม่ดี แยกกรณี

สมมติว่าเราเจอโจทย์ถามว่า \(x^2+4=4|x|\)

มันไม่อยู่ในรูป \(|\square|=\heartsuit\) และถ้ากำลังสองก็จะได้ ฝั่งซ้ายก็จะได้กำลังสี่ ดังนั้น เราจึงลองกลับไปสู่เบสิคก่อน มี \(x\) ติดคุกอยู่ แบ่งกรณีเป็น

กรณี 1 \(x\ge0\)

\(\require{cancel}\begin{aligned} x^2+4&=4(x) \\x^2-4x+4&=0 \\(x-2)^2&=0 \\x&=2 \end{aligned}\)

ซึ่งไม่ขัดแย้งกับ \(x\ge0\) ดังนั้น \(x=2\) เป็นคำตอบ

กรณี 2 \(x\lt0\)

\(\require{cancel}\begin{aligned} x^2+4&=4(-(x)) \\x^2+4&=-4x \\x^2+4x+4&= \\(x+2)^2&=0 \\x&=-2 \end{aligned}\)

ซึ่งไม่ขัดแย้งกับ \(x\lt0\) ดังนั้น \(x=-2\) เป็นคำตอบ

ข้อนี้จึงตอบว่า เซตคำตอบ คือ \(\{-2,2\}\)

เสริม (1) ข้อนี้จัดรูปแบบนี้ได้ \(\dfrac{x^2+4}{4}=|x|\) จะเข้าสู่สูตรแบบแรก \(|\square|=\heartsuit\) เราก็แก้โดยแยกเป็น \(x=\dfrac{x^2+4}{4}\to x=2\) และ \(x=-\dfrac{x^2+4}{4}\to x=-2\) นำสองคำตอบไปเช็คว่า \(\dfrac{x^2+4}{4}\ge0\) ซึ่งทั้งคู่ใช้ได้ ตอบ \(\{-2,2\}\)

เสริม (2) ข้อนี้ยกกำลังสองก็ได้ ถึงจะติดกำลังสี่ แต่มันมีแค่กำลังสี่ กำลังสอง และกำลังศูนย์ (3 พจน์) ดังนั้น เราใช้ทริคแทน \(A=x^2\) ได้เพื่อให้เหลือกำลังดีกรีสอง ประมาณนี้

\(\require{cancel}\begin{aligned} (x^2+4)^2&=(4|x|)^2 \\x^4+8x^2+16&=16x^2 \\x^4-8x^2+16&=0 \\A^2-8A+16&=0\;\;\;\;\;\;\;,\;\; A=x^2 \\(A-4)^2&=0 \\A&=4 \\x^2&=4\;\;\;\;\;\;\;,\;\;A=x^2 \\x&=-2, 2 \end{aligned}\)

นำไปเช็คในสมการ ได้ว่าใช้ได้ทั้งหมด ก็ตอบเหมือนกันว่า \(\{-2,2\}\)

ที่พี่ยกข้อนี้มา เพราะ อยากจะบอกน้อง ๆ ว่า การแก้สมการอสมการพหุนาม สามารถทำได้หลากหลายแบบมาก แล้วแต่ว่าน้องจะมองโจทย์ยังไง แต่คำตอบสุดท้ายยังไงก็จะเท่ากัน เพราะฉะนั้น เรื่องนี้ยิ่งฝึกเยอะเท่าไหร่ ยิ่งคล่องกับตัวเราเองเท่านั้นครับ พี่ทำได้แค่จัดหมวดหมู่ ว่าสมการมีรูปร่างประมาณไหนบ้าง สุดท้ายอยู่ที่ตัวน้องเองแล้ว ว่าจะฝึกโจทย์กันต่อเยอะขนาดไหน อ่ะไปต่อ

หาเซตคำตอบของ \(|x-1|=|2x+1|\)

เฉลย

ข้อนี้สังเกตว่า มีค่าสัมบูรณ์ทั้งสองข้าง วิธีเบสิคคือแยกช่วงคิด แต่เนื่องจากต้องแยกเยอะเพราะมันสองตัว พี่จะจับยกกำลังสอง แล้วเช็คคำตอบสมการดีกว่า

\(\require{cancel}\begin{aligned} |x-1|^2&=|2x+1|^2 \\(x-1)^2&=(2x+1)^2 \\x^2-2x+1&=4x^2+4x+1 \\0&=3x^2+6x \\0&=3x(x+2) \\x&=-2,0 \end{aligned}\)

นำไปแทนในสมการเริ่มต้น

เมื่อ \(x=0\) จะได้ \(|0-1|=1\) และ \(|2(0)+1|=1\) ดังนั้น ใช้ได้

เมื่อ \(x=-2\) จะได้ \(|-2-1|=3\) และ \(|2(-2)+1|=3\) ดังนั้น ใช้ได้

เซตคำตอบจึงได้ \(\{-2,0\}\)

หมายเหตุ : ถ้าสังเกตดี ๆ การที่ทั้งสองด้านติด ค่าสัมบูรณ์และเรายกกำลังสอง จริง ๆ ไม่ต้องตรวจคำตอบก็ได้ เพราะสุดท้ายแทนเข้าไป ค่าก็จะได้เท่ากัน แค่มีโอกาสคนละเครื่องหมาย แต่ในเมื่อสมการใส่ ค่าสัมบูรณ์ให้ทั้งสองด้าน ก็แปลว่า มันจะเท่ากันเสมอ แต่พี่แนะนำถ้าใครยังรู้สึกงง ๆ ว่าอันไหนต้องเช็คคำตอบ อันไหนไม่ต้องเช็ค ก็สามารถเช็คเร็ว ๆ ทุกข้อแหละ เพื่อความชัวร์

หาเซตคำตอบของ \(2|x+3|=|x-2|\)

เฉลย

กลับสู่เบสิค : การแบ่งกรณีคนดีคนไม่ดี

สุดท้ายแล้วถ้าทริคด้านบนไม่เวิร์คเอาซะเลย เราก็จะกลับไปทำวิธีปกติ คือ แบ่งกรณี และปลดออกจากคุก คำถาม คือ แล้วเราจะแบ่งกรณียังไง หากมีหลายคุก หรือ ติดสัมบูรณ์หลายตัว

วิธีการที่พี่แนะนำ คือ ให้แบ่งกรณีรวมกัน อย่าคิดแยกว่า

ถ้าคุก 1 คนดี คุก 2 คนดี
ถ้าคุก 1 คนดี คุก 2 คนไม่ดี
ถ้าคุก 1 คนไม่ดี คุก 2 คนดี
ถ้าคุก 1 คนไม่ดี คุก 2 คนไม่ดี

เพราะถ้ามีหลาย \(n\) คุก น้องจะได้ \(2^n\) กรณีซึ่งเยอะแยะมาก และบางกรณีก็เป็นไปไม่ได้ด้วย ดังนั้น ทริคคือ ให้เราเขียนเส้นจำนวนขึ้นมาครับ และนำค่าวิกฤต (ตอนที่คนในคุกเป็น 0 หรือเป็นจุดเปลี่ยนคนดี-คนไม่ดีพอดี) มาเขียนในเส้นจำนวน จากนั้นใช้ช่วงที่โดนแบ่งในเส้นจำนวนนั่นแหละคิด

ไปดูตัวอย่างกันครับ

สมมติมีโจทย์ว่า \(|x|+|2x-4|=|x+1|\)

น้องรู้ใช้ไหมครับว่า การยกกำลังสองสมการนี้ยังไม่ทำให้ค่าสัมบูรณ์หายไป เพราะตัวหน้ามันจะเข้าสูตร \((x+y)^2=x^2+2xy+y^2\)

\(\require{cancel}\begin{aligned} (|x|+|2x-4|)^2&=|x+1|^2 \\(x)^2+2|x||2x-4|+(2x-4)^2&=x^2+2x+1 \\\dots \end{aligned}\)

ยังติดค่าสัมบูรณ์อยู่พจน์กลาง \(2|x(2x-4)|\) ต้องแก้โดยย้ายทุกอย่างไปฝั่งขวาเหลือแค่ค่าสัมบูรณ์ไว้ฝั่งซ้าย และยกกำลังสองอีกรอบ ซึ่งจะทำให้เป็นกำลังสี่ ทำได้แต่เยอะ

ดังนั้น ข้อนี้เราจะแยกกรณีกัน ก่อนอื่นนำค่าวิกฤตมาเรียง จะได้ว่า \(-1, 0, 2\) (จับแต่ละตัวเท่ากับ 0 นะ เช่น \(2x-4=0\))

ตรงจุดแบ่งช่วงค่าวิกฤต เราจะนำไปไว้ฝั่งไหนก็ได้นะ อย่างเช่น \(-1\) พี่ให้ไปอยู่กรณี 2 แต่น้องอยากให้อยู่ฝั่งซ้ายก็ได้ แต่ทำให้มันเหมือนกัน ถ้าน้องจะโยน ค่าวิกฤตไปฝั่งขวา ก็ให้ไปฝั่งขวาให้หมด

ในแต่ละช่วง เราจะคิดว่าแต่ละคุก เป็นคนดีหรือคนไม่ดี เวลาเราคิดกรณีนั้น ๆ จะได้รู้ว่าเวลาปลดต้องใส่เครื่องหมายลบติดด้วยหรือเปล่า วิธีการง่าย ๆ คือการแอบหยิบสักตัวเลขในช่วงนั้นมาแทนค่าดู เช่น กรณีที่ 2 พี่จะหยิบ \(-0.5\) มาแทน (อย่าหยิบค่าวิกฤตมาแทนนะ เพราะมันจะมีวงเล็บนึงเป็น \(0\) เราจะงงว่าสรุปแล้วเป็นคนดีหรือไม่ดี ดังนั้น หยิบเลขตรงอื่นในช่วงมาแทนดีที่สุด) ได้ว่า

\(|x|\) จะได้ว่าตัวในคุก \(x\) เป็นคนไม่ดี เพราะ \(x=-0.5\) ติดลบ ดังนั้น ก้อนนี้กรณี 2 เราจะปลดโดยใส่ลบ
\(|2x+4|\) จะได้ว่าตัวในคุก \(2x-4\) เป็นคนดี เพราะ \(2x+4=2(-0.5)-4=-5\) เป็นลบ ดังนั้น ก้อนนี้กรณี 2 เราจะปลดโดยใส่ลบ
\(|x+1|\) จะได้ว่าตัวในคุก \(x+1\) เป็นคนดี เพราะ \(x+1=0.5\) เป็นบวก ดังนั้น ก้อนนี้กรณี 2 เราจะปลดได้เลย

สมการในกรณี 2 เราก็จะได้ \(-(x)+-(2x-4)=(x+1)\)

เราจะทำแบบนี้ทุกกรณี เพื่อสร้างสมการ ได้ดังนี้ (หลักการคือ แต่ละคุกจะมีค่าวิกฤตของมันอยู่ ดังนั้น ฝั่งนึงของค่าวิกฤตจะเป็นบวก แล้วอีกฝั่งจะเป็นอีกเครื่องหมาย คือ ลบ)

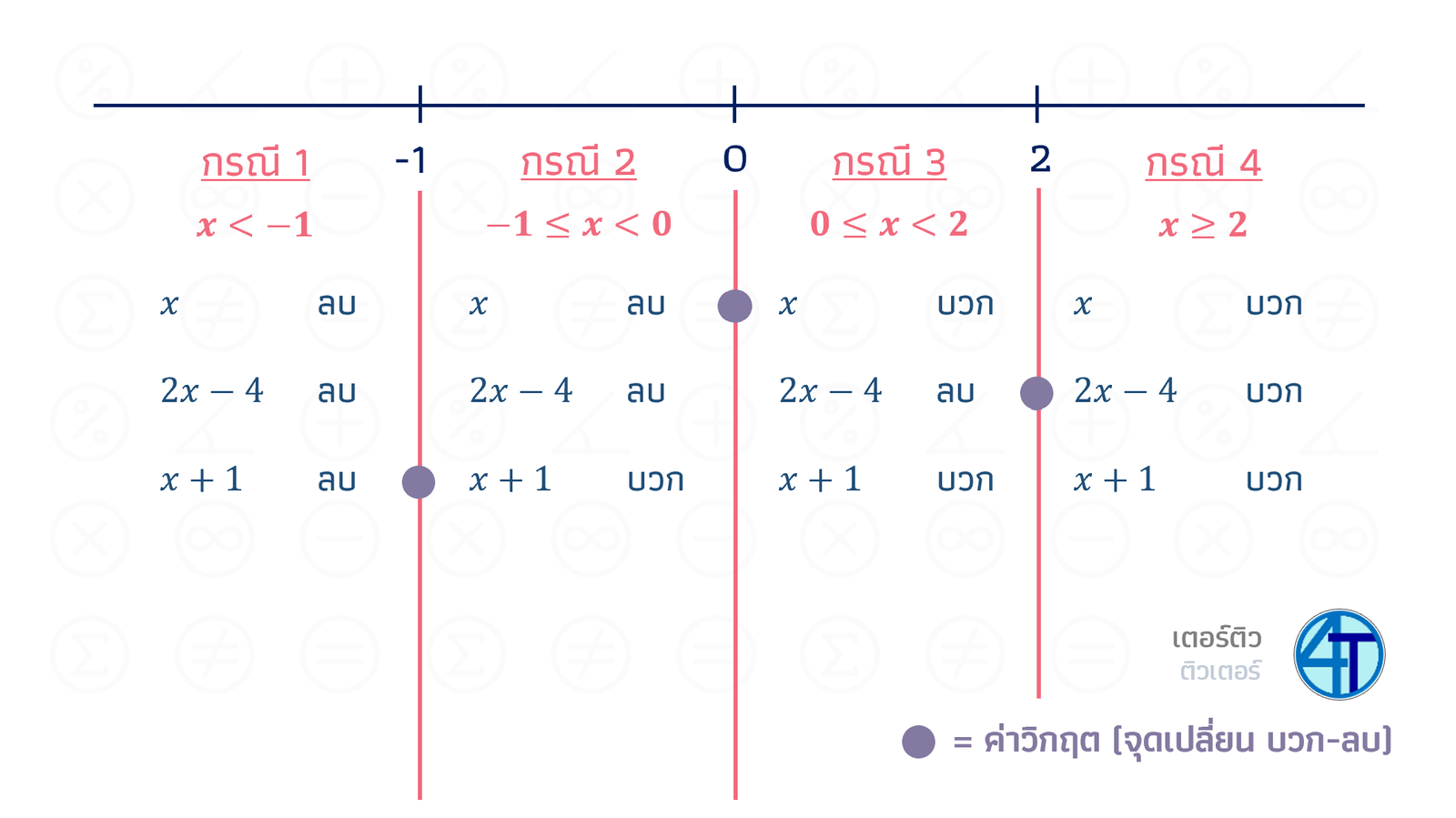
พอเราได้แล้วว่าแต่ละกรณี แต่ละก้อน (คุก) เป็นบวกหรือลบ เราก็จะปลดได้ โดยคิดสมการได้ตามนี้

กรณีที่ 1 \(-(x)+-(2x-4)=-(x+1)\)

\(\require{cancel}\begin{aligned} -x-(2x-4)&=-x-1 \\-x-2x+4&=-x-1 \\2x&=5 \\x&=\dfrac{5}{2} \end{aligned}\)

ขัดแย้งกับช่วงกรณี 1 ที่ว่า \(x\lt -1\) ดังนั้น ช่วงนี้ไม่มีคำตอบ

กรณีที่ 2 \(-(x)+-(2x-4)=(x+1)\)

\(\require{cancel}\begin{aligned} -x-(2x-4)&=x+1 \\-x-2x+4&=x+1 \\3&=4x \\x&=\dfrac{3}{4} \end{aligned}\)

ขัดแย้งกับช่วงกรณี 2 ที่ว่า \(-1\le x\lt0\) ดังนั้น ช่วงนี้ไม่มีคำตอบ

กรณีที่ 3 \((x)+-(2x-4)=(x+1)\)

\(\require{cancel}\begin{aligned} x-(2x-4)&=x+1 \\x-2x+4&=x+1 \\3&=2x \\x&=\dfrac{3}{2} \end{aligned}\)

อยู่ในช่วงกรณี 3 พอดี ดังนั้น กรณี 3 มี \(x=\dfrac{3}{2}\) เป็นคำตอบ

กรณีที่ 4 \((x)+(2x-4)=(x+1)\)

\(\require{cancel}\begin{aligned} 3x-4&=x+1 \\2x&=5 \\x&=\dfrac{5}{2} \end{aligned}\)

ไม่ขัดแย้ง เพราะ กรณี 4 บอกว่า \(x\ge 2\) ดังนั้น กรณี 4 มี \(x=\dfrac{5}{2}\) เป็นคำตอบ

เราเลยได้ว่า คำตอบสมการนี้คือ \(\left\{\dfrac{3}{2},\dfrac{5}{2}\right\}\)

น้องอาจจะคิดว่ามันดูเยอะนะ แต่การแบ่งช่วงไม่ยากและสังเกตพอแบ่งเสร็จ เราได้สมการเชิงเส้นตัวแปรเดียว แบบแก้ง่ายมาก ๆ ดังนั้น มันไปหนักที่การหาค่าวิกฤตแบ่งช่วงมากกว่า การแก้สมการด้วยซ้ำ

หากบทความพี่เป็นประโยชน์ ฝากแชร์ต่อให้เพื่อนๆ ด้วยนะครับ :')