เลือกอ่านตามหัวข้อ?
เกริ่นนำ : เข้าใจคำว่าอสมการ อสมการคืออะไร
ถ้าน้อง ๆ จำได้ ในบทเรียน ม.1 เราเรียนเรื่อง สมการเชิงเส้นตัวแปรเดียว กันเอาไว้ด้วย หน้าตามันจะประมาณ \(x+4=10\) หลักการที่เราใช้ก็คือ นำ 4 ไปลบออกทั้งสองข้าง \(x+4\textcolor{blue}{-4}=10\textcolor{blue}{-4}\) ฝั่งซ้าย \(4\) เลยตัดกันทิ้ง เหลือเป็น \(x=10-4=6\) ดังนั้น เราก็ได้และว่าคำตอบสมการ \(x\) คือ \(6\)
พี่อยากให้น้อง ๆ สังเกตกันดี ๆ ตรงเครื่องหมาย \(=\) (เท่ากับ) นี่แหละครับที่เป็นเหตุผลว่า ทำไมเราเรียกมันว่า สมการ เพราะ สมการ คือ ประโยคสัญลักษณ์ที่มีเครื่องหมาย = แสดงความเท่ากันทั้ง 2 ข้าง
ดังนั้น ในเรื่อง อสมการ คำว่า "อ-" หากจำได้ มันเหมือนในเรื่อง "อ-ตรรกยะ" เลยน้อง "อ-" แปลว่า ไม่ ไม่ใช่ ไม่ใช่นะ อะไรประมาณนี้ ดังนั้น อสมการ ก็คือ เป็นสมการแหละ แต่เครื่องหมาย ไม่ใช่ = และ หรือพูดอีกอย่างนึงว่า มันคือสมการไม่ได้แสดงความเท่ากัน
ดัวอย่างเช่น \(x>5\) (อ่านว่า \(x\) มากกว่า 5) หรือ \(x-3\leq 7\) (อ่านว่า \(x\) ลบสาม น้อยกว่าหรือเท่ากับ 7)
ดังนั้น อสมการ คือการแสดงความไม่เท่ากันของสิ่งของสองฝั่ง ซึ่งเราก็จะมีเครื่องหมายต่าง ๆ ไว้ใช้แทน เช่น \(\gt\) คือ มากกว่า เป็นต้น ในพาร์ทต่อไป เราจะไปดูกันว่าเครื่องหมายมีอะไรบ้าง
เครื่องหมายในอสมการ

เครื่องหมายด้านบน ก็คือเครื่องหมายแทน น้อยกว่า หรือ มากกว่า ตั่งต่าง ที่น่าสนใจคือ เวลาเราเจอโจทย์ เราจะสามารถแปลงจาก ประโยคทั่วไปปกติ เป็น อสมการที่เป็นเครื่องหมายทางคณิตศาสตร์ ได้หรือเปล่า ตัวอย่างเช่น "สามเท่าของเลขจำนวนหนึ่งไม่เกิน 18" สิ่งที่เราต้องทำคือ เลขจำนวนหนึ่งให้แทนเป็นตัวแปร ที่เราคุ้น ใช้ \(x\) ก็ได้ ดังนั้น สามเท่าของ \(x\) ไม่เกิน 18 เราก็จะได้ว่า \(3x\) ไม่เกิน 18 ตัวคำว่า ไม่เกิน นี่แหละครับน้อง ๆ ที่จะมักสับสน หากเราวิเคราะห์ดี ๆ การ ไม่เกิน 18 แปลว่า มันน้อยกว่า 18 แต่ก็เท่ากับ 18 ได้ด้วย (18 ไม่เกิน 18) ดังนั้น เราต้องใช้สัญลักษณ์ \(\leq\) นั่นเอง
"สามเท่าของเลขจำนวนหนึ่งไม่เกิน 18" คือ \(3x\leq 18\)
ลองฝึกแปลงประโยคเป็นอสมการก่อนตามตัวอย่างโจทย์ด้านล่างกันเลย
ดังนั้น หากน้อง ๆ ชินกับการแปลงประโยคเป็นอสมการแล้ว เรื่องต่อไปที่เราต้องเรียนก็คือ การแก้อสมการนั่นเอง
คำตอบของอสมการ
ในเรื่อง สมการ หากน้องจำได้ เราจะได้คำตอบเป็น \(x=\) ตัวเลขอะไรสักอย่าง เช่น \(x=1\) หรือ \(x=-10\) แต่คำตอบของอสมการ จะมีความแตกต่างไป เพราะเครื่องหมายตรงกลาง ไม่ใช่เท่ากับ แต่เป็น มากกว่า น้อยกว่า ดังนั้น สมมติเราเปลี่ยนคำตอบด้านบนเป็น \(x\gt1\) หรือ \(x\lt-10\)
\(x\gt1\) หมายความว่าคำตอบคือ จำนวนจริงใด ๆ ทุกตัวที่มากกว่า 1 เช่น \(x\) จะเป็น \(2\) ก็ย่อมได้ หรือ \(3,4,5,\dots\) และจริง ๆ มันไม่จำเป็นต้องเป็นจำนวนเต็มนะ เช่น \(x\) คือ \(1.00001\) ก็มากกว่า \(1\) ตามเงื่อนไขแล้วจริงมั้ย ดังนั้น คำตอบอสมการจึงเยอะมาก นับไม่ถ้วน
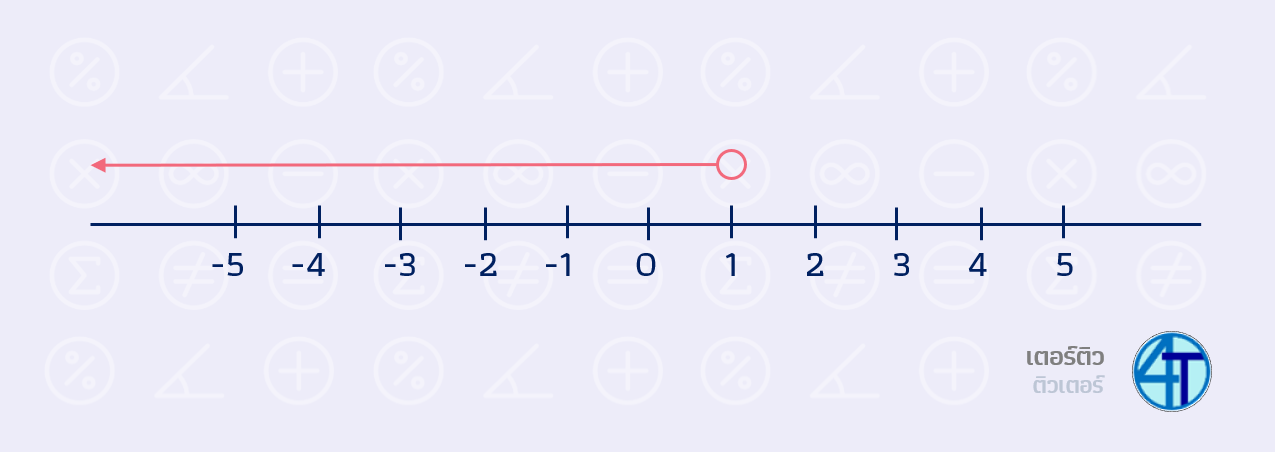
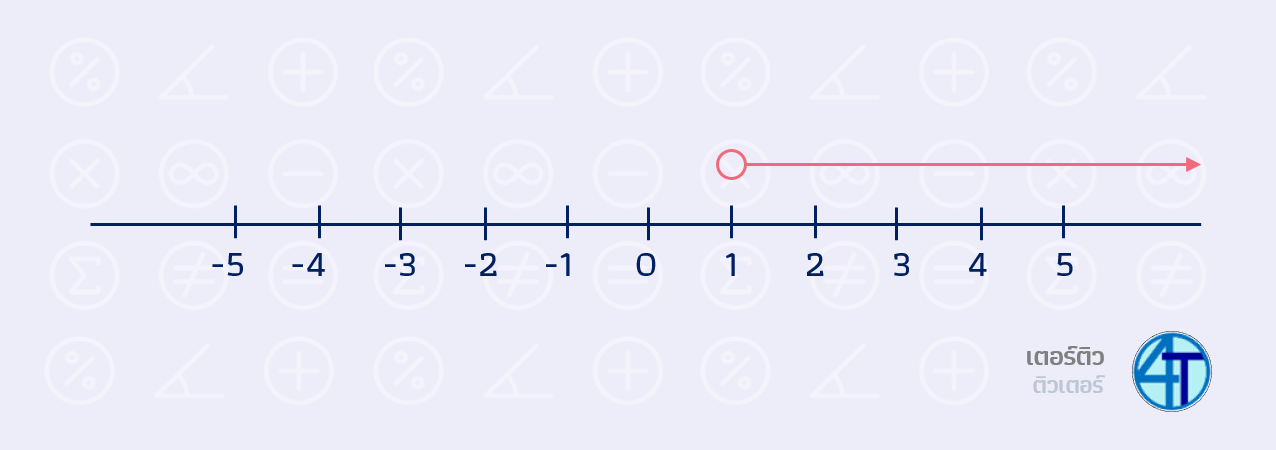
เราเลยมีสัญลักษณ์เพิ่มเติม ว่า หากเราได้คำตอบมาแล้ว เช่นคำตอบคือ \(x\gt1\) เราจะเขียนมันบนเส้นจำนวนแบบนี้
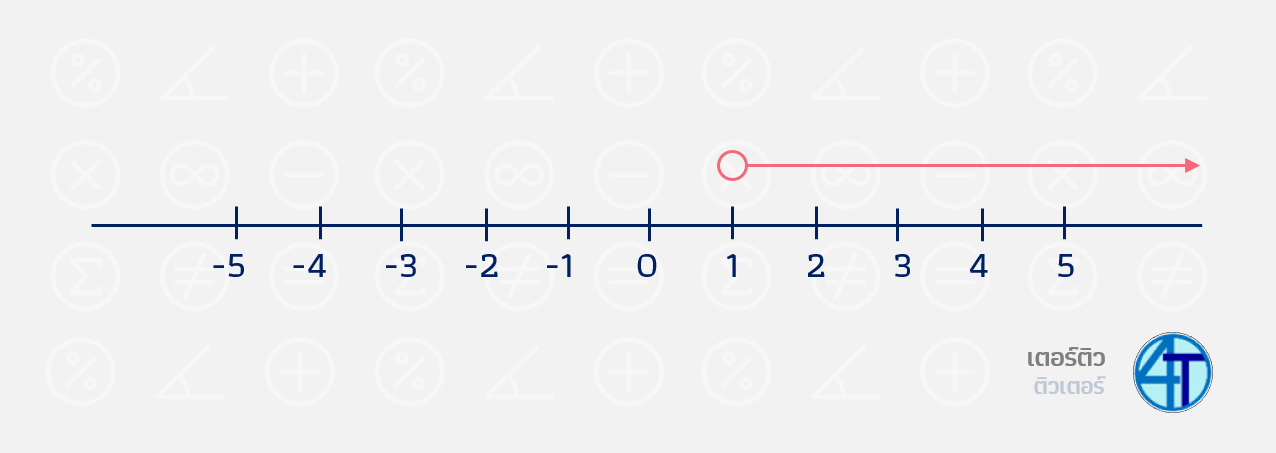
ก็คือเริ่มที่จุดตรงเลข 1 และมากกว่าเป็นลูกศรลากไปทางขวา (เอาหมดที่อยู่ด้านขวานั่นเอง)
แล้วถ้าหากเรามีคำตอบ \(x\geq1\) ล่ะ มันต่างจากอันข้างบน แค่ \(x\) เป็น \(1\) ได้ด้วย แค่นั้นเอง เพราะอันบนคือ \(x\gt1\) ซึ่งก็คือมากกว่า 1 แต่ \(x\geq1\) คือมากกว่าหรือเท่ากับ \(1\) เนื่องจากช่วงมันเหมือนกัน แต่อันนึงเอา \(1\) อีกอันไม่เอา \(1\)
เราเลยมีสัญลักษณ์ สองตัวเพิ่มขึ้นมา คือ จุดโปร่ง กับ จุดทึบ หากน้องสังเกตรูปด้านบน พี่วงกลมตรงเลข \(1\) ไว้ใหญ่มากและ ไม่ระบายสิใด ๆ = จุดโปร่ง ซึ่งหมายความว่า ไม่เอา 1 นะ ดังนั้น หากพี่ต้องการเขียนตอบ \(x\geq1\) เราก็ต้องใช้จุดทึบดังรูปด้านล่างนี้ เมื่อน้องนำมาเปรียบเทียบกันจะเห็นความต่างชัดเจน

จุดโปร่ง = ไม่เอาตัวนั้น
จุดทึบ = เอาตัวนั้น
การแก้อสมการ
การแก้อสมการ เหมือนกับ การแก้สมการเลยครับน้อง ๆ แต่ จะมีข้อระวังบางอย่าง ที่เดี๋ยวเราจะมาดูไปด้วยกันว่า การแก้อสมการเชิงเส้นตัวแปรเดียว เนี่ย มีอะไรบ้างที่ต้องระวัง

หากยังจำกันได้ ด้านบนเป็น การแก้สมการขั้นพื้นฐาน ม.1 โดยเราจะทำการย้ายข้าง คือ เอาตัวแปรไปไว้ด้านเดียวกัน และตัวเลขตบไปด้านทีเหลือ ซึ่งหากเราย้ายข้าง เราก็ต้องกลับเครื่องด้วย ตามนี้
บวกเป็นลบ / ลบเป็นบวก
คูณเป็นหาร / หารเป็นคูณ
ดังนั้นในเรื่องอสมการก็เหมือนกันครับน้อง ๆ ย้ายข้างกลับเครื่องหมาย แต่! หากน้องทำการย้ายข้าง จำนวนติดลบ แบบคูณ/หาร น้อง ๆ ต้องจำไว้เสมอว่า ต้องกลับเครื่องหมายอสมการ
ทำไมย้ายจำนวนลบ (คูณหาร) ต้องกลับเครื่องหมาย?
ลองดูตัวอย่างอสมการเชิงเส้นตัวแปรเดียว สมมติ พี่บอกว่า \(-2\times5\gt-20\) ซึ่งเป็นจริงถูกมั้ยครับ \(-2\times5\) ได้ \(-10\) ซึ่งมากกว่า \(-20\) หากน้อง ลองจับ \(-2\) จากคูณไปหาร จะได้แบบนี้ \(5\gt\dfrac{-20}{-2}\) ซึ่งอสมการนี้กลายเป็นเท็จเฉยเลย เพราะ ฝั่งซ้ายคือ \(5\) แต่ฝั่งขวาคือ \(\dfrac{-20}{-2}=10\) และ ซึ่ง \(5\) มันมากกว่าสอบซะที่ไหนกัน
ดังนั้น เราต้องกลับเครื่องหมาย อสมการ จาก \(\gt\) เป็น \(\lt\) นั่นเอง
ดังนั้น หลักการคร่าว ๆ ก็คือหากน้อง ๆ ย้ายเลขลบแบบคูณหารเมื่อไหร่ ตระหนักไว้เลยว่าต้องกลับเครื่องหมาย การกลับก็แค่กลับด้านครับ
\(\gt\;\rightarrow\;\lt\) หรือ \(\geq\;\rightarrow\;\leq\)
\(\lt\;\rightarrow\;\gt\) หรือ \(\leq\;\rightarrow\;\geq\)
ตัวอย่างโจทย์ สมมติ พี่มี \(x-4\gt6\) เราก็ทำได้ย้ายตัวเลขไปฝั่งเดียวกันให้หมด โดยย้าย \(4\) ไป จาก ลบเป็นบวก ดังนั้น \(x\gt6+4\) ซึ่งได้ว่า \(x\gt10\) เราก็ตอบว่าคำตอบของอสมการนี้คือ \(x\gt10\) (หรือ พูดว่า จำนวนใด ๆ ที่มากกว่า 10)
เขียนอันข้างบนแบบเข้าใจง่าย ๆ ได้ดังนี้
\( \begin{align} x-4& \gt6 \\[5pt] x& \gt6+4 \\[5pt] x& \gt10 \\ \end{align} \)
เราก็จะเขียนคำตอบในเส้นจำนวนได้แบบนี้ เพราะ \(x\) มากกว่า \(10\) ตรงเลข \(10\) เลยต้องเป็นจุดโปร่ง
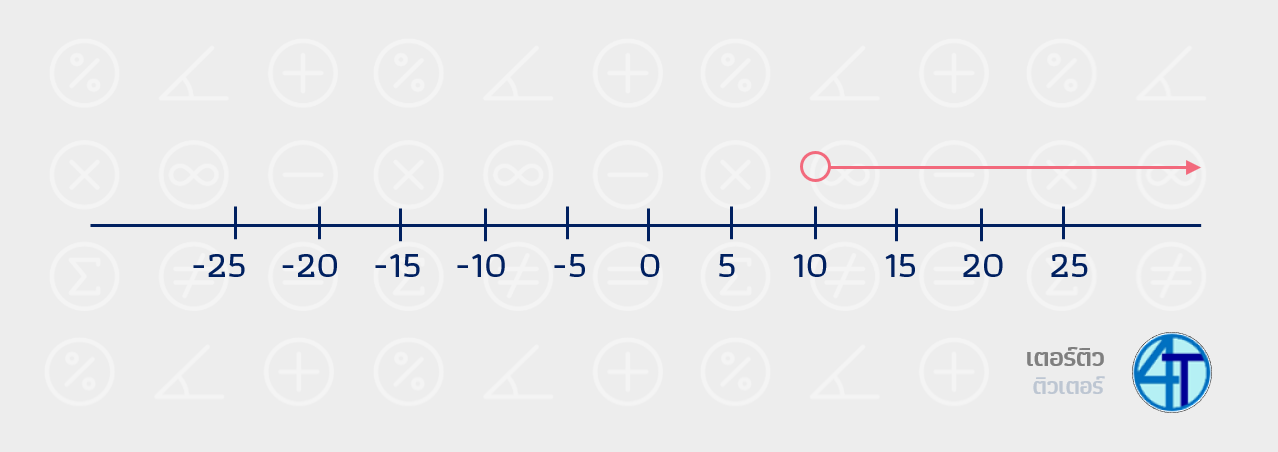
หากน้องเริ่มเข้าใจหลักการกันแล้ว ลองมาฝึกทำโจทย์ปัญหาอสมการเชิงเส้นตัวแปรเดียว ด้านล่างกันครับ
หากบทความพี่เป็นประโยชน์ ฝากแชร์ต่อให้เพื่อนๆ ด้วยนะครับ :')