การแยกตัวประกอบของพหุนามดีกรีสอง ม.2

เข้าใจหลักการแยกตัวประกอบ สองวงเล็บ

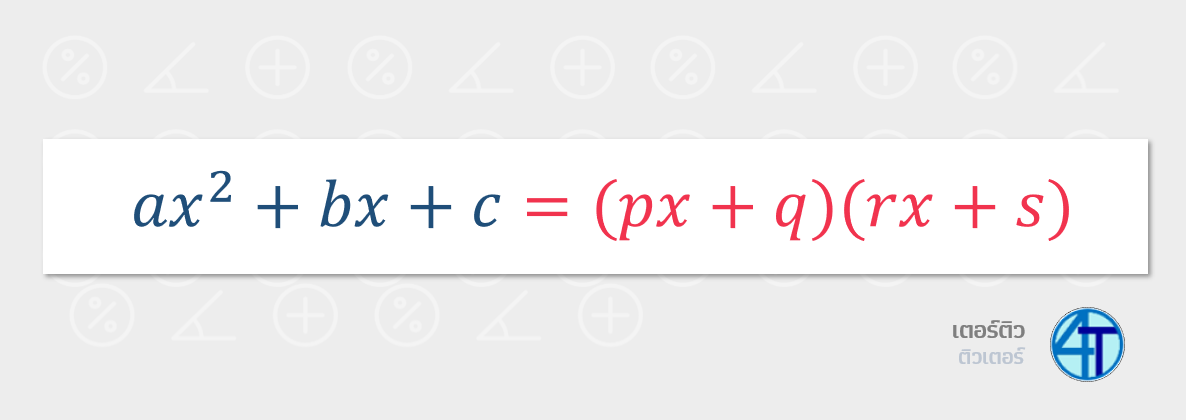
อย่าพึ่งไปสนใจภาพข้างบนมากนะครับน้อง ๆ มันเป็นแค่ไอเดียเฉย ๆ ที่พี่อยากให้โฟกัสคือ ในเรื่องนี้เราจะเน้นไปที่ สมการ ตัวแปรเดียว ซึ่งก็คือ ตัวแปร x และกำลังสูงสุดคือ กำลังสอง ในพจน์ \(x^2\) นั่นเอง

ในแต่ละพจน์น้องก็จะมี สัมประสิทธิ์หน้าพจน์ หากสังเกตจากรูปด้านบน ก็จะเห็นว่า มีทั้งหมด 3 พจน์ ซึ่งก็น่าจะพอมองกันออกเนอะว่า พหุนามดีกรีสองเนี่ย มันจะมี (1) พจน์ดีกรีสอง \(x^2\) (2) พจน์ดีกรีหนึ่ง \(x^1=x\) และ (3) พจน์ดีกรีศูนย์ หรือ \(x^0=1\) ซึ่งเป็นพจน์ที่ไม่มี \(x\) นั่นเอง เพราะดีกรีศูนย์ก็จะทำให้ \(x\) หายไป

ดังนั้นการแยกตัวประกอบพหุนาม ก็ไม่ต่างอะไรไปจาก การแยกตัวประกอบ ตัวเลขปกติที่น้อง ๆ เคยเรียนตอนชั้นประถมเลย เช่น \(12=2\times2\times3\) สังเกตว่ามันคือหาตัวเลขมาคูณกัน

ในเรื่อง การแยกตัวประกอบพหุนาม ก็หนีไม่พ้นการหา "อะไรมาคูณกัน" กลับไปดูที่รูปด้านบน น้องจะเห็นว่า เราก็จะแยกได้สองวงเล็บ วงเล็บแต่ละอัน มีแค่ x ดีกรีหนึ่ง เพราะหากเราคูณกลับก็จะได้ ดีกรี 2 นั่นเอง ตามภาพด้านล่าง

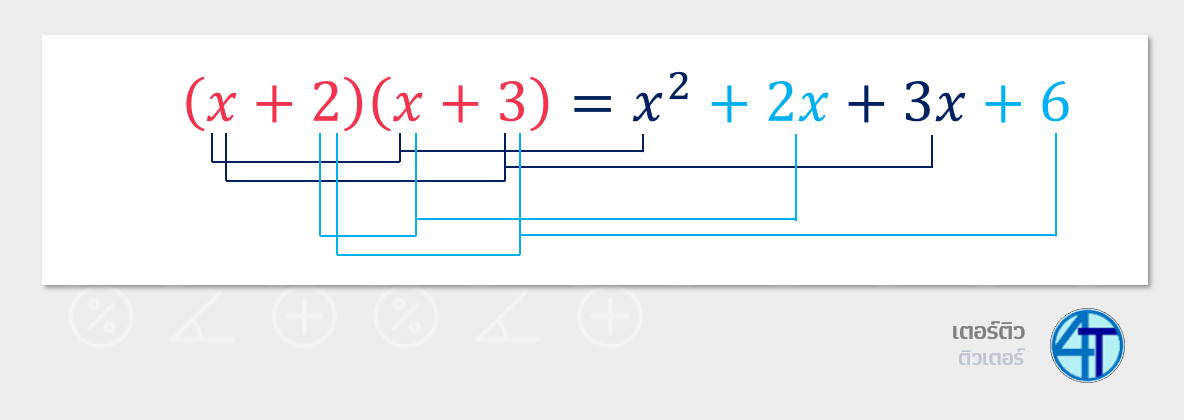
ตัวอย่างด้านบนคือตัวอย่างคร่าว ๆ ให้น้องเชื่อเฉย ๆ ว่า เออการคูณกลับ พจน์ \(x\) สองพจน์ จะได้ \(x^2\) ส่วนรายละเอียดเดี๋ยวเราไปดูกันในพาร์ทต่อไปกันได้เลย

การแยกตัวประกอบพหุนามดีกรีสองที่มีพจน์หน้า สปส.เป็น 1 (\(a=1\))

บทนี้พี่จะตบท้ายด้วยสมการหลายตัวแปรตามหลักสูตรในหนังสืออีกที ดังนั้นส่วนนี้เราจะเน้นแค่การแยกตัวประกอบแบบ ตัวแปรเดียว เน้น ๆ กันไปเลย ว่ามันมีทริคอะไรในการแยกตัวประกอบบ้าง

พหุนามดีกรีสองที่น้องจะเจอส่วนมากจะอยู่ในรูป \(ax^2+bx+c\) ซึ่ง เพื่อความง่ายเราจะพูดถึงตอนที่ \(a=1\) กันก่อน นั่นหมายความว่า เราจะแยกตัวประกอบของพหุนามดีกรีสอง แบบ \(x^2+bx+c\) นั่นเอง

หากน้องสังเกตจากภาพด้านล่าง จะเห็นว่า เวลาเราคูณกระจายกลับ (จับคูณทุกคู่เลยนะ 2 ตัว - 2 ตัว จับกันไปมา ได้ 4 คู่) พจน์ที่จะทำให้เกิด \(x^2\) มีแค่คู่พจน์แรกเท่านั้น ที่มี \(x\) และ \(x\) แต่พาร์ทนี้ เราสนใจแค่ \(x^2+bx+c\) หมายความว่า \(\textcolor{blue}{1}x^2+bx+c\) ดังนั้น วงเล็บหลังการแยกตัวประกอบหุนามดีกรีสองก็จะต้องเป็น \(1x\) และ \(1x\) ด้วย

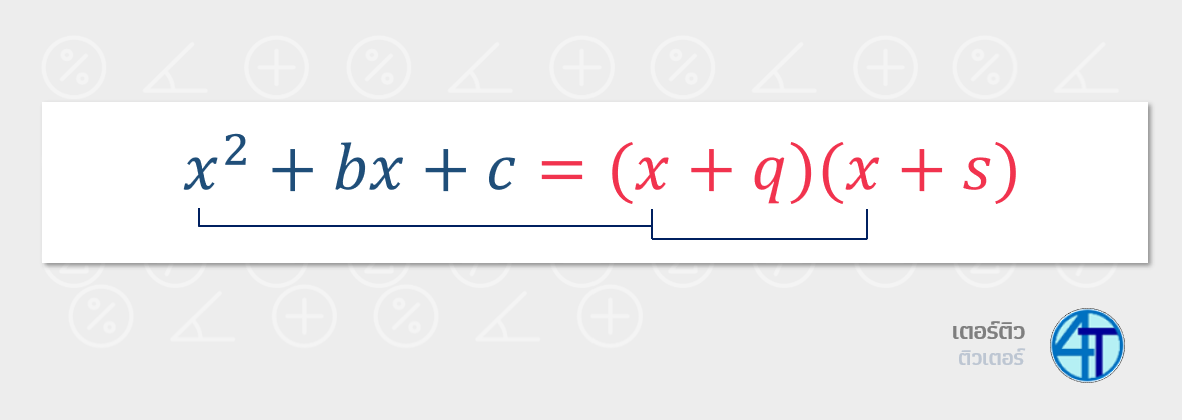
ดังนั้นหลังแยกตัวประกอบเราก็จะได้พหุนามหน้าตาประมาณนี้

ดังนั้น พี่ขอลองจับคู่กระจายตัวที่เหลือหน่อยและกันจะได้รู้ว่า \(q\) กับ \(s\) ควรจะมีค่าสัมพันธ์กับ \(b\) กับ \(c\) ที่โจทย์ให้ยังไง

ดังนั้นเรารู้และว่า หากคูณกระจายกลับเข้าไป \(q+s=b\) และ \(qs=c\) เป็นประโยคที่อาจารย์ชอบพูดกันว่า บวกกันได้ตัวกลาง คูณกันได้ตัวหลัง ที่มาจริง ๆ มันคือแบบนี้นี่แหละครับ

ดังนั้นก่อนจะงงกันไปมากกว่านี้ ลองไปดูโจทย์กันสักนิดนึง ก่อน สมมติพี่มี \(x^2+5x+6\) เราต้องการแยกตัวประกอบพหุนามนี้ เราก็ต้องคิดและว่า อะไรคูณกันได้ 6 บวกกันได้ 5 ซึ่งก็คือ \(2\) กับ \(3\) นั่นเอง เพราะ \(2+3=5\) และ \(2\times3=6\) ดังนั้น \(x^2+5x+6=(x+2)(x+3)\)

จากด้านบนทั้งหมดน้อง ๆ คงพอมองเห็นภาพว่า เราก็แค่ต้องหาเลขสองตัวที่คูณกันได้ตัวหลัง บวกกันได้ตรงกลาง แค่นี้เอง แล้วหากเราเจอพหุนามแบบนี้หล่ะ \(x^2-5x+4=0\) สังเกตว่ามันมีเครื่องหมายลบอยู่ข้างหน้า \(5x\) วิธีการคิดก็เหมือนเดิมครับน้อง บวกกันได้ตัวกลาง คูณกันได้ตัวหลัง แต่ตัวกลางในที่นี้ คือ \(-5\) นะ ไม่ใช่ \(5\) เฉย ๆ กล่าวง่าย ๆ คือให้น้องดึงเครื่องหมายติดมาด้วยนั่นเอง ดังนั้นข้อนี้ก็แค่หาว่า อะไรบวกกันได้ \(-5\) และคูณกันได้ \(4\) นั่นเอง คำตอบคือ \(-4\) กับ \(-1\) ดังนั้น \(x^2-5x+4=(x-4)(x-1)\)

อีกแบบที่จะเจอก็คือ \(x^2-2x-3\) เห้ยพี่ มันลบทั้งคู่เลย ไม่ต้องตกใจครับน้อง วิธีการเดิม บวกกันได้ตัวกลาง คูณกันได้ตัวหลัง ตัวกลางคือ \(-2\) ตัวหลังคือ \(-3\) บอกแล้วว่าดึงเครื่องหมายติดมาด้วย ดังนั้น เลขอะไรสองตัวที่คูณกันได้ \(-3\) และบวกกันได้ \(-2\) มันก็คือ \(-3\) กับ \(1\) นั่นเอง ดังนั้น \(x^2-2x-3=(x-3)(x+1)\) 

สังเกตกันได้เลยว่าเรื่อง แยกตัวประกอบพหุนามดีกรีสอง ไม่ได้ยาก (สำหรับกรณี \(a=0\) หรือ พจน์ \(x^2\) มีสัมประสิทธิ์เป็นหนึ่ง) มันเน้นการฝึกฝน เพราะสุดท้ายคำถามที่น้อง ๆ ต้องถามตัวเองคือ อะไรบวกกันได้ตัวกลาง คูณกันได้ตัวหลัง แค่นี้เอง แต่การหาเลขสองตัวที่ต้องการนี่แหละ คือปัญหาที่หลาย ๆ คน คิดช้า คิดเร็วแตกต่างกันไป ดังนั้น ใครสนใจวิธีและกระบวนการคิดแบบเป็นระบบ ว่าจะหาสองตัวเลขนี้ได้ยังไง สามารถกดดูคลิปวิดีโอด้านบนหน้านี้กันได้เลย พี่จะสอนเทคนิคการหาเลขสองตัวนี้เพิ่มเติม มันไม่ใช่วิธีลัดแต่อย่างใดแต่มันคือการหาเลขแบบเป็นระบบ

การแยกตัวประกอบแบบดีกรีสองรูปทั่วไป \(a\neq 1\)

พอ \(a\neq 1\) ชีวิตเราก็จะยากขึ้นไปเรื่อย ๆ ในพาร์ทนี้ เราจะมาดูตัวอย่างโจทย์และขั้นตอนทริคดี ๆ ในการหากัน (เตือนไว้ก่อนว่า การแยกตัวประกอบ ไม่มีวิธีลัดแบบแยกได้เร็ว ๆ สุดท้ายน้องก็ต้องไปคิดลองแทนหาตัวเลขที่เป็นไปได้อยู่ดี ดังนั้น บทนี้เน้นการฝึกฝนเป็นส่วนใหญ่ ถ้าถามว่า มีทริคมั้ย ก็มีนิดหน่อย ให้คิดได้เร็ว และไม่แทนตัวที่ไม่น่าใช่) ตามไปดูกันเลย

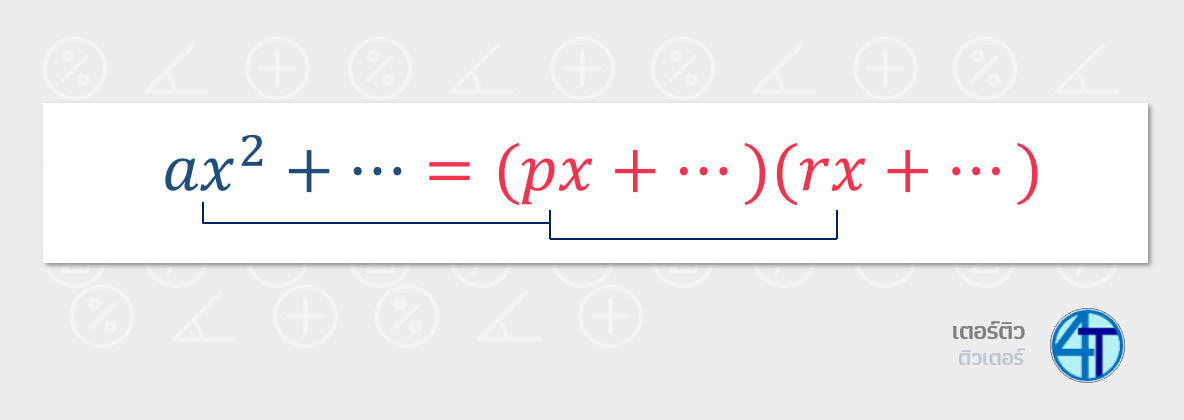
เรื่องนี้ให้น้องลืม บวกกันพจน์กลาง คูณกันพจน์หลัง ไปก่อนได้เลย เพราะมันมีพจน์หน้ามาเกี่ยวข้องด้วย ดังนั้น หลักการมันจะซับซ้อนกว่านิดนึง แต่ก็ไม่ได้ยากกว่ากันมากเท่าไหร่

ปัญหาเพิ่มมา คือ พจน์หน้ามี สปส. คือ \(a\) ดังนั้นมันไม่ใช่ \(1\) อีกต่อไปแล้ว เวลาเราแยกตัวประกอบออกมา มันก็จะติด \(p\) กับ \(r\) หน้าพจน์ \(x\) ด้วยเหมือนในรูปด้านบน (ฝั่งขวา) ดังนั้น แทนที่เราจะแยกตัวประกอบของพจน์หลังเพียงตัวเดียว (พูดถึงไปแล้วใน เทคนิคการหาเลขสองตัว พาร์ทบน) เพื่อลองแทนว่าคู่ไหนได้ เราก็ต้อง แยกตัวประกอบพจน์หน้าด้วย

ดังนั้น หลักการก็คือ แยกตัวประกอบทั้งหน้าและหลัง และลองแทนดูว่าเลขไหนใช้ได้ วันนี้พี่ก็มีเทคนิคมาฝากนิดนึงว่า ถ้าเลขไหนเป็น จำนวนเฉพาะ แปลว่าตัวประกอบมันจะมีแค่ 1 กับ ตัวมันเอง ดังนั้นเราควรทำตัวนี้ก่อน เพราะ มันมีกรณีเดียว

ตัวอย่างเช่น \(5x^2+13x+8=0\) สิ่งที่เราต้องทำคือ แยกตัวประกอบ \(5\) กับ \(8\) แต่ \(5\) เป็นจำนวนเฉพาะ ดังนั้น พี่ทำพจน์หน้าก่อน ได้ว่า \(5x^2+13x+8=(5x\dots)(x\dots)\) แน่ ๆ

ต่อมาพี่ก็จะแยกตัวประกอบพจน์หลัง เลข \(8\) ได้ว่า \(1, 2, 4, 8\) ดังนั้น จับคู่จะได้ \(1\times8\) กับ \(2\times4\) และเนื่องจากโจทย์ข้อนี้เป็น บวกทั้งหมด เราก็จะลองทำทีละคู่

คู่ 1 กับ 8 \((5x+1)(x+8)\) กับ \((5x+8)(x+1)\) น้องต้องสลับทั้งสองกรณีนะ และดูว่าใช่คำตอบหรือเปล่า อันแรก \((5x+1)(x+8)=5x^2+x+40x+8\) \(=5x^2+41x+8\)  ไม่ใช่ อันสอง \((5x+8)(x+1)=5x^2+8x+5x+8\) \(=5x^2+13x+8\) ถูกต้อง ก็เลยตอบได้เลย ไม่ต้องทำต่อ ว่า \(5x^2+13x+8=(5x+8)(x+1)\) 

กำลังสองสมบูรณ์

ให้น้องลองทำโจทย์ต่อไปนี้ และลองพิจารณาและสังเกตดูครับ

สังเกตกันหรือเปล่าว่า พหุนามข้างบนทั้งหมด เวลาเราแยกตัวประกอบกันออกมาแล้ว จะได้ พหุนามกำลังหนึ่ง ตัวเดียวกัน เช่น \((x+2)^2\) หรือ \((4x-1)^2\) อะไรประมาณนี้ เราจะเรียกพหุนามตั้งต้น (ดีกรีสอง) ว่า พหุนามกำลังสองสมบูรณ์ เนื่องจากมันแยกตัวประกอบ ได้เป็น อะไรสักอย่าง กำลังสอง นั่นเอง

ข้างบนเป็นสูตรที่น้องต้องจำได้ขึ้นใจเลยว่า หน้าบวกหลังกำลังสอง = หน้ากำลังสอง บวกสองหน้าหลัง บวกหลังกำลังสอง และ หน้าลบหลังกำลังสอง = หน้ากำลังสอง ลบสองหน้าหลัง บวกหลังกำลังสอง สังเกตดี ๆ สูตรมันคล้ายกันมาก ต่างแค่เครื่องหมายพจน์กลางเท่านั้นเอง

หากถามว่าแล้วสูตรนี้ใช้ทำอะไร สมมติน้อง มีพหุนาม \(x^2-6+9\) ถ้าพี่เขียนเป็น \(\textcolor{red}{x}^2-2\times\textcolor{red}{x}\times\textcolor{blue}{3}+\textcolor{blue}{3}^2\) มอง สีแดง เป็น หน้า และ สีน้ำเงิน เป็น หลัง เราก็จะได้ตามสูตร ซึ่งสูตรคือ หน้าลบหลังทั้งหมดกำลังสอง ดังนั้น มันก็คือ \(x^2-6+9=(\textcolor{red}{x}-\textcolor{blue}{3})^2\) 

ตัวอย่างโจทย์ แยกตัวประกอบของ \((x-2)^2+10(x-2)+25\)

(1) หากน้องทำตรงตัว เราต้องกระจายวงเล็บทั้งหมดก่อน \((x-2)^2+10(x-2)+25\) \(=(x^2-4x+4)+(10x-20)+25\)  ซึ่งรวมพจน์ทั้งหมดก็จะได้ \(x^2+6x+9\) จากนั้นก็แยกตัวประกอบได้ \((x+3)^2\)

(2) แต่หากเราสังเกตเห็นตั้งแต่แรกว่าโจทย์ข้อนี้อยู่ในรูปแบบ กำลังสองสมบูรณ์ มันจะง่ายขึ้นมากเลย ดังนี้ \(\textcolor{red}{(x-2)}^2+2\times\textcolor{red}{(x-2)}\times\textcolor{blue}{5}+\textcolor{blue}{5}^2\) เมื่อ หน้า คือ \((x-2)\) และ หลัง คือ \(5\) เราก็จะได้ว่า หน้าบวกหลังทั้งหมดกำลังสอง

\((\textcolor{red}{(x-2)}+\textcolor{blue}{5})^2=(x+3)^2\)

ผลต่างกําลังสอง

หากเรามีพจน์หน้ากับหลัง ทั้งคู่กำลังสองอยู่ เราสามารถใช้สูตรผลต่างกำลังสองเพื่อแยกตัวประกอบได้เลย เป็น หน้าบวกหลัง คูณ หน้าลบหลัง วิธีพิสูจน์ก็ไม่ยาก แค่กระจายฝั่งขวาสมการดู สมมติเรามี \((a+b)(a-b)\) \(=a^2+ab-ab+b^2=a^2-b^2\)  เพราะ \(ab\) มันตัดกันหายไป

ถ้าถามว่ามีประโยชน์อะไร ก็เหมือนเดิมครับน้อง ๆ ถ้าพหุนามที่น้องเจอมันอยู่ในรูป \(a^2-b^2\) ก็ให้น้องใช้สูตรได้เลย เช่น

โจทย์ถามว่า จงแยกตัวประกอบของ \(25x^2-9\) แบบนี้จะไปทำวิธีปกติในเรื่อง แยกตัวประกอบดีกรีสองเมื่อ \(a\neq 1\) ก็ได้ แต่เสียเวลา เพราะเราเห็นแล้วว่า \(25x^2=(5x)^2\) และ \(9=3^2\) ดังนั้นสมการด้านบนพี่เขียนใหม่ได้เป็น \(\textcolor{red}{(5x)}^2-\textcolor{blue}{3}^2=(\textcolor{red}{5x}+\textcolor{blue}{3})(\textcolor{red}{5x}-\textcolor{blue}{3})\) ตอบจบ

การแยกตัวประกอบโดยใช้สมบัติการแจกแจง

พาร์ทนี้พี่ขอไม่ลงลึก แต่มันมีในหลักสูตร ดังนั้น จะกล่าวสั้น ๆ เฉย ๆ ว่า การแยกตัวประกอบแบบนี้ คือการดึงตัวร่วม นั่นเอง ตัวอย่างโจทย์ ในกรณีที่ตัวแปรไม่ใช่ตัวเดียว เช่น \(12x^2y-9xy^2\) แบบนี้

จากโจทย์ข้างบน หากสังเกตกันดี ๆ จะเห็นว่า พจน์หน้า กับ พจน์หลัง มี \(3\) เป็นตัวร่วม เพราะ ห.ร.ม. ของ \(9\) กับ \(12\) คือ \(3\) ดังนั้น เราดึงสามออกมาได้ เป็น \(12x^2y-9xy^2=3(4x^2y-3xy^2)\) หากสังเกตต่อไปอีก น้องจะเห็นว่า ทั้งสองพจน์มี \(x\) อย่างน้อย 1 ตัว เพราะ พจน์หน้า \(x^2\) คือมี \(x\) 2 ตัว และพจน์หลัง มี \(x\) ตัวเดียว ดังนั้น ตัวร่วมอีกอันคือ \(x\) หากดึง \(x\) ก็จะได้ \(3(4x^2y-3xy^2)=3x(4xy-3y^2)\) ยังไม่จบ เพราะ \(y\) ก็เป็นตัวร่วมเหมือนกัน เราก็ดึง \(y\) จะได้ \(3x(4xy-3y^2)=3xy(4x-3y)\) สังเกตว่า ตัวร่วมหมดแล้ว

ดังนั้น เราก็จะได้ว่า \(12x^2y-9xy^2=3xy(4x-3y)\) 

ส่วนนี้เอาจริง ๆ เป็นพื้นฐานที่น้องจะต้องใช้และดึงตัวร่วมให้คล่อง เวลาไปเจอโจทย์ข้อสอบ เราจะใช้การดึงตัวร่วมแบบแก้สมการ (แบบยาก) ดังนั้น เรื่องนี้ก็เป็นพื้นฐานสำคัญเหมือนกันครับ ที่น้องต้องทำเป็น เวลาเอาไปแก้สมการ

คำถามที่ต้องถามตัวเองในหัวคือ เวลาเจอพหุนาม บวกลบ กัน มันมีตัวร่วมอะไรให้เราดึงได้หรือเปล่า